Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Expliquer ce qu’est une distribution de charges de source continue et comment elle est liée au concept de quantification de la charge
- Décrire les charges linéaires, les charges de surface et les charges de volume
- Calculer le champ d’une distribution de charges de source continue de l’un ou l’autre signe
Les distributions de charges que nous avons vues jusqu’à présent étaient discrètes : composées de particules ponctuelles individuelles. Ceci est en contraste avec une distribution de charge continue, qui a au moins une dimension non nulle. Si une distribution de charge est continue plutôt que discrète, nous pouvons généraliser la définition du champ électrique. Nous divisons simplement la charge en morceaux infinitésimaux et traitons chaque morceau comme une charge ponctuelle.
Notez que parce que la charge est quantifiée, il n’existe pas de distribution de charge « vraiment » continue. Cependant, dans la plupart des cas pratiques, la charge totale créant le champ implique un nombre si énorme de charges discrètes que nous pouvons sans risque ignorer la nature discrète de la charge et la considérer comme continue. C’est exactement le genre d’approximation que nous faisons lorsque nous traitons un seau d’eau comme un fluide continu, plutôt que comme une collection de \(\ce{H2O}\) molécules.
Notre première étape consiste à définir une densité de charge pour une distribution de charge le long d’une ligne, sur une surface ou dans un volume, comme le montre la figure \(\PageIndex{1}\).
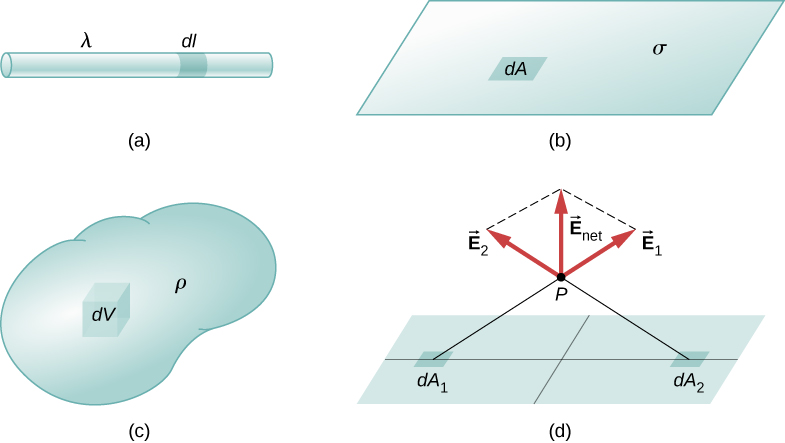
Définitions : Densités de charge
Définitions de la densité de charge :
- Densité de charge linéaire : \(\lambda \equiv \) charge par unité de longueur (Figure \(\PageIndex{1a}\)) ; les unités sont des coulombs par mètre (\(C/m\))
- Densité de charge de surface : \(\sigma \equiv \) charge par unité de surface (Figure \(\PageIndex{1b}\)) ; les unités sont des coulombs par mètre carré \((C/m^2)\)
- Densité de charge volumique : \(\rho \equiv \) charge par unité de volume (Figure \(\PageIndex{1c}\)) ; les unités sont des coulombs par mètre carré ; \((C/m^3)\)
Pour une charge linéaire, une charge de surface et une charge de volume, la sommation dans la définition d’un champ électrique discutée précédemment devient une intégrale et \(q_i\) est remplacée par \(dq = \lambda dl\), \(\sigma dA\), ou \(\rho dV\), respectivement :
\ \vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right) \hat{r}}_{\text{\}Line charge}} \label{eq2} &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{surface} \left(\dfrac{\sigma \,dA}{r^2}\right) \hat{r} }_{\text{Surface charge}}\label{eq3} \\\N- \N-vec{E}(P) &= \N-underbrace{\N{\i1}{4\pi \epsilon_0} \int_{volume} \left(\dfrac{\rho \,dV}{r^2}\right) \hat{r}}_{\text{{Volume charge}} \label{eq4} \end{align}\]
Les intégrales des équations \ref{eq1}-\ref{eq4} sont des généralisations de l’expression du champ d’une charge ponctuelle. Elles incluent et supposent implicitement le principe de superposition. Le « truc » pour les utiliser consiste presque toujours à trouver des expressions correctes pour \(dl\), \(dA\), ou \(dV\), selon le cas, exprimées en fonction de r, et à exprimer également la fonction de densité de charge de manière appropriée. Elle peut être constante ; elle peut dépendre de l’emplacement.
Notez soigneusement la signification de \(r\) dans ces équations : C’est la distance entre l’élément de charge (\(q_i, \, \lambda \, dl, \, \sigma \, dA, \, \rho \, dV\)) et l’emplacement d’intérêt, \(P(x, y, z)\). (le point dans l’espace où vous voulez déterminer le champ). Cependant, ne confondez pas cela avec la signification de \(\hat{r}\) ; nous l’utilisons ainsi que la notation vectorielle \(\vec{E}\) pour écrire trois intégrales à la fois. C’est-à-dire que l’équation \ref{eq2} est en fait
\ E_y(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right)_y, \\\\ E_z(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right)_z \end{align} \]
Exemple \(\PageIndex{1}\) : Champ électrique d’un segment de ligne
Trouvez le champ électrique à une distance \(z\) au-dessus du point médian d’un segment de ligne droite de longueur \(L\) qui porte une densité de charge linéaire uniforme \(\lambda\).
Stratégie
Comme il s’agit d’une distribution de charge continue, nous décomposons conceptuellement le segment de fil en morceaux différentiels de longueur \(dl\), dont chacun porte une quantité différentielle de charge
Puis, nous calculons le champ différentiel créé par deux morceaux de fil placés symétriquement, en utilisant la symétrie de la configuration pour simplifier le calcul (figure \(\PageIndex{2}\)). Enfin, nous intégrons cette expression de champ différentiel sur la longueur du fil (la moitié, en fait, comme nous l’expliquons ci-dessous) pour obtenir l’expression complète du champ électrique.
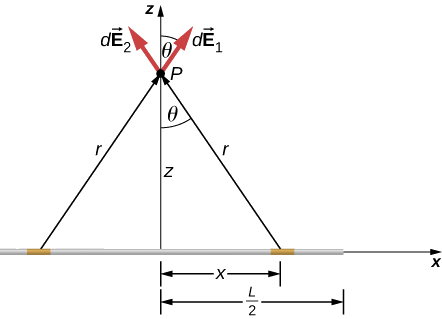
Solution
Avant de nous lancer, à quoi le champ doit-il » ressembler » de loin ? Comme il s’agit d’un segment de ligne fini, de loin, il devrait ressembler à une charge ponctuelle. Nous allons vérifier l’expression que nous obtenons pour voir si elle répond à cette attente.
Le champ électrique pour une charge linéaire est donné par l’expression générale
La symétrie de la situation (notre choix des deux morceaux différentiels identiques de charge) implique que les composantes horizontales (x) du champ s’annulent, de sorte que le champ net pointe dans la direction \(z\). Vérifions cela formellement.
Le champ total \(\vec{E}(P)\) est la somme vectorielle des champs de chacun des deux éléments de charge (appelons-les \(\vec{E}_1\) et \(\vec{E}_2\), pour le moment):
&= E_{1x}\hat{i} + E_{1z}\hat{k} + E_{2x} (-\hat{i}) + E_{2z}\hat{k}. \end{align*}\]
Parce que les deux éléments de charge sont identiques et sont à la même distance du point \(P\) où l’on veut calculer le champ, \(E_{1x} = E_{2x}\), ces composantes s’annulent. Il reste donc
&= E_1 \, \cos \, \theta \hat{k} + E_2 \, \cos \, \theta \hat{k}.
Ces composantes sont également égales, on a donc
&= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda dx}{r^2} \, \cos \, \theta \hat{k} \end{align*}\]
où notre élément de ligne différentielle dl est dx, dans cet exemple, puisque nous intégrons le long d’une ligne de charge qui se trouve sur l’axe des x. (Les limites de l’intégration sont 0 à \(\frac{L}{2}\), et non \(-\frac{L}{2}\) à \(+\frac{L}{2}\), parce que nous avons construit le champ net à partir de deux éléments différentiels de charge \(dq\). Si nous intégrions sur toute la longueur, nous prendrions un facteur erroné de 2.)
En principe, ceci est complet. Cependant, pour calculer réellement cette intégrale, nous devons éliminer toutes les variables qui ne sont pas données. Dans ce cas, à la fois \(r\) et \(\theta\) changent lorsque nous intégrons vers l’extérieur jusqu’à la fin de la charge linéaire, ce sont donc les variables dont il faut se débarrasser. Nous pouvons le faire de la même manière que pour les deux charges ponctuelles : en remarquant que
et
En substituant, nous obtenons
&= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda z}{(z^2 + x^2)^{3/2} dx \hat{k} \\N &= \dfrac{2 \lambda z}{4 \pi \epsilon_0} \left_0^{L/2} \hat{k}. \end{align*}]
ce qui se simplifie en
Signification
Notez, une fois de plus, l’utilisation de la symétrie pour simplifier le problème. C’est une stratégie très courante pour calculer les champs électriques. Les champs de distributions de charges non symétriques doivent être traités avec de multiples intégrales et peuvent avoir besoin d’être calculés numériquement par un ordinateur.
Exercice \(\PageIndex{1}\)
Comment la stratégie utilisée ci-dessus changerait-elle pour calculer le champ électrique en un point situé à une distance \(z\) au-dessus d’une extrémité du segment de droite fini ?
Réponse
Nous ne pourrons plus profiter de la symétrie. Au lieu de cela, nous devrons calculer chacune des deux composantes du champ électrique avec leur propre intégrale.
Exemple \(\PageIndex{2}\) : Champ électrique d’une ligne de charge infinie
Trouver le champ électrique à une distance \(z\) au-dessus du point médian d’une ligne de charge infinie qui porte une densité de charge linéaire uniforme \(\lambda\).
Stratégie
C’est exactement comme l’exemple précédent, sauf que les limites d’intégration seront \(-\infty\) à \(+\infty\).
Solution
Encore, les composantes horizontales s’annulent, donc nous nous retrouvons avec
où notre élément de ligne différentielle dl est dx, dans cet exemple, puisque nous intégrons le long d’une ligne de charge qui se trouve sur l’axe des x. Encore une fois,
\N &= \dfrac{z}{(z^2 + x^2)^{1/2}}. \end{align*}
En substituant, on obtient
&= \dfrac{1}{4 \pi \epsilon_0} \int_{-\infty}^{\infty} \dfrac{\lambda z}{(z^2 + x^2)^{3/2}dx \hat{k} &= \dfrac{1}{4 \pi \epsilon_0} \left_{-\infty}^{\infty} \, \hat{k} \end{align*}\]
ce qui se simplifie en
Signification
Notre stratégie pour travailler avec des distributions de charges continues donne également des résultats utiles pour les charges de dimension infinie.
Dans le cas d’une ligne de charge finie, notez que pour \(z \gg L\), \(z^2\) domine le L dans le dénominateur, de sorte que l’équation \ref{5.12} se simplifie en
Si l’on se rappelle que \(\lambda L = q\) la charge totale sur le fil, nous avons retrouvé l’expression du champ d’une charge ponctuelle, comme prévu.
Dans la limite \(L \lambda L = q\) par contre, nous obtenons le champ d’un fil droit infini, c’est-à-dire un fil droit dont la longueur est beaucoup, beaucoup plus grande que l’une ou l’autre de ses autres dimensions, et aussi beaucoup, beaucoup plus grande que la distance à laquelle le champ doit être calculé :
Un artefact intéressant de cette limite infinie est que nous avons perdu la dépendance habituelle \(1/r^2\) à laquelle nous sommes habitués. Cela deviendra encore plus intriguant dans le cas d’un plan infini.
Exemple \(\PageIndex{3A}\) : Champ électrique dû à un anneau de charge
Un anneau a une densité de charge uniforme \(\lambda\), avec des unités de coulomb par unité de mètre d’arc. Trouvez le champ électrique en un point de l’axe passant par le centre de l’anneau.
Stratégie
Nous utilisons la même procédure que pour le fil chargé. La différence ici est que la charge est répartie sur un cercle. Nous divisons le cercle en éléments infinitésimaux en forme d’arcs sur le cercle et utilisons les coordonnées polaires indiquées sur la figure \(\PageIndex{3}\).
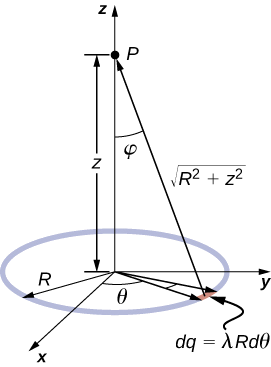
Solution
Le champ électrique d’une charge linéaire est donné par l’expression générale
Un élément général de l’arc entre \(\theta\) et \(\theta + d\theta\) est de longueur \(Rd\theta\) et contient donc une charge égale à \(\lambda R \,d\theta\). L’élément est à une distance de \(r = \sqrt{z^2 + R^2}\) de \(P\), l’angle est \(\cos \, \phi = \dfrac{z}{\sqrt{z^2+R^2}}\) et donc le champ électrique est
\ &= \dfrac{1}{4\pi \epsilon_0} \dfrac{\lambda Rz}{(z^2 + R^2)^{3/2}} \hat{z} \int_0^{2\pi} d\theta \\\N &= \dfrac{1}{4\pi \epsilon_0} \dfrac{2\pi \lambda Rz}{(z^2 + R^2)^{3/2}} \hat{z} \\N &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}} \hat{z}. \end{align*}\]
Signification
Comme d’habitude, la symétrie a simplifié ce problème, aboutissant dans ce cas particulier à une intégrale triviale. De plus, lorsqu’on prend la limite de \(z \gg R\), on trouve que
comme on s’y attend.
Exemple \(\PageIndex{3B}\) : Le champ d’un disque
Trouve le champ électrique d’un disque circulaire mince de rayon \(R\) et de densité de charge uniforme à une distance \(z\) au-dessus du centre du disque (Figure \(\PageIndex{4}\))
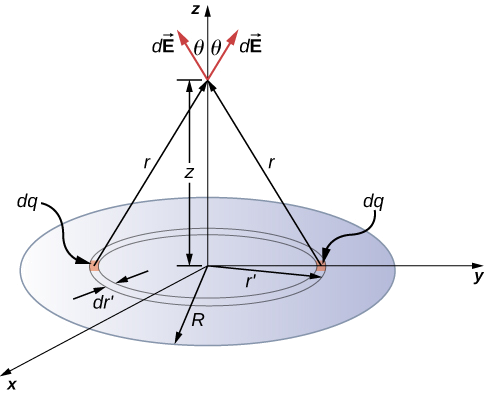
Stratégie
Le champ électrique pour une charge de surface est donné par
Pour résoudre les problèmes de charge de surface, nous brisons la surface en » bandes » différentielles symétriques qui correspondent à la forme de la surface ; ici, nous utiliserons des anneaux, comme le montre la figure. Là encore, par symétrie, les composantes horizontales s’annulent et le champ est entièrement orienté dans la direction verticale \((\hat{k})\). La composante verticale du champ électrique est extraite en multipliant par \(\theta\), donc
Comme précédemment, nous devons réécrire les facteurs inconnus dans l’intégrande en termes de quantités données. Dans ce cas,
(Notez bien les deux « \(r\) » différents ici ; \(r\) est la distance entre l’anneau différentiel de charge et le point \(P\) où nous souhaitons déterminer le champ, tandis que \(r’\) est la distance entre le centre du disque et l’anneau différentiel de charge). De plus, nous avons déjà effectué l’intégrale de l’angle polaire en écrivant \(dA\).
Solution
En substituant tout cela, on obtient
\ &= \dfrac{1}{4 \pi \epsilon_0}. \int_0^R \dfrac{\sigma (2\pi r’ dr’)z}{(r’^2 + z^2)^{3/2}} \hat{k} \\N &= \dfrac{1}{4 \pi \epsilon_0} (2\pi \sigma z)\left(\dfrac{1}{z} – \dfrac{1}{\sqrt{R^2 + z^2}}\right) \hat{k} \end{align*}\]
ou, plus simplement,
Signification
Encore, on peut montrer (via une expansion de Taylor) que lorsque \(z \gg R\), cela se réduit à
ce qui est l’expression pour une charge ponctuelle \(Q = \sigma \pi R^2\).
Exercice \(\PageIndex{3}\)
Comment la limite ci-dessus changerait-elle avec un rectangle uniformément chargé au lieu d’un disque ?
Réponse
La charge ponctuelle serait \(Q = \sigma ab\) où \(a\) et \(b\) sont les côtés du rectangle mais autrement identiques.
Comme \(R \rightarrow \infty\), l’équation \ref{5.14} se réduit au champ d’un plan infini, qui est une feuille plane dont l’aire est beaucoup, beaucoup plus grande que son épaisseur, et aussi beaucoup, beaucoup plus grande que la distance à laquelle on veut calculer le champ :
&= \dfrac{\sigma}{2 \epsilon_0} \hat{k}. \label{5.15} \end{align}\]
Notez que ce champ est constant. Ce résultat surprenant est, encore une fois, un artefact de notre limite, bien que nous l’utiliserons à plusieurs reprises à l’avenir. Pour comprendre pourquoi cela se produit, imaginez que vous êtes placé au-dessus d’un plan infini de charge constante. L’avion semble-t-il différent si vous variez votre altitude ? Non, vous voyez toujours l’avion s’éloigner à l’infini, quelle que soit la distance qui vous sépare de lui. Il est important de noter que l’équation \ref{5.15} s’applique parce que nous sommes au-dessus du plan. Si nous étions en dessous, le champ serait orienté dans la direction \(- \hat{k}\).
Exemple \(\PageIndex{4}\) : Le champ de deux plans infinis
Trouve le champ électrique partout résultant de deux plans infinis avec des densités de charge égales mais opposées (figure \(\PageIndex{5}\)).
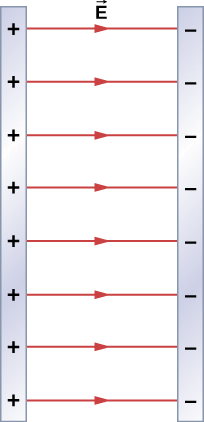
Stratégie
Nous connaissons déjà le champ électrique résultant d’un seul plan infini, nous pouvons donc utiliser le principe de superposition pour trouver le champ de deux.
Solution
Le champ électrique s’éloigne du plan chargé positivement et se dirige vers le plan chargé négativement. Comme les \(\sigma\) sont égaux et opposés, cela signifie que dans la région située à l’extérieur des deux plans, les champs électriques s’annulent jusqu’à zéro. Cependant, dans la région située entre les plans, les champs électriques s’additionnent, et nous obtenons
pour le champ électrique. Le \(\hat{i}\) est dû au fait que dans la figure, le champ pointe dans la direction +x.
Signification
Les systèmes qui peuvent être approximés comme deux plans infinis de ce type fournissent un moyen utile de créer des champs électriques uniformes.
Exercice \(\PageIndex{4}\)
À quoi ressemblerait le champ électrique dans un système comportant deux plans parallèles chargés positivement avec des densités de charge égales ?
Réponse
Le champ électrique serait nul entre les deux, et aurait une magnitude \(\dfrac{\sigma}{\epsilon_0}\) partout ailleurs.
Contributeurs et attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) et Bill Moebs avec de nombreux auteurs collaborateurs. Ce travail est autorisé par OpenStax University Physics sous une licence Creative Commons Attribution License (by 4.0).
.