
Dans un article précédent, nous avons exploré l’analyse de régression linéaire et son application en analyse et modélisation financière. Vous pouvez lire notre article L’analyse de régression dans la modélisation financière pour avoir un meilleur aperçu des concepts statistiques employés dans la méthode et où elle trouve son application dans la finance.
Cet article va jeter un regard pratique sur la modélisation d’un modèle de régression multiple pour le produit intérieur brut (PIB) d’un pays.
Avant de commencer, permettez-moi d’ajouter un bref avertissement. Je ne suis pas un statisticien, et je ne prétends pas que les variables dépendantes et indépendantes sélectionnées sont les bons choix d’analyse. Cet article a pour but de vous montrer comment exécuter une régression multiple dans Excel et interpréter les résultats, et non d’enseigner la mise en place des hypothèses de notre modèle et le choix des variables les plus appropriées.
Maintenant que ce point est acquis et que les attentes sont fixées, ouvrons Excel et commençons !
Nous allons obtenir des données publiques d’Eurostat, la base de données statistiques de la Commission européenne pour cet exercice. Toutes les données sources pertinentes se trouvent dans le fichier modèle pour votre commodité, que vous pouvez télécharger ci-dessous. J’ai également conservé les liens vers les tableaux sources pour les explorer davantage si vous le souhaitez.
L’ensemble de données de l’UE nous donne des informations pour tous les États membres de l’union. En tant que fan massif d’Hercule Poirot d’Agatha Christie, dirigeons notre attention sur la Belgique.
Comme vous pouvez le voir dans le tableau ci-dessous, nous avons dix-neuf observations de notre variable cible (PIB), ainsi que nos trois variables prédictives :
- X1 – Dépenses d’éducation en mil.;
- X2 – Taux de chômage en % de la population active ;
- X3 – Rémunération des employés en mil.

Avant même d’exécuter notre modèle de régression, nous remarquons certaines dépendances dans nos données. En regardant l’évolution au cours des périodes, nous pouvons supposer que le PIB augmente en même temps que les dépenses d’éducation et la rémunération des employés.
Exécution d’une régression linéaire multiple
Il existe des moyens de calculer toutes les statistiques pertinentes dans Excel en utilisant des formules. Mais c’est beaucoup plus facile avec le pack d’outils d’analyse de données, que vous pouvez activer à partir de l’onglet Développeur -> Compléments Excel.
Regardez l’onglet Données, et sur la droite, vous verrez l’outil d’analyse de données au sein de la section Analyser.
Lancez-le et choisissez Régression parmi toutes les options. Notez, nous utilisons le même menu pour les modèles de régression linéaire simple (unique) et multiple.
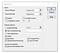
Maintenant, il est temps de définir quelques plages et paramètres.
La plage Y comprendra notre variable dépendante, le PIB. Et dans la plage X, nous allons sélectionner toutes les colonnes de la variable X. S’il vous plaît, notez que c’est la même chose que d’exécuter une régression linéaire unique, la seule différence étant que nous choisissons plusieurs colonnes pour la Plage X.
N’oubliez pas qu’Excel exige que toutes les variables X soient dans des colonnes adjacentes.
Comme j’ai sélectionné la colonne Titres, il est crucial de cocher la case pour Étiquettes. Un intervalle de confiance de 95 % est approprié dans la plupart des scénarios d’analyse financière, nous ne le modifierons donc pas.
Vous pouvez ensuite envisager de placer les données sur la même feuille ou sur une nouvelle. Une nouvelle feuille de travail fonctionne généralement mieux, car l’outil insère pas mal de données.
Je vais également marquer toutes les options supplémentaires en bas. Je finis rarement par toutes les utiliser, mais il est plus facile de supprimer celles dont nous n’avons pas besoin que de réexécuter l’ensemble.
.
S’inscrire à notre Newsletter pour obtenir un modèle GRATUIT d’analyse comparative Excel
Évaluation des résultats de la régression
Maintenant que nous avons notre sortie résumée d’Excel, explorons davantage notre modèle de régression.
Les informations que nous avons obtenues du module d’analyse de données d’Excel commencent par les statistiques de régression.
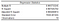
Le carré R est le plus important d’entre eux, donc nous pouvons commencer par l’examiner. Plus précisément, nous devrions examiner le R² ajusté dans notre cas, car nous avons plus d’une variable X. Il nous donne une idée de l’ensemble des résultats. Il nous donne une idée de la qualité globale de l’ajustement.
Un R carré ajusté de 0,98 signifie que notre modèle de régression peut expliquer environ 98 % de la variation de la variable dépendante Y (PIB) autour de la valeur moyenne des observations (la moyenne de notre échantillon). En d’autres termes, 98 % de la variabilité de ŷ (y-hat, les prédictions de notre variable dépendante) est capturée par notre modèle. Une valeur aussi élevée indique généralement que notre modèle pourrait présenter un problème. Nous allons continuer avec notre modèle, mais un R Squared trop élevé peut être problématique dans un scénario de la vie réelle. Je vous suggère de lire cet article sur Statistics by Jim, pour apprendre pourquoi trop bon n’est pas toujours bon en termes de R Carré.
L’erreur standard nous donne une estimation de l’écart type de l’erreur (résidus). En général, si le coefficient est important par rapport à l’erreur standard, il est probablement statistiquement significatif.
Analyse de la variance (ANOVA)

.
La section Analyse de la variance est quelque chose que nous sautons souvent lors de la modélisation de la régression. Cependant, elle peut fournir des informations précieuses, et cela vaut la peine d’y jeter un coup d’œil. Vous pouvez en savoir plus sur l’exécution d’un test ANOVA et voir un exemple de modèle dans notre article dédié.
Ce tableau nous donne un test global de signification sur les paramètres de régression.
La colonne F du tableau ANOVA nous donne le test F global de l’hypothèse nulle selon laquelle tous les coefficients sont égaux à zéro. L’hypothèse alternative est qu’au moins un des coefficients n’est pas égal à zéro. La colonne F de signification nous indique la valeur p du test F. Comme elle est inférieure au niveau de signification, la valeur p est inférieure à la valeur du test. Comme elle est inférieure au niveau de signification de 0,05 (au niveau de confiance choisi de 95 %), nous pouvons rejeter l’hypothèse nulle, à savoir que tous les coefficients sont égaux à zéro. Cela signifie que nos paramètres de régression ne sont conjointement pas statistiquement insignifiants.
Vous pouvez en savoir plus sur les tests d’hypothèse dans notre article dédié.
Le tableau suivant nous donne des informations sur les coefficients de notre modèle de régression multiple et constitue la partie la plus passionnante de l’analyse.

.
Nous avons ici de nombreux détails pour l’intercept et chacune de nos prédicteurs (variables indépendantes). Explorons ce que représentent ces colonnes :
- Coefficients – ce sont des estimations dérivées par la méthode des moindres carrés;
- Erreur standard – l’écart type des estimations des moindres carrés ;
- T-Stat – il s’agit de la statistique t pour l’hypothèse nulle que le coefficient est égal à zéro, par rapport à l’hypothèse alternative qu’il est différent de zéro;
- La valeur P pour le test t;
- Les 95% inférieur et supérieur définissent l’intervalle de confiance pour les coefficients.
Test de signification statistique
C’est le test d’une hypothèse nulle affirmant que le coefficient a une pente de zéro. Nous pouvons regarder les valeurs p pour chaque coefficient et les comparer au niveau de signification de 0,05.
Si notre valeur p est inférieure au niveau de signification, cela signifie que notre variable indépendante est statistiquement significative pour le modèle. En examinant nos prédicteurs X1 à X3, nous remarquons que seul X3 Rémunération des employés a une valeur p inférieure à 0,05, ce qui signifie que X1 Dépenses d’éducation et X2 Taux de chômage ne semblent pas être statistiquement significatifs pour notre modèle de régression.
Comme nous ne pouvons pas rejeter l’hypothèse nulle (que les coefficients sont égaux à zéro), nous pouvons éliminer X1 et X2 du modèle. Nous pouvons également le confirmer car la valeur zéro se situe entre les intervalles de confiance inférieur et supérieur.
Nous pouvons décider d’exécuter le modèle sans les variables X1 et X2 et évaluer si cela entraîne une baisse significative de la mesure du R carré ajusté. Si ce n’est pas le cas, alors il est sûr de laisser tomber X1 et X2 du modèle de régression.
Si nous faisons cela, nous obtenons les statistiques de régression suivantes.

Nous pouvons voir qu’il n’y a pas de baisse du R Square, donc nous pouvons en toute sécurité supprimer X1 et X2 de notre modèle et le simplifier à une seule régression linéaire.
Sortie résiduelle
Les résidus donnent des informations sur la mesure dans laquelle les points de données réels (y) s’écartent des points de données prédits (ŷ), sur la base de notre modèle de régression.

Sortie de la probabilité
Ce tableau présente les valeurs observées pour la variable indépendante (y) et les percentiles d’échantillon correspondants. Nous pouvons calculer le premier percentile comme (100 / 2 * Nombre d’observations), et à partir de là, ceux-ci sont calculés comme le percentile précédent + (100 / 2).

Plots des résidus
L’analyse de régression multiple nous donne un graphique pour chaque variable indépendante par rapport aux résidus. Nous pouvons utiliser ces tracés pour évaluer si les données de notre échantillon correspondent aux hypothèses de linéarité et d’homogénéité de la variance.
L’homogénéité signifie que le tracé doit présenter un modèle aléatoire et avoir un écart vertical constant.
La linéarité exige que les résidus aient une moyenne de zéro. Nous pouvons l’observer visuellement en évaluant si les points sont répartis à peu près également en dessous et au-dessus de l’axe des x.



Line Fit Plots
Le modèle nous fournit un Line Fit Plot pour chaque variable indépendante (prédicteur). Celui-ci montre les valeurs prédites (ŷ) par rapport aux valeurs observées (y). Plus celles-ci correspondent, mieux notre modèle prédit la variable dépendante sur la base des régresseurs.



Plot de probabilité normale
Le plot de probabilité normale nous aide à déterminer si les données correspondent à une distribution normale. Nous pouvons ajouter une ligne de tendance et évaluer si les points de données suivent une ligne droite. Dans notre cas, cela est assez évident, et nous pouvons même ne pas ajouter la ligne de tendance.

.
Vous pouvez télécharger l’exemple de modèle sous Excel dans l’article original.
Limites d’Excel
Comme Excel n’est pas un logiciel de statisticien spécialisé, il y a quelques limites inhérentes à l’exécution d’un modèle de régression dont nous devons être conscients :
- Les colonnes de tous les régresseurs (variables indépendantes) doivent être adjacentes;
- Nous pouvons avoir jusqu’à 16 prédicteurs (je ne me souviens plus où j’ai lu cela, donc à prendre avec précaution) ;
- L’analyse de régression dans Excel suppose que l’erreur est indépendante avec une variance constante (homoscédasticité);
- Si nous empruntons la voie des fonctions, il est crucial de savoir que les fonctions Excel SLOPE, INTERCEPT et FORECAST ne fonctionnent pas pour la régression multiple. En revanche, TREND et LINEST fonctionnent de la même manière qu’avec un modèle de régression unique mais prennent des valeurs pour plusieurs variables X.
Conclusion
Nous avons commencé avec trois variables indépendantes, effectué une analyse de régression et identifié que deux prédicteurs n’ont pas de signification statistique pour notre modèle.
Nous avons alors éliminé celles-ci pour aboutir à un modèle de régression linéaire simple.
Une fois que vous êtes satisfait de votre modèle, vous pouvez construire votre équation de régression, comme nous l’avons abordé dans d’autres articles. Avec cette équation, vous pouvez alors prévoir la variable dépendante pour le futur.
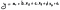
Où :
- y est notre variable dépendante;
- a est l’ordonnée à l’origine (notre constante) des statistiques de régression;
- b, c et d sont les coefficients de chaque variable;
- x1 à x3 sont les variables indépendantes (nos régresseurs ou prédicteurs);
- ɛ est l’erreur ou les résidus, que nous pouvons souvent exclure.
Ne perdez pas de vue que cet article vise à illustrer les concepts d’exécution d’une analyse de régression multiple dans Excel. Il tente d’expliquer ce sur quoi nous devons nous concentrer lors de l’évaluation des résultats. Chaque bon modèle commence par la définition d’hypothèses et d’attentes raisonnables, dont je ne suis pas un expert, et je ne prétends donc pas que les variables dépendantes et indépendantes choisies étaient les bons choix.
Merci de votre lecture ! Vous pouvez montrer votre soutien en partageant cet article avec des collègues et des amis.
Les résultats de l’étude de cas sont présentés dans le tableau ci-dessous.