Afficher l’avis de mobile Afficher toutes les notes Cacher toutes les notes
Section 1-12 : Coordonnées cylindriques
Comme pour l’espace à deux dimensions, le système de coordonnées standard \(\left( {x,y,z} \right)\) est appelé le système de coordonnées cartésiennes. Dans les deux dernières sections de ce chapitre, nous allons étudier d’autres systèmes de coordonnées pour l’espace à trois dimensions.
Nous allons commencer par le système de coordonnées cylindriques. Celui-ci est assez simple puisqu’il n’est rien d’autre qu’une extension des coordonnées polaires en trois dimensions. Non seulement c’est une extension des coordonnées polaires, mais nous l’étendons dans la troisième dimension tout comme nous étendons les coordonnées cartésiennes dans la troisième dimension. Tout ce que nous faisons, c’est ajouter une \(z\) sur comme troisième coordonnée. Les \(r\) et \(\theta\) sont les mêmes que pour les coordonnées polaires.
Voici le croquis d’un point dans \({\mathbb{R}^3}\).
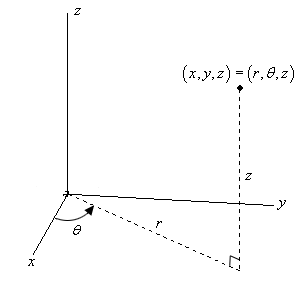
Les conversions pour \(x\) et \(y\) sont les mêmes conversions que nous avons utilisées à l’époque où nous regardions les coordonnées polaires. Ainsi, si nous avons un point en coordonnées cylindriques, les coordonnées cartésiennes peuvent être trouvées en utilisant les conversions suivantes.
La troisième équation est juste une reconnaissance que la coordonnée \(z\) d’un point en coordonnées cartésiennes et polaires est la même.
De même, si nous avons un point en coordonnées cartésiennes, les coordonnées cylindriques peuvent être trouvées en utilisant les conversions suivantes.
Regardons rapidement quelques surfaces en coordonnées cylindriques.
- \(r = 5\)
- \({r^2} + {z^2} = 100\)
- \(z = r\)
Afficher toutes les solutions Cacher toutes les solutions
En deux dimensions, nous savons que c’est un cercle de rayon 5. Puisque nous sommes maintenant en trois dimensions et qu’il n’y a pas de \(z\) dans l’équation, cela signifie qu’il est autorisé à varier librement. Ainsi, pour toute \(z\) donnée, nous aurons un cercle de rayon 5 centré sur l’axe \(z\).
En d’autres termes, nous aurons un cylindre de rayon 5 centré sur l’axe \(z\).
b \({r^2} + {z^2} = 100\) Afficher la solution
Cette équation sera facile à identifier une fois que nous aurons reconverti en coordonnées cartésiennes.
Donc, il s’agit d’une sphère centrée à l’origine et de rayon 10.
c \(z = r\) Show Solution
Encore, celle-ci ne sera pas trop mal si on la reconvertit en coordonnées cartésiennes. Pour des raisons qui seront apparentes par la suite, nous allons d’abord élever les deux côtés au carré, puis convertir.
D’après la section sur les surfaces quadriques, nous savons que c’est l’équation d’un cône.
.