Dans une recherche qui étudie une relation potentielle de cause à effet, une variable confusionnelle est une troisième variable non mesurée qui influence à la fois la cause supposée et l’effet supposé.
Il est important d’envisager les variables confusionnelles potentielles et d’en tenir compte dans votre plan de recherche pour garantir la validité de vos résultats.
Qu’est-ce qu’une variable confusionnelle ?
Les variables confusionnelles, également appelées facteurs de confusion ou facteurs confondants, sont étroitement liées aux variables indépendantes et dépendantes d’une étude. Une variable doit remplir deux conditions pour être un facteur de confusion :
- Elle doit être corrélée avec la variable indépendante. Il peut s’agir d’une relation causale, mais ce n’est pas obligatoire.
- Elle doit avoir un lien de causalité avec la variable dépendante.
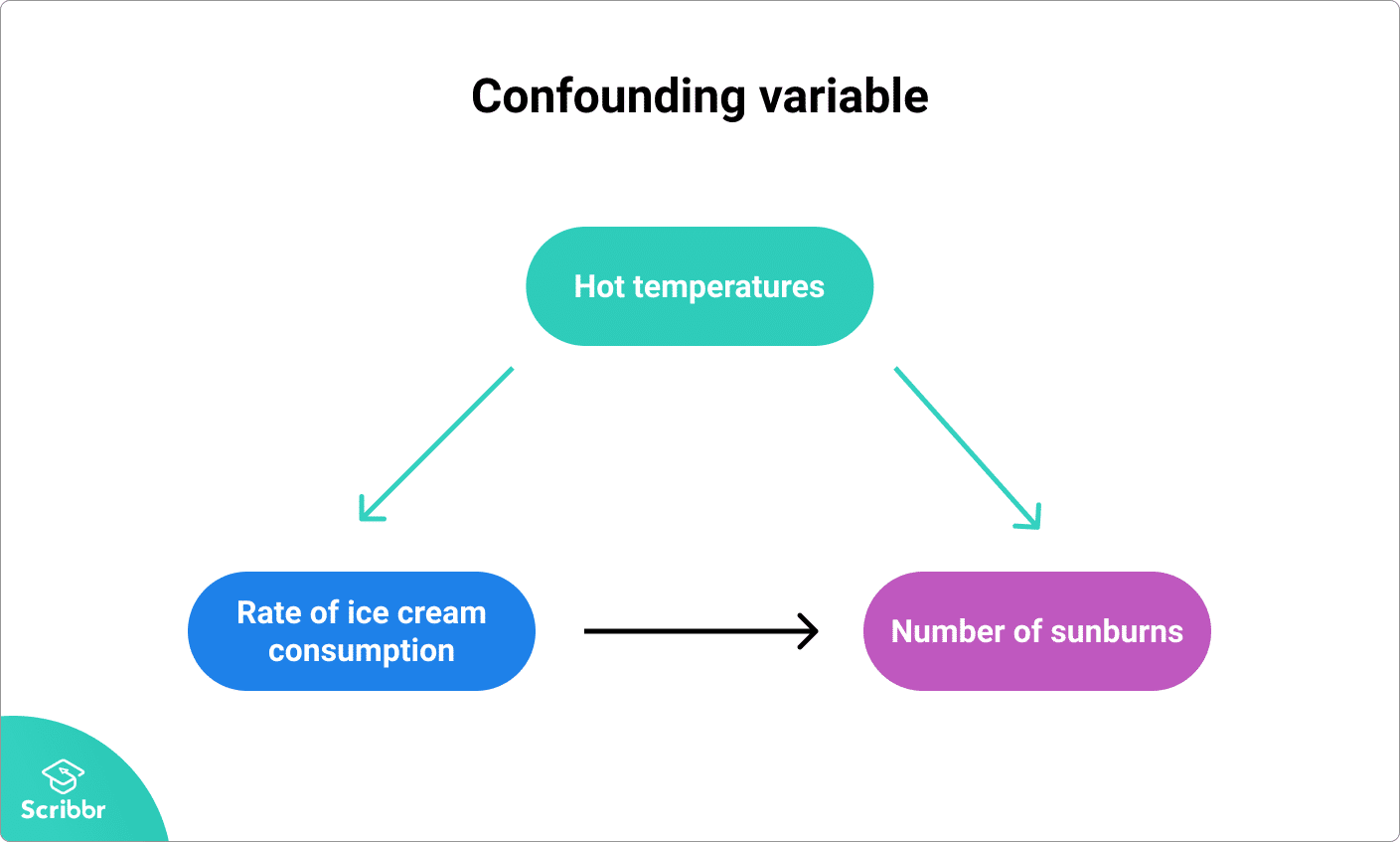
Ici, la variable confusionnelle est la température : les températures chaudes incitent les gens à la fois à manger plus de crème glacée et à passer plus de temps à l’extérieur sous le soleil, ce qui entraîne davantage de coups de soleil.

Pourquoi les variables confusionnelles sont importantes
Pour garantir la validité interne de votre recherche, vous devez tenir compte des variables confusionnelles. Si vous ne le faites pas, vos résultats peuvent ne pas refléter la relation réelle entre les variables qui vous intéressent.
Par exemple, vous pouvez trouver une relation de cause à effet qui n’existe pas réellement, car l’effet que vous mesurez est causé par la variable de confusion (et non par votre variable indépendante).
Pas nécessairement. Peut-être que les États où le marché de l’emploi est meilleur sont plus susceptibles d’augmenter leur salaire minimum, plutôt que l’inverse. Vous devez tenir compte des tendances antérieures de l’emploi dans votre analyse de l’impact du salaire minimum sur l’emploi, ou vous pourriez trouver une relation de cause à effet là où il n’y en a pas.
Même si vous identifiez correctement une relation de cause à effet, les variables confusionnelles peuvent entraîner une sur- ou une sous-estimation de l’impact de votre variable indépendante sur votre variable dépendante.
Comment réduire l’impact des variables confondantes
Il existe plusieurs méthodes pour tenir compte des variables confondantes. Vous pouvez utiliser les méthodes suivantes lorsque vous étudiez n’importe quel type de sujets – humains, animaux, plantes, produits chimiques, etc. Chaque méthode a ses propres avantages et inconvénients.
Restriction
Dans cette méthode, vous restreignez votre groupe de traitement en n’incluant que les sujets ayant les mêmes valeurs de facteurs de confusion potentiels.
Comme ces valeurs ne diffèrent pas entre les sujets de votre étude, elles ne peuvent pas être corrélées avec votre variable indépendante et ne peuvent donc pas confondre la relation de cause à effet que vous étudiez.
- Relativement facile à mettre en œuvre
- Restreint beaucoup votre échantillon
- Vous risquez de ne pas prendre en compte d’autres facteurs de confusion potentiels
Matching
Dans cette méthode, vous sélectionnez un groupe de comparaison qui correspond au groupe de traitement. Chaque membre du groupe de comparaison doit avoir un homologue dans le groupe de traitement avec les mêmes valeurs de facteurs de confusion potentiels, mais des valeurs de variables indépendantes différentes.
Cela vous permet d’éliminer la possibilité que des différences dans les variables de confusion causent la variation des résultats entre le groupe de traitement et le groupe de comparaison. Si vous avez pris en compte tous les facteurs de confusion potentiels, vous pouvez donc conclure que la différence dans la variable indépendante doit être la cause de la variation de la variable dépendante.
Chaque sujet suivant un régime pauvre en glucides est apparié avec un autre sujet présentant les mêmes caractéristiques mais ne suivant pas le régime. Ainsi, pour chaque homme de 40 ans très instruit qui suit un régime pauvre en glucides, vous trouvez un autre homme de 40 ans très instruit qui ne le fait pas, afin de comparer la perte de poids entre les deux sujets. Vous faites de même pour tous les autres sujets de votre échantillon de traitement.
- Vous permet d’inclure plus de sujets que la restriction
- Peut s’avérer difficile à mettre en œuvre car vous avez besoin de paires de sujets qui correspondent sur chaque variable de confusion potentielle
- Les autres variables sur lesquelles vous ne pouvez pas correspondre pourraient également être des variables de confusion
Contrôle statistique
Si vous avez déjà collecté les données, vous pouvez inclure les éventuels facteurs de confusion comme variables de contrôle dans vos modèles de régression ; de cette manière, vous contrôlerez l’impact de la variable de confusion.
Tout effet que la variable confusionnelle potentielle a sur la variable dépendante apparaîtra dans les résultats de la régression et vous permettra de séparer l’impact de la variable indépendante.
- Facile à mettre en œuvre
- Peut être effectué après la collecte des données
- Vous ne pouvez contrôler que les variables que vous observez directement, mais d’autres variables de confusion que vous n’avez pas prises en compte pourraient subsister
Randomisation
Une autre façon de minimiser l’impact des variables de confusion est de randomiser les valeurs de votre variable indépendante. Par exemple, si certains de vos participants sont assignés à un groupe de traitement tandis que d’autres sont dans un groupe de contrôle, vous pouvez assigner au hasard des participants à chaque groupe.
La randomisation garantit qu’avec un échantillon suffisamment grand, toutes les variables confusionnelles potentielles – même celles que vous ne pouvez pas observer directement dans votre étude – auront la même valeur moyenne entre les différents groupes. Comme ces variables ne diffèrent pas selon l’affectation des groupes, elles ne peuvent pas être corrélées à votre variable indépendante et ne peuvent donc pas confondre votre étude.
Comme cette méthode vous permet de tenir compte de toutes les variables confusionnelles potentielles, ce qui est presque impossible à faire autrement, elle est souvent considérée comme le meilleur moyen de réduire l’impact des variables confusionnelles.
- Vous permet de tenir compte de toutes les variables confusionnelles possibles, y compris celles que vous n’observez peut-être pas directement
- Considérée comme la meilleure méthode pour minimiser l’impact des variables confusionnelles
- La plus difficile à réaliser
- Doit être mise en œuvre avant de commencer la collecte des données. collecte des données
- Vous devez vous assurer que seules les personnes du groupe de traitement (et non de contrôle) reçoivent le traitement
Questions fréquemment posées sur les variables de confusion
Une variable confondante, également appelée facteur de confusion ou facteur de confusion, est une troisième variable dans une étude examinant une relation de cause à effet potentielle.
Une variable confondante est liée à la fois à la cause supposée et à l’effet supposé de l’étude. Il peut être difficile de séparer le véritable effet de la variable indépendante de l’effet de la variable confusionnelle.
Dans votre plan de recherche, il est important d’identifier les variables confusionnelles potentielles et de planifier la façon dont vous réduirez leur impact.
Une variable confondante est étroitement liée aux variables indépendantes et dépendantes d’une étude. Une variable indépendante représente la cause supposée, tandis que la variable dépendante est l’effet supposé. Une variable confondante est une troisième variable qui influence à la fois les variables indépendantes et dépendantes.
Ne pas tenir compte des variables confondantes peut vous amener à estimer de manière erronée la relation entre vos variables indépendantes et dépendantes.
Pour assurer la validité interne de votre recherche, vous devez tenir compte de l’impact des variables confusionnelles. Si vous ne les prenez pas en compte, vous risquez de surestimer ou de sous-estimer la relation causale entre vos variables indépendantes et dépendantes, ou même de trouver une relation causale là où il n’y en a pas.
Il existe plusieurs méthodes que vous pouvez utiliser pour diminuer l’impact des variables confusionnelles sur votre recherche : la restriction, l’appariement, le contrôle statistique et la randomisation.
Dans le cadre de la restriction, vous limitez votre échantillon en n’incluant que certains sujets qui ont les mêmes valeurs de variables confusionnelles potentielles.
Dans le cadre de l’appariement, vous faites correspondre chacun des sujets de votre groupe de traitement avec un homologue du groupe de comparaison. Les sujets appariés ont les mêmes valeurs sur toutes les variables de confusion potentielles, et ne diffèrent que par la variable indépendante.
Dans le contrôle statistique, vous incluez les facteurs de confusion potentiels en tant que variables dans votre régression.
Dans la randomisation, vous attribuez au hasard le traitement (ou la variable indépendante) de votre étude à un nombre suffisamment important de sujets, ce qui vous permet de contrôler toutes les variables de confusion potentielles.
.
