« Degré » peut signifier plusieurs choses en mathématiques :
- En géométrie, un degré (°) est une façon de mesurer les angles,
- Mais ici nous regardons ce que le degré signifie en algèbre.
En algèbre, « degré » est parfois appelé « ordre »
Degré d’un polynôme (à une variable)
Un polynôme ressemble à ceci :
exemple de polynôme
celui-ci a 3 termes
Le Degré (pour un polynôme à une variable, comme x) est :
le plus grand exposant de cette variable.
Plus d’exemples :
| 4x | Le degré est 1 (une variable sans exposant a en fait un exposant de 1) |
|
| 4×3 – x + 3 | Le Degré est 3 (plus grand exposant de x) | . |
| x2 + 2×5 – x | Le degré est 5 (plus grand exposant de x) | |
| z2 – z + 3 | Le degré est 2 (plus grand exposant de z) |
Noms des degrés
Quand on connaît le degré, on peut aussi lui donner un nom !
| Degree | Name | Exemple |
|---|---|---|
| 0 | Constant | 7 | 1 | Linéaire | x+3 |
| 2 | Quadratic | x2-x+2 |
| 3 | Cubique | x3-x2+5 |
| 4 | Quartic | 6×4-x3+x-2 |
| 5 | Quintique | x5-3×3+x2+8 |
Exemple : y = 2x + 7 a un degré de 1, c’est donc une équation linéaire
Exemple : 5w2 – 3 a un degré de 2, elle est donc quadratique
Les équations d’ordre supérieur sont généralement plus difficiles à résoudre :
- Les équations linéaires sont faciles à résoudre
- Les équations quadratiques sont un peu plus difficiles à résoudre
- Les équations cubiques sont encore plus difficiles, mais il existe des formules pour aider
- Les équations quariques peuvent aussi être résolues, mais les formules sont très compliquées
- Les équations quintiques n’ont pas de formules, et peuvent parfois être insolubles !
Degree of a Polynomial with More Than One Variable
Lorsqu’un polynôme a plus d’une variable, nous devons regarder chaque terme. Les termes sont séparés par des signes + ou – :
exemple de polynôme
avec plus d’une variable
Pour chaque terme :
- Trouver le degré en additionnant les exposants de chaque variable qui le compose,
Le plus grand de ces degrés est le degré du polynôme.
Exemple : quel est le degré de ce polynôme :
Vérification de chaque terme :
- 5xy2 a un degré de 3 (x a un exposant de 1, y en a 2, et 1+2=3)
- 3x a un degré de 1 (x a un exposant de 1)
- 5y3 a un degré de 3 (y a un exposant de 3)
- 3 a un degré de 0 (pas de variable)
Le plus grand degré de ceux-là est 3 (en fait deux termes ont un degré de 3), donc le polynôme a un degré de 3
Exemple : quel est le degré de ce polynôme :
4z3 + 5y2z2 + 2yz
Vérification de chaque terme :
- 4z3 a un degré de 3 (z a un exposant de 3)
- 5y2z2 a un degré de 4 (y a un exposant de 2, z a 2, et 2+2=4)
- 2yz a un degré de 2 (y a un exposant de 1, z a 1, et 1+1=2)
Le plus grand degré de ceux-ci est 4, donc le polynôme a un degré de 4
Ecriture
Au lieu de dire « le degré de (quoi que ce soit) est 3 », nous l’écrivons comme ceci :
Lorsque l’expression est une fraction
Nous pouvons calculer le degré d’une expression rationnelle (celle qui se présente sous la forme d’une fraction) en prenant le degré du haut (numérateur) et en soustrayant le degré du bas (dénominateur).
Voici trois exemples :
Calculer d’autres types d’expressions
Avertissement : Des idées avancées en perspective !
On peut parfois calculer le degré d’une expression en divisant …
- le logarithme de la fonction par
- le logarithme de la variable
… puis faire cela pour des valeurs de plus en plus grandes, pour voir où la réponse « se dirige ».
(Plus correctement, nous devrions travailler sur la limite à l’infini de ln(f(x))/ln(x), mais je veux juste garder cela simple ici).
|
Note : « ln » est la fonction logarithme naturel. |
 |
Voici un exemple :
Exemple : Quel est le degré de (3 plus la racine carrée de x) ?
Essayons des valeurs croissantes de x :
| x | ln( ) |
ln(x) | ln() / ln(x) |
|---|---|---|---|
| 2 | 1.48483 | 0.69315 | 2,1422 |
| 4 | 1.60944 | 1,38629 | 1.1610 | 10 | 1,81845 | 2.30259 | 0,7897 |
| 100 | 2.56495 | 4,60517 | 0.5570 | 1 000 | 3,54451 | 6.90776 | 0,5131 |
| 10 000 | 4.63473 | 9,21034 | 0.5032 | 100 000 | 5,76590 | 11.51293 | 0,5008 |
| 1 000 000 | 6.91075 | 13,81551 | 0.5002 |
Regardons le tableau :
- lorsque x devient plus grand alors ln(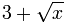). / ln(x) se rapproche de plus en plus de 0,5
Donc le degré est de 0.5 (en d’autres termes 1/2)
(Note : cela s’accorde bien avec x½ = racine carrée de x, voir Exposants fractionnaires)
Quelques valeurs de degrés
| Expression | Degré |
|---|---|
| log(x) | 0 |
| ex | ∞ |
| 1/x | -1 |
 |
1/2 |
.