- Comportement de la moyenne de l’échantillon (x-bar)
- La distribution d’échantillonnage de la moyenne de l’échantillon
Comportement de la moyenne de l’échantillon (x-bar)
Jusqu’ici, nous avons discuté du comportement de la statistique p-hat, la proportion de l’échantillon, par rapport au paramètre p, la proportion de la population (lorsque la variable d’intérêt est catégorique).
Nous allons maintenant explorer le comportement de la statistique x-bar, la moyenne de l’échantillon, par rapport au paramètre μ (mu), la moyenne de la population (lorsque la variable d’intérêt est quantitative).
Débutons par un exemple.
EXEMPLE 9 : Comportement des moyennes d’un échantillon
On enregistre les poids de naissance de tous les bébés d’une ville. Le poids moyen à la naissance est de 3 500 grammes, µ = mu = 3 500 g. Si nous collectons de nombreux échantillons aléatoires de 9 bébés à la fois, comment pensez-vous que les moyennes des échantillons vont se comporter ?
Ici encore, nous travaillons avec une variable aléatoire, puisque les échantillons aléatoires auront des moyennes qui varient de manière imprévisible à court terme mais présentent des tendances à long terme.
Sur la base de notre intuition et de ce que nous avons appris sur le comportement des proportions d’échantillons, nous pourrions nous attendre à ce qui suit concernant la distribution des moyennes d’échantillons :
Centre : Certaines moyennes d’échantillons se situeront dans la partie basse – disons 3 000 grammes ou plus – tandis que d’autres se situeront dans la partie haute – disons 4 000 grammes ou plus. Dans le cas d’un échantillonnage répété, nous pourrions nous attendre à ce que les échantillons aléatoires se rapprochent en moyenne de la moyenne sous-jacente de la population, soit 3 500 g. En d’autres termes, la moyenne des moyennes d’échantillons sera µ (mu), tout comme la moyenne des proportions d’échantillons était p.
Etendue : Pour les grands échantillons, nous pourrions nous attendre à ce que les moyennes des échantillons ne s’éloignent pas trop de la moyenne de la population de 3 500. Des moyennes d’échantillon inférieures à 3 000 ou supérieures à 4 000 pourraient être surprenantes. Pour les échantillons plus petits, nous serions moins surpris par des moyennes d’échantillons qui s’écartent beaucoup de 3 500. En d’autres termes, on peut s’attendre à une plus grande variabilité des moyennes d’échantillons pour les petits échantillons. Ainsi, la taille de l’échantillon jouera à nouveau un rôle dans la dispersion de la distribution des mesures de l’échantillon, comme nous l’avons observé pour les proportions de l’échantillon.
La forme : Les moyennes d’échantillon les plus proches de 3 500 seront les plus courantes, les moyennes d’échantillon éloignées de 3 500 dans chaque direction étant progressivement moins probables. En d’autres termes, la forme de la distribution des moyennes d’échantillons devrait se gonfler au milieu et s’effiler aux extrémités avec une forme qui est en quelque sorte normale. C’est, encore une fois, ce que nous avons vu lorsque nous avons examiné les proportions de l’échantillon.
Commentaire:
- La distribution des valeurs de la moyenne de l’échantillon (x-bar) dans des échantillons répétés est appelée la distribution d’échantillonnage de x-bar.
Regardons une simulation:
Les résultats que nous avons trouvés dans nos simulations ne sont pas surprenants. La théorie avancée des probabilités le confirme en affirmant ce qui suit :
La distribution d’échantillonnage de la moyenne de l’échantillon
Si des échantillons aléatoires répétés d’une taille n donnée sont prélevés dans une population de valeurs pour une variable quantitative, où la moyenne de la population est μ (mu) et l’écart-type de la population est σ (sigma), alors la moyenne de toutes les moyennes des échantillons (x-bars) est la moyenne de la population μ (mu).
Pour ce qui est de la dispersion de toutes les moyennes d’échantillons, la théorie dicte le comportement de manière beaucoup plus précise que de dire qu’il y a moins de dispersion pour les plus grands échantillons. En fait, l’écart-type de toutes les moyennes d’échantillons est directement lié à la taille de l’échantillon, n, comme indiqué ci-dessous.
![]()
Puisque la racine carrée de la taille de l’échantillon n apparaît au dénominateur, l’écart-type diminue effectivement lorsque la taille de l’échantillon augmente.
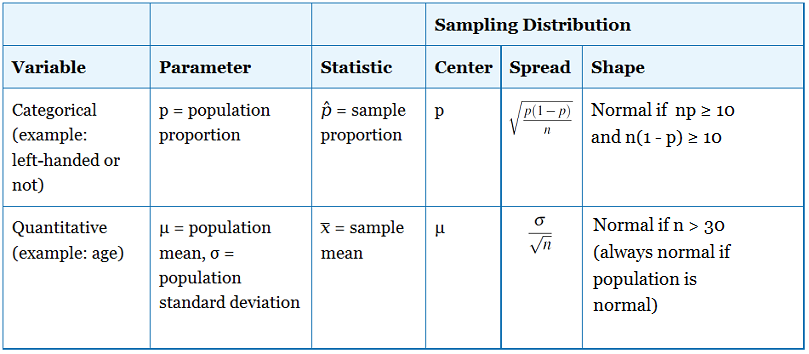
Considérons ce que nous savons maintenant sur les distributions d’échantillonnage des moyennes et des proportions d’échantillon.

Nous allons maintenant étudier la forme de la distribution d’échantillonnage des moyennes d’échantillon. Lorsque nous discutions de la distribution d’échantillonnage des proportions de l’échantillon, nous avons dit que cette distribution est approximativement normale si np ≥ 10 et n(1 – p) ≥ 10. En d’autres termes, nous avions une ligne directrice basée sur la taille de l’échantillon pour déterminer les conditions dans lesquelles nous pouvions utiliser les calculs de probabilité normale pour les proportions de l’échantillon.
Quand la distribution des moyennes de l’échantillon sera-t-elle approximativement normale ? Cela dépend-il de la taille de l’échantillon ?
Il semble raisonnable qu’une population avec une distribution normale aura des moyennes d’échantillon qui sont normalement distribuées même pour de très petits échantillons. Nous avons vu cela illustré dans la simulation précédente avec des échantillons de taille 10.
Que se passe-t-il si la distribution de la variable dans la population est fortement asymétrique ? Les moyennes des échantillons ont-elles aussi une distribution asymétrique ? Si nous prenons de très grands échantillons, les moyennes d’échantillon deviendront-elles plus normalement distribuées ?
Dans la prochaine simulation, nous étudierons ces questions.
Pour résumer, la distribution des moyennes d’un échantillon sera approximativement normale tant que la taille de l’échantillon est suffisamment grande. Cette découverte est probablement le résultat le plus important présenté dans les cours d’introduction aux statistiques. Elle est énoncée formellement sous le nom de Théorème de la limite centrale.
Nous dépendrons encore et encore du Théorème de la limite centrale pour effectuer des calculs de probabilité normale lorsque nous utiliserons les moyennes d’échantillons pour tirer des conclusions sur une moyenne de population. Nous savons maintenant que nous pouvons le faire même si la distribution de la population n’est pas normale.
De quelle taille d’échantillon avons-nous besoin pour supposer que les moyennes d’échantillon seront normalement distribuées ? Eh bien, cela dépend vraiment de la distribution de la population, comme nous l’avons vu dans la simulation. La règle générale est que les échantillons de taille 30 ou plus auront une distribution assez normale, quelle que soit la forme de la distribution de la variable dans la population.
Commentaire:
- Pour les variables catégorielles, notre affirmation selon laquelle les proportions d’échantillon sont approximativement normales pour un nombre n suffisamment grand est en fait un cas particulier du théorème de la limite centrale. Dans ce cas, nous considérons les données comme des 0 et des 1 et la » moyenne » de ces 0 et de ces 1 est égale à la proportion dont nous avons parlé.
Avant de travailler sur quelques exemples, comparons ce que nous savons maintenant sur les distributions d’échantillonnage des moyennes et des proportions d’échantillon.
EXEMPLE 10 : Utilisation de la distribution d’échantillonnage de x-bar
La taille des ménages aux États-Unis a une moyenne de 2,6 personnes et un écart-type de 1,4 personne. Il devrait être clair que cette distribution est asymétrique à droite car la plus petite valeur possible est un ménage de 1 personne mais les plus grands ménages peuvent être très grands en effet.
(a) Quelle est la probabilité qu’un ménage choisi au hasard ait plus de 3 personnes?
Une approximation normale ne devrait pas être utilisée ici, car la distribution des tailles des ménages serait considérablement asymétrique à droite. Nous ne disposons pas de suffisamment d’informations pour résoudre ce problème.
(b) Quelle est la probabilité que la taille moyenne d’un échantillon aléatoire de 10 ménages soit supérieure à 3 ?
Selon n’importe qui, 10 est un échantillon de petite taille. Le théorème de la limite centrale ne garantit pas que la moyenne d’un échantillon provenant d’une population asymétrique soit approximativement normale, à moins que la taille de l’échantillon soit grande.
(c) Quelle est la probabilité que la taille moyenne d’un échantillon aléatoire de 100 ménages soit supérieure à 3 ?
Nous pouvons maintenant invoquer le théorème de la limite centrale : même si la distribution de la taille des ménages X est asymétrique, la distribution de la taille moyenne des ménages de l’échantillon (x-bar) est approximativement normale pour un grand échantillon tel que 100. Sa moyenne est la même que la moyenne de la population, 2.6, et son écart-type est l’écart-type de la population divisé par la racine carrée de la taille de l’échantillon :

To find
![]()
nous normalisons 3 à en un z-score en soustrayant la moyenne et en divisant le résultat par l’écart-type (de la moyenne de l’échantillon). Nous pouvons ensuite trouver la probabilité à l’aide de la calculatrice ou du tableau normal standard.

Les ménages de plus de 3 personnes sont, bien sûr, assez courants, mais il serait extrêmement inhabituel que la taille moyenne d’un échantillon de 100 ménages soit supérieure à 3.
Le but de l’activité suivante est de donner une pratique guidée pour trouver la distribution d’échantillonnage de la moyenne de l’échantillon (x-bar), et de l’utiliser pour en savoir plus sur la probabilité d’obtenir certaines valeurs de x-bar.