Objetivos de aprendizaje
Al finalizar esta sección, serás capaz de:
- Explicar cómo los intervalos de tiempo pueden medirse de forma diferente en distintos marcos de referencia.
- Describir cómo distinguir un intervalo de tiempo propio de uno dilatado.
- Describir el significado del experimento de los muones.
- Explicar por qué la paradoja de los gemelos no es una contradicción.
- Calcular la dilatación del tiempo dada la velocidad de un objeto en un marco determinado.
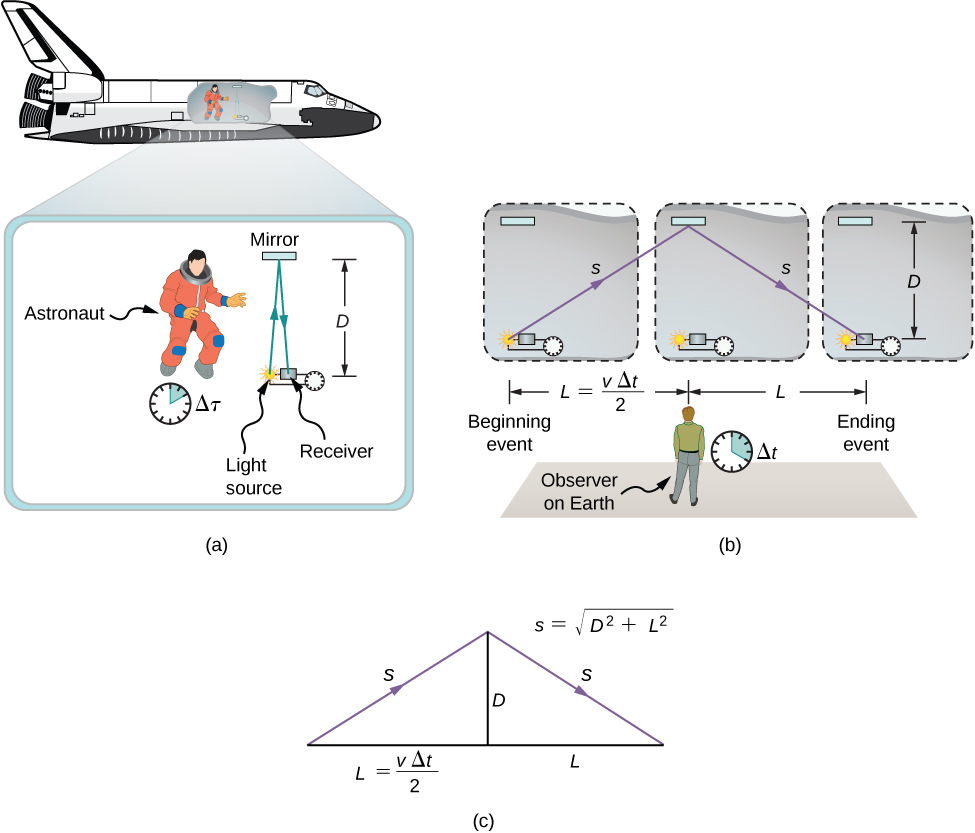
El análisis de la simultaneidad muestra que los postulados de Einstein implican un efecto importante: Los intervalos de tiempo tienen valores diferentes cuando se miden en diferentes marcos inerciales. Supongamos, por ejemplo, que un astronauta mide el tiempo que tarda un pulso de luz en recorrer una distancia perpendicular a la dirección del movimiento de su nave (en relación con un observador terrestre), rebotar en un espejo y regresar (Figura \(\PageIndex{1a})). ¿Cómo se compara el tiempo transcurrido que el astronauta mide en la nave espacial con el tiempo transcurrido que un observador terrestre mide al observar lo que ocurre en la nave espacial?
El examen de esta cuestión conduce a un resultado profundo. El tiempo transcurrido de un proceso depende del observador que lo mide. En este caso, el tiempo medido por el astronauta (dentro de la nave espacial, donde el astronauta está en reposo) es menor que el tiempo medido por el observador terrestre (hacia el que se mueve el astronauta). El tiempo transcurrido para el mismo proceso es diferente para los observadores, ya que la distancia que recorre el pulso de luz en el marco del astronauta es menor que en el marco terrestre, como se ve en la Figura \(\PageIndex{1b}\). La luz viaja a la misma velocidad en cada marco, por lo que tarda más tiempo en recorrer la mayor distancia en el marco terrestre.
Definición: Dilatación del tiempo
La dilatación del tiempo es el alargamiento del intervalo de tiempo entre dos sucesos para un observador en un marco inercial que se mueve respecto al marco de reposo de los sucesos (en el que los sucesos ocurren en el mismo lugar).
Para comparar cuantitativamente las mediciones de tiempo en los dos marcos inerciales, podemos relacionar las distancias en la Figura \(\PageIndex{1b}) entre sí, y luego expresar cada distancia en términos del tiempo de viaje (respectivamente \(\Delta t\) o \(\Delta \tau\)) del impulso en el marco de referencia correspondiente. La ecuación resultante puede entonces resolverse para \(\Delta t\) en términos de \(\Delta \tau\).
Las longitudes \(D\) y \(L\) en la figura \(\PageIndex{1c}) son los lados de un triángulo rectángulo con hipotenusa \(s\). A partir del teorema de Pitágoras,
Las longitudes \(2s\) y \(2L\) son, respectivamente, las distancias que el pulso de luz y la nave espacial recorren en el tiempo \(\Delta t\) en el marco del observador terrestre. La longitud \(D\) es la distancia que el pulso de luz recorre en el tiempo \(\Delta \tau\) en el marco del astronauta. Esto nos da tres ecuaciones:
2L &= v\Delta t; \ 2D &= c\Delta \tau. \end{align*}]
Nota que hemos utilizado el segundo postulado de Einstein tomando la velocidad de la luz como c en ambos marcos inerciales. Sustituimos estos resultados en la expresión anterior del teorema de Pitágoras:
Izquierda(c\dfrac{\Delta t}{2}\️)^2 &= \left(c\dfrac{\Delta \tau}{2}\️)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*}]
Entonces reordenamos para obtener
\N-
Finalmente, resolviendo para \(\Delta t\) en términos de \(\Delta \tau\) nos da
Esto es equivalente a
donde \(\gamma\) es el factor relativista (a menudo llamado factor de Lorentz) dado por
y \(v\) y \(c\) son las velocidades del observador en movimiento y de la luz, respectivamente.
Nótese la asimetría entre las dos medidas. Sólo una de ellas es una medida del intervalo de tiempo entre dos eventos -la emisión y la llegada del pulso de luz- en la misma posición. Es una medida del intervalo de tiempo en el marco de reposo de un solo reloj. La medición en el marco terrestre implica la comparación del intervalo de tiempo entre dos eventos que ocurren en lugares diferentes. El intervalo de tiempo entre eventos que ocurren en una sola ubicación tiene un nombre separado para distinguirlo del tiempo medido por el observador terrestre, y utilizamos el símbolo separado \(\Delta \tau\) para referirnos a él a lo largo de este capítulo.
Definición: Tiempo propio
El intervalo de tiempo propio \(\Delta \tau\) entre dos eventos es el intervalo de tiempo medido por un observador para el que ambos eventos ocurren en el mismo lugar.
La ecuación que relaciona \(\delta t\) y \(\Delta \tau) es realmente notable. En primer lugar, como ya se ha dicho, el tiempo transcurrido no es el mismo para diferentes observadores que se mueven uno respecto al otro, aunque ambos estén en marcos inerciales. Un intervalo de tiempo propio \(\Delta \tau\) para un observador que, como el astronauta, se mueve con el aparato, es menor que el intervalo de tiempo para otros observadores. Es el menor tiempo medido posible entre dos acontecimientos. El observador que se encuentra en tierra ve los intervalos de tiempo dentro del sistema en movimiento como dilatados (es decir, alargados) en relación a cómo los ve el observador que se mueve en relación a la Tierra dentro del sistema en movimiento. Por otra parte, según el observador que se encuentra en tierra, transcurre menos tiempo entre los eventos dentro del marco en movimiento. Obsérvese que el menor tiempo transcurrido entre los sucesos se da en el marco inercial en el que el observador ve que los sucesos (por ejemplo, la emisión y la llegada de la señal luminosa) ocurren en el mismo punto.
Este efecto del tiempo es real y no está causado por relojes inexactos o mediciones inadecuadas. Las mediciones del intervalo de tiempo del mismo evento difieren para los observadores en movimiento relativo. La dilatación del tiempo es una propiedad intrínseca del propio tiempo. Se observa que todos los relojes que se mueven con respecto a un observador, incluidos los relojes biológicos, como los latidos del corazón de una persona, o el envejecimiento, funcionan más lentamente en comparación con un reloj que está inmóvil con respecto al observador.
Nótese que si la velocidad relativa es mucho menor que la velocidad de la luz (v << c), entonces \(v^2/c^2\) es extremadamente pequeño, y los tiempos transcurridos \(\Delta t\) y \(\Delta \tau\) son casi iguales. A bajas velocidades, la física basada en la relatividad moderna se aproxima a la física clásica: las experiencias cotidianas implican efectos relativistas muy pequeños. Sin embargo, para velocidades cercanas a la de la luz, \(v^2/c^2\) es cercana a uno, por lo que \(\sqrt{1 – v^2/c^2}\ es muy pequeña y \(\Delta t\) se vuelve significativamente mayor que \(\Delta \tau\).
Vida media de un muón
Existe una considerable evidencia experimental de que la ecuación \(\Delta t = \gamma \Delta \tau\) es correcta. Un ejemplo lo encontramos en las partículas de rayos cósmicos que llueven continuamente sobre la Tierra desde el espacio profundo. Algunas colisiones de estas partículas con núcleos de la atmósfera superior dan lugar a partículas de corta duración llamadas muones. La vida media (cantidad de tiempo para que la mitad de un material decaiga) de un muón es de 1,52 μs cuando está en reposo respecto al observador que mide la vida media. Este es el intervalo de tiempo adecuado \(\Delta \tau\). Este corto tiempo permite que muy pocos muones alcancen la superficie de la Tierra y sean detectados si las suposiciones newtonianas sobre el tiempo y el espacio fueran correctas. Sin embargo, los muones producidos por las partículas de los rayos cósmicos tienen un rango de velocidades, y algunos se mueven cerca de la velocidad de la luz. Se ha descubierto que la vida media del muón medida por un observador terrestre (\(\Delta t\)) varía con la velocidad exactamente como predice la ecuación \(\Delta t = \gamma \Delta \tau). Cuanto más rápido se mueve el muón, más tiempo vive. En la Tierra vemos que el muón dura mucho más de lo que predice su vida media dentro de su propio marco de reposo. Visto desde nuestro marco, el muón decae más lentamente que cuando está en reposo respecto a nosotros. Como resultado, una fracción mucho mayor de muones llega al suelo.
Antes de presentar el primer ejemplo de resolución de un problema de relatividad, exponemos una estrategia que puedes utilizar como guía para estos cálculos.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: RELATIVIDAD
- Haz una lista de lo que se da o puede inferirse del problema tal y como está planteado (identifica los conocidos). Busque, en particular, información sobre la velocidad relativa v.
- Identifique exactamente lo que hay que determinar en el problema (identifique las incógnitas).
- Asegúrese de que entiende los aspectos conceptuales del problema antes de hacer cualquier cálculo (exprese la respuesta como una ecuación). Decide, por ejemplo, qué observador ve el tiempo dilatado o la longitud contraída antes de trabajar con las ecuaciones o utilizarlas para realizar el cálculo. Si ha pensado en quién ve qué, quién se mueve con el suceso observado, quién ve el tiempo propio, etc., le resultará mucho más fácil determinar si su cálculo es razonable.
- Determine el tipo de cálculo principal que debe realizar para hallar las incógnitas identificadas anteriormente (haga el cálculo). Encontrará el resumen de la sección útil para determinar si se trata de una contracción de longitud, energía cinética relativista o algún otro concepto.
Note que no debe redondear durante el cálculo. Como se indica en el texto, a menudo debe realizar sus cálculos con muchos dígitos para ver el efecto deseado. Puede redondear al final de la solución del problema, pero no utilice un número redondeado en un cálculo posterior. Además, comprueba la respuesta para ver si es razonable: ¿Tiene sentido? Esto puede ser más difícil en el caso de la relatividad, que tiene pocos ejemplos cotidianos que proporcionen experiencia sobre lo que es razonable. Pero puedes buscar velocidades mayores que c o efectos relativistas que estén en la dirección equivocada (como una contracción del tiempo donde se esperaba una dilatación).
Ejemplo \N(\PageIndex{1A}\N): Dilatación del tiempo en un vehículo de alta velocidad
El Vehículo Tecnológico Hipersónico 2 (HTV-2) es un vehículo cohete experimental capaz de viajar a 21.000 km/h (5830 m/s). Si un reloj electrónico en el HTV-2 mide un intervalo de tiempo de exactamente 1-s de duración, ¿cuál sería el intervalo de tiempo que medirían los observadores en la Tierra?
Estrategia
Aplique la fórmula de dilatación del tiempo para relacionar el intervalo de tiempo propio de la señal en el HTV-2 con el intervalo de tiempo medido en tierra.
Solución
- Identifique los conocidos: \(\Delta \tau = 1 \, s\); \(v = 5830m/s.\N-)
- Identificar la incógnita: \(\Delta t\).
- Expresa la respuesta como una ecuación:
- Haga el cálculo. Utiliza la expresión de \(\gamma\) para determinar \(\Delta t\) a partir de \(\Delta \tau):
\N- &= 1.000000000189 \N-, s \N- &= 1 \N-, s + 1.89 \N- 10^{-10}s. \end{align*}]
Significado
La altísima velocidad del HTV-2 sigue siendo sólo 10-5 veces la velocidad de la luz. Los efectos relativistas para el HTV-2 son despreciables a casi todos los efectos, pero no son nulos.
¿Qué velocidades son relativistas?
¿Cuál es la velocidad que debe alcanzar un vehículo para que 1 segundo de tiempo medido en el reloj de un pasajero en el vehículo difiera en un 1% para un observador que lo mida desde el suelo en el exterior?
Estrategia
Utiliza la fórmula de dilatación del tiempo para hallar v/c para la relación de tiempos dada.
Solución
- Identificar lo conocido:
\N
- Identificar la incógnita: v/c.
- Expresar la respuesta en forma de ecuación:
&= \dfrac{1}{sqrt{1} – v^2/c^2}\Delta \tau \dfrac{\Delta \tau}{Delta t} &= \sqrt{1 – v^2/c^2} \\N – Izquierda(\N – Delta \N – Delta t) ^2 &= 1 – \N – v^2}{c^2} \N – \N – dfrac{v}{c} &= \sqrt{1 – (\Delta \tau/\Delta t)^2}. \end{align*}]
- Haga el cálculo:
\N-
Significado
El resultado muestra que un objeto debe viajar a muy aproximadamente el 10% de la velocidad de la luz para que su movimiento produzca efectos significativos de dilatación temporal relativista.
Calcular \(\Delta t\) para un evento relativista
Supongamos que un rayo cósmico que colisiona con un núcleo en la atmósfera superior de la Tierra produce un muón que tiene una velocidad \(v = 0,950c\). El muón viaja entonces a velocidad constante y vive 2,20 μs medidos en el marco de referencia del muón. ¿Cuánto tiempo vive el muón medido por un observador terrestre (Figura \(\PageIndex{2}\))?
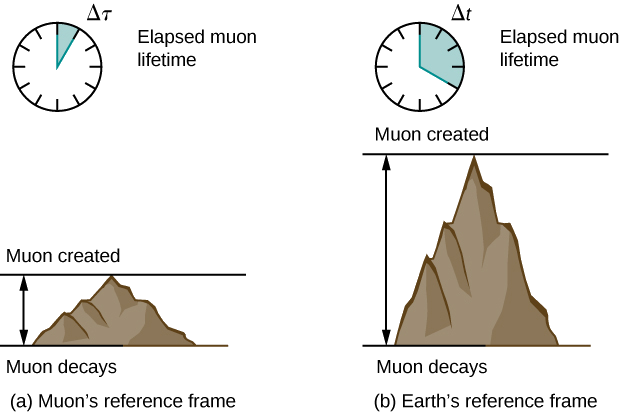
Como veremos más adelante, en el marco de referencia del muón, éste recorre una distancia menor que la medida en el marco de referencia terrestre.
Estrategia
Un reloj que se mueve con el muón mide el tiempo propio de su proceso de desintegración, por lo que el tiempo que nos dan es \(\Delta \tau = 2,20 \mu s\). El observador terrestre mide \(\Delta t\) según la ecuación \(\Delta t = \gamma \Delta \tau\). Como la velocidad está dada, podemos calcular el tiempo en el marco de referencia de la Tierra.
Solución
- Identificar las conocidas: \(v = 0,950c\); \(\delta \tau = 2,20 \mu s\).
- Identificar la incógnita: \(\Delta t\).
- Expresa la respuesta como una ecuación. Utiliza:
\
con
\Ncontra el cálculo. Utiliza la expresión de \(\gamma\) para determinar \(\Delta t\) a partir de \(\Delta \tau):
\N- &=dfrac{1}{{cuadrado{1} – \dfrac{v^2}{c^2}}{delta \tau \N- &=dfrac{2,20 \mu s}{cuadrado{1} – (0,950)^2} &= 7,05 \Nmu s.|end{align*}]
Recuerda mantener las cifras significativas adicionales hasta la respuesta final.
Significativo
Una implicación de este ejemplo es que debido a que \(\gamma = 3,20\) al 95,0% de la velocidad de la luz (\(v = 0,950c\)), los efectos relativistas son significativos. Los dos intervalos de tiempo difieren en un factor de 3,20, cuando clásicamente serían iguales. Algo que se mueve a 0,950c se dice que es altamente relativista.
Una pantalla de televisión no plana, de estilo antiguo (Figura \(\PageIndex{3}\)) funciona acelerando los electrones a una corta distancia hasta alcanzar una velocidad relativista, y luego utilizando campos electromagnéticos para controlar dónde incide el haz de electrones en una capa fluorescente en la parte delantera del tubo. Supongamos que los electrones viajan a \(6,00 \times 10^7 m/s\) a través de una distancia de 0,200m0,200m desde el inicio del haz hasta la pantalla.
- ¿Cuál es el tiempo de viaje de un electrón en el marco de reposo del televisor?
- ¿Cuál es el tiempo de viaje del electrón en su propio marco de reposo?
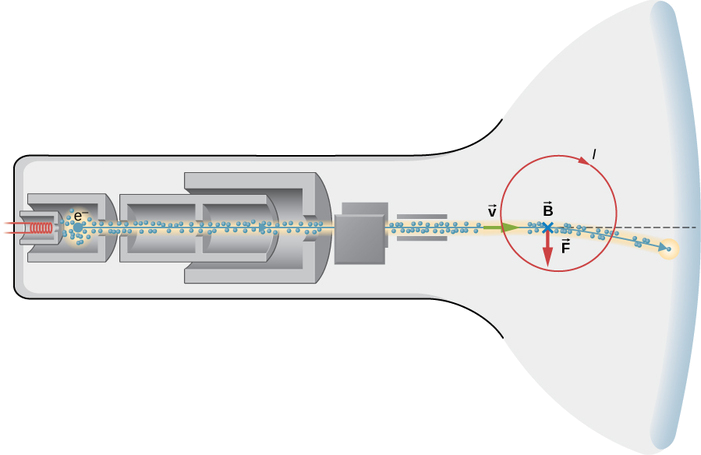
Estrategia para (a)
(a) Calcular el tiempo a partir de \N(vt = d\). Aunque la velocidad es relativista, el cálculo se realiza íntegramente en un marco de referencia, por lo que no interviene la relatividad.
Solución
- Identificar los conocidos:
\
- Identificar la incógnita: el tiempo de viaje \(\Delta t\).
- Expresar la respuesta en forma de ecuación:
\N
- Haz el cálculo:
&= 3,33 \times 10^{-9} \N -, s. \N – [end{align*}]
Significado
El tiempo de viaje es extremadamente corto, como se esperaba. Dado que el cálculo se realiza íntegramente dentro de un único marco de referencia, la relatividad no interviene, aunque la velocidad del electrón sea cercana a c.
Estrategia para (b)
(b) En el marco de referencia del electrón, el tubo de vacío se mueve y el electrón está estacionario. El cátodo emisor de electrones sale del electrón y la parte frontal del tubo de vacío choca con el electrón con el mismo lugar. Por lo tanto, utilizamos la fórmula de la dilatación del tiempo para relacionar el tiempo propio en el marco de reposo del electrón con el tiempo en el marco de la televisión.
Solución
- Identificar los conocidos (de la parte a):
- Identificar la incógnita:
(\tau\_).
- Expresa la respuesta en forma de ecuación:
- Haz el cálculo:
&= 3,26 \Nveces 10^{-9}s. \end{align*}]
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), y Bill Moebs con muchos autores colaboradores. Esta obra está licenciada por OpenStax University Physics bajo una Licencia de Atribución de Creative Commons (por 4.0).
Significado
El tiempo de viaje es más corto en el marco de referencia del electrón. Como el problema requiere encontrar el intervalo de tiempo medido en diferentes marcos de referencia para un mismo proceso, la relatividad está involucrada. Si hubiéramos tratado de calcular el tiempo en el marco de reposo del electrón simplemente dividiendo los 0,200 m por la velocidad, el resultado sería ligeramente incorrecto debido a la velocidad relativista del electrón.
Ejercicio (\PageIndex{1})
¿Cuál es (\gamma\) si \(v = 0.650c\)?
Respuesta
La Paradoja de los Gemelos
Una consecuencia intrigante de la dilatación del tiempo es que un viajero espacial que se mueve a gran velocidad respecto a la Tierra envejecería menos que el gemelo terrestre del astronauta. Esto se conoce como la paradoja de los gemelos. Imaginemos que el astronauta se mueve a una velocidad tal que \(\gamma = 30,0\), como en la figura \(\PageIndex{4}\). Un viaje que tarda 2,00 años en su marco tardaría 60,0 años en el marco del gemelo terrestre. Supongamos que el astronauta viaja 1,00 año a otro sistema estelar, explora brevemente la zona y luego viaja 1,00 año de vuelta. Un astronauta que tuviera 40 años al inicio del viaje tendría 42 cuando la nave espacial regresara. Todo en la Tierra, sin embargo, habría envejecido 60,0 años. El gemelo terrestre, si todavía está vivo, tendría 100 años.
La situación le parecería diferente al astronauta de la figura (\PageIndex{4}\N). Como el movimiento es relativo, la nave espacial parecería estar inmóvil y la Tierra parecería moverse. (Esta es la sensación que se tiene cuando se vuela en un avión). Mirando por la ventana de la nave espacial, el astronauta vería que el tiempo se ralentiza en la Tierra por un factor de \ (\gamma = 30,0\). Visto desde la nave espacial, el hermano terrestre habrá envejecido sólo 2/30, o 0,07, de un año, mientras que el astronauta habría envejecido 2,00 años.
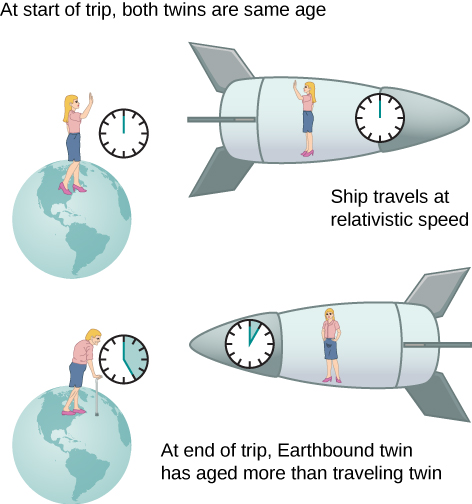
La paradoja aquí es que los dos gemelos no pueden ser correctos. Como en todas las paradojas, las conclusiones contradictorias parten de una premisa falsa. De hecho, el movimiento del astronauta es significativamente diferente al del gemelo terrestre. El astronauta acelera hasta alcanzar una gran velocidad y luego desacelera para ver el sistema estelar. Para volver a la Tierra, vuelve a acelerar y desacelerar. La nave espacial no se encuentra en un único marco inercial al que se pueda aplicar directamente la fórmula de dilatación del tiempo. Es decir, el gemelo astronauta cambia de referencias inerciales. El gemelo terrestre no experimenta estas aceleraciones y permanece en el mismo marco inercial. Por tanto, la situación no es simétrica y es incorrecto afirmar que la astronauta observa los mismos efectos que su gemelo. La falta de simetría entre los gemelos será aún más evidente cuando analicemos el viaje más adelante en este capítulo en términos de la trayectoria que sigue el astronauta a través del espacio-tiempo cuatridimensional.
En 1971, los físicos estadounidenses Joseph Hafele y Richard Keating verificaron la dilatación del tiempo a bajas velocidades relativas haciendo volar relojes atómicos extremadamente precisos alrededor del mundo en aviones comerciales. Midieron el tiempo transcurrido con una precisión de unos pocos nanosegundos y lo compararon con el tiempo medido por los relojes dejados atrás. Los resultados de Hafele y Keating estaban dentro de las incertidumbres experimentales de las predicciones de la relatividad. Había que tener en cuenta tanto la relatividad especial como la general, ya que intervenían la gravedad y las aceleraciones, así como el movimiento relativo.
Ejercicio \N(\PageIndex{2A})
a. Una partícula se desplaza a \ (1,90 \ veces 10^8 \, m/s\) y vive \ (2,1 \ veces 10^8 \, s\) cuando está en reposo respecto a un observador. ¿Cuánto tiempo vive la partícula vista en el laboratorio?
Respuesta
Ejercicio (\PageIndex{2B})
Las naves espaciales A y B pasan en direcciones opuestas a una velocidad relativa de \N(4,00 times 10^7 \, m/s\). Un reloj interno de la nave A hace que emita una señal de radio durante 1,00 s. El ordenador de la nave B corrige que el principio y el final de la señal han recorrido distancias diferentes, para calcular el intervalo de tiempo durante el cual la nave A estuvo emitiendo la señal. ¿Cuál es el intervalo de tiempo que calcula el ordenador de la nave B?
Sólo importa la velocidad relativa de las dos naves espaciales porque no hay un movimiento absoluto a través del espacio. La señal se emite desde un lugar fijo en el marco de referencia de A, por lo que el intervalo de tiempo propio de su emisión es \ (\tau = 1,00 \, s\). La duración de la señal medida desde el marco de referencia B es entonces