
En un artículo anterior, exploramos el Análisis de Regresión Lineal y su aplicación en el análisis y modelado financiero. Puede leer nuestro artículo Análisis de regresión en la modelización financiera para obtener más información sobre los conceptos estadísticos empleados en el método y dónde encuentra aplicación dentro de las finanzas.
Este artículo echará un vistazo práctico a la modelización de un modelo de Regresión Múltiple para el Producto Interior Bruto (PIB) de un país.
Antes de empezar, permítame añadir un breve descargo de responsabilidad. No soy un estadístico, y no pretendo que las variables dependientes e independientes seleccionadas sean las opciones de análisis correctas. El artículo tiene como objetivo mostrarle cómo ejecutar la Regresión múltiple en Excel e interpretar el resultado, no enseñar sobre la configuración de nuestros supuestos del modelo y la elección de las variables más apropiadas.
Ahora que tenemos esto fuera del camino y las expectativas están establecidas, ¡abramos Excel y empecemos!
Obtendremos datos públicos de Eurostat, la base de datos de estadísticas de la Comisión Europea para este ejercicio. Todos los datos fuente relevantes están dentro del archivo del modelo para su comodidad, que puede descargar a continuación. También he guardado los enlaces a las tablas de origen para explorar más a fondo si quieres.
El conjunto de datos de la UE nos da información para todos los estados miembros de la unión. Como fan masivo de Hércules Poirot de Agatha Christie, vamos a dirigir nuestra atención a Bélgica.
Como puede ver en la tabla de abajo, tenemos diecinueve observaciones de nuestra variable objetivo (PIB), así como nuestras tres variables predictoras:
- X1 – Gasto en educación en mil.
- X2 – Tasa de desempleo como % de la población activa;
- X3 – Remuneración de los empleados en mil.

Incluso antes de ejecutar nuestro modelo de regresión notamos algunas dependencias en nuestros datos. Observando la evolución a lo largo de los periodos, podemos suponer que el PIB aumenta junto con el Gasto en Educación y la Remuneración de los Empleados.
Ejecución de una Regresión Lineal Múltiple
Hay formas de calcular todos los estadísticos relevantes en Excel utilizando fórmulas. Pero es mucho más fácil con el paquete de herramientas de análisis de datos, que puedes habilitar desde la pestaña Desarrollador -> Complementos de Excel.
Busca en la pestaña Datos, y a la derecha, verás la herramienta Análisis de datos dentro de la sección Analizar.
Ejecútala y elige Regresión entre todas las opciones. Tenga en cuenta que utilizamos el mismo menú tanto para los modelos de regresión lineal simple (sencillo) como para los múltiples.
Ahora es el momento de establecer algunos rangos y configuraciones.
El Rango Y incluirá nuestra variable dependiente, el PIB. Y en el Rango X, seleccionaremos todas las columnas de la variable X. Tenga en cuenta que esto es lo mismo que ejecutar una única regresión lineal, la única diferencia es que elegimos varias columnas para X Range.
Recuerde que Excel requiere que todas las variables X estén en columnas adyacentes.
Como he seleccionado la columna Títulos, es crucial marcar la casilla de verificación de Etiquetas. Un intervalo de confianza del 95% es apropiado en la mayoría de los escenarios de análisis financiero, por lo que no lo cambiaremos.
A continuación, puede considerar colocar los datos en la misma hoja o en una nueva. Una nueva hoja de trabajo suele funcionar mejor, ya que la herramienta inserta bastantes datos.
También marcaré todas las opciones adicionales en la parte inferior. Rara vez acabo usándolas todas, pero es más fácil borrar las que no necesitamos que volver a ejecutar todo.
Suscríbase a nuestro boletín de noticias para obtener una plantilla de análisis comparativo de Excel GRATIS
Evaluación de los resultados de la regresión
Ahora que tenemos nuestro resultado resumido de Excel vamos a explorar nuestro modelo de regresión más a fondo.
La información que sacamos del módulo de Análisis de Datos de Excel comienza con las Estadísticas de Regresión.
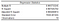
El cuadrado R es el más importante de ellos, así que podemos empezar por mirarlo. Específicamente, debemos mirar la R cuadrada ajustada en nuestro caso, ya que tenemos más de una variable X. Nos da una idea de la bondad global del ajuste.
Un R Cuadrado ajustado de 0,98 significa que nuestro modelo de regresión puede explicar alrededor del 98% de la variación de la variable dependiente Y (PIB) en torno al valor medio de las observaciones (la media de nuestra muestra). En otras palabras, el 98% de la variabilidad de ŷ (y-hat, nuestras predicciones de la variable dependiente) es captada por nuestro modelo. Un valor tan alto normalmente indicaría que podría haber algún problema con nuestro modelo. Seguiremos con nuestro modelo, pero un R Cuadrado demasiado alto puede ser problemático en un escenario de la vida real. Le sugiero que lea este artículo sobre Estadística de Jim, para aprender por qué demasiado bueno no siempre es correcto en términos de R Cuadrado.
El Error Estándar nos da una estimación de la desviación estándar del error (residuos). Generalmente, si el coeficiente es grande comparado con el error estándar, probablemente sea estadísticamente significativo.
Análisis de la Varianza (ANOVA)

La sección de Análisis de la Varianza es algo que a menudo omitimos al modelar la Regresión. Sin embargo, puede proporcionar información valiosa, y vale la pena echarle un vistazo. Puede leer más sobre la ejecución de una prueba ANOVA y ver un modelo de ejemplo en nuestro artículo dedicado.
Esta tabla nos da una prueba global de significación en los parámetros de regresión.
La columna F de la tabla ANOVA nos da la prueba F global de la hipótesis nula de que todos los coeficientes son iguales a cero. La hipótesis alternativa es que al menos uno de los coeficientes no es igual a cero. La columna F de significación nos muestra el valor p de la prueba F. Como es inferior al nivel de significación de 0,05 (con nuestro nivel de confianza del 95%), podemos rechazar la hipótesis nula de que todos los coeficientes son iguales a cero. Esto significa que nuestros parámetros de regresión no son conjuntamente insignificantes desde el punto de vista estadístico.
Puede leer más sobre las pruebas de hipótesis en nuestro artículo dedicado.
La siguiente tabla nos da información sobre los coeficientes de nuestro Modelo de Regresión Múltiple y es la parte más emocionante del análisis.

Aquí tenemos muchos detalles para el intercepto y cada uno de nuestros predictores (variables independientes). Vamos a explorar lo que representan estas columnas:
- Coeficientes – son estimaciones derivadas del método de mínimos cuadrados;
- Error estándar – la desviación estándar de las estimaciones de mínimos cuadrados;
- T-Stat – es el estadístico t para la hipótesis nula de que el coeficiente es igual a cero, frente a la hipótesis alternativa de que es diferente de cero;
- El valor P para la prueba t;
- El 95% inferior y superior definen el intervalo de confianza para los coeficientes.
Prueba de significación estadística
Es la prueba de una hipótesis nula que afirma que el coeficiente tiene una pendiente de cero. Podemos mirar los valores p para cada coeficiente y compararlos con el nivel de significación de 0,05.
Si nuestro valor p es menor que el nivel de significación, esto significa que nuestra variable independiente es estadísticamente significativa para el modelo. Al observar nuestros predictores X1 a X3, observamos que sólo X3 Remuneración de los empleados tiene un valor p inferior a 0,05, lo que significa que X1 Gasto en educación y X2 Tasa de desempleo no parecen ser estadísticamente significativos para nuestro modelo de regresión.
Como no podemos rechazar la hipótesis nula (que los coeficientes son iguales a cero), podemos eliminar X1 y X2 del modelo. También podemos confirmarlo porque el valor cero se encuentra entre los tramos de confianza inferior y superior.
Podemos decidir ejecutar el modelo sin las variables X1 y X2 y evaluar si esto da lugar a una caída significativa en la medida de R cuadrado ajustado. Si no lo hace, entonces es seguro eliminar X1 y X2 del modelo de regresión.
Si hacemos eso, obtenemos las siguientes Estadísticas de Regresión.

Podemos ver que no hay caída en el R Cuadrado, por lo que podemos eliminar con seguridad X1 y X2 de nuestro modelo y simplificarlo a una sola regresión lineal.
Residuos
Los residuos dan información sobre cuánto se desvían los puntos de datos reales (y) de los puntos de datos predichos (ŷ), basados en nuestro modelo de regresión.

Salida de la probabilidad
Esta tabla muestra los valores observados para la variable independiente (y) y los correspondientes percentiles de la muestra. Podemos calcular el primer percentil como (100 / 2 * Número de observaciones), y a partir de ahí, estos se calculan como el percentil anterior + (100 / 2).

Participaciones residuales
El análisis de Regresión Múltiple nos da una gráfica para cada variable independiente frente a los residuos. Podemos utilizar estos gráficos para evaluar si nuestros datos de la muestra se ajustan a los supuestos de la varianza para la linealidad y la homogeneidad.
La homogeneidad significa que el gráfico debe mostrar un patrón aleatorio y tener una dispersión vertical constante.
La linealidad requiere que los residuos tengan una media de cero. Podemos observar esto visualmente evaluando si los puntos se extienden aproximadamente por igual por debajo y por encima del eje x.



Plots de ajuste de líneas
El modelo nos proporciona un Plot de ajuste de líneas para cada variable independiente (predictor). Esto muestra los valores predichos (ŷ) frente a los valores observados (y). Cuanto más se acerquen, mejor predice nuestro modelo la variable dependiente en función de los regresores.



Ploteo de Probabilidad Normal
El Diagrama de Probabilidad Normal nos ayuda a determinar si los datos se ajustan a una distribución normal. Podemos añadir una Línea de Tendencia y evaluar si los puntos de datos siguen una línea recta. En nuestro caso, esto es bastante obvio, y podemos incluso no añadir la línea de tendencia.

Puedes descargar el modelo de ejemplo en Excel en el artículo original.
Limitaciones de Excel
Como Excel no es un software estadístico especializado, existen algunas limitaciones inherentes a la hora de ejecutar un modelo de regresión que debemos conocer:
- Las columnas de todos los regresores (variables independientes) tienen que ser adyacentes;
- Podemos tener hasta 16 predictores (no recuerdo dónde lo leí, así que tómalo con precaución);
- El análisis de regresión en Excel asume que el error es independiente con varianza constante (homocedasticidad);
- Si vamos por la ruta de las funciones, es crucial saber que las funciones de Excel SLOPE, INTERCEPT, y FORECAST no funcionan para la Regresión Múltiple. En cambio, TREND y LINEST funcionan de la misma manera que con un modelo de regresión simple, pero toman valores para múltiples variables X.
- y es nuestra variable dependiente;
- a es el intercepto (nuestra constante) de la estadística de regresión;
- b, c y d son los coeficientes de cada variable;
- x1 a x3 son las variables independientes (nuestros regresores o predictores);
- ɛ es el error o residuos, que a menudo podemos excluir.
Conclusión
Empezamos con tres variables independientes, realizamos un análisis de regresión, e identificamos que dos predictores no tienen significación estadística para nuestro modelo.
Entonces eliminamos esos para terminar con un modelo de Regresión Lineal Simple.
Una vez que esté satisfecho con su modelo puede construir su ecuación de regresión, como hemos discutido en otros artículos. Con esta ecuación puedes entonces pronosticar la variable dependiente para el futuro.
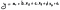
Donde:
Tenga en cuenta que este artículo pretende ilustrar los conceptos de la ejecución de un Análisis de Regresión Múltiple en Excel. Trata de explicar en qué debemos centrarnos a la hora de evaluar los resultados. Todo buen modelo comienza con el establecimiento de suposiciones y expectativas razonables, en las que no soy un experto, por lo que no afirmo que las variables dependientes e independientes elegidas hayan sido las correctas.
¡Gracias por leer! Puedes mostrar tu apoyo compartiendo este artículo con colegas y amigos.