Mostrar aviso para móviles Mostrar todas las notas Ocultar todas las notas
Sección 1-12 : Coordenadas cilíndricas
Al igual que en el espacio bidimensional, el sistema de coordenadas estándar \a la izquierda( {x,y,z} \a la derecha)\a se denomina sistema de coordenadas cartesianas. En las dos últimas secciones de este capítulo veremos algunos sistemas de coordenadas alternativos para el espacio tridimensional.
Comenzaremos con el sistema de coordenadas cilíndricas. Este es bastante sencillo ya que no es más que una extensión de las coordenadas polares a las tres dimensiones. No sólo es una extensión de las coordenadas polares, sino que lo extendemos a la tercera dimensión igual que extendemos las coordenadas cartesianas a la tercera dimensión. Lo único que hacemos es añadir una \(z\) como tercera coordenada. Las coordenadas \(r\) y \theta) son las mismas que con las coordenadas polares.
Aquí tenemos un croquis de un punto en \({\mathbb{R}^3}).
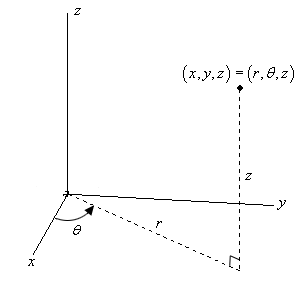
Las conversiones para \(x\) y \(y\) son las mismas conversiones que usamos cuando veíamos las coordenadas polares. Por tanto, si tenemos un punto en coordenadas cilíndricas, las coordenadas cartesianas se pueden encontrar utilizando las siguientes conversiones.
La tercera ecuación es sólo un reconocimiento de que la coordenada \N-(z\) de un punto en coordenadas cartesianas y polares es la misma.
Así mismo, si tenemos un punto en coordenadas cartesianas, las coordenadas cilíndricas se pueden encontrar utilizando las siguientes conversiones.
- (r = 5\)
- ({r^2} + {z^2} = 100\)
- (z = r\)
Mostrar todas las soluciones Ocultar todas las soluciones
En dos dimensiones sabemos que se trata de un círculo de radio 5. Como ahora estamos en tres dimensiones y no hay \(z\) en la ecuación esto significa que se permite que varíe libremente. Por tanto, para cualquier \(z\) dado tendremos un círculo de radio 5 centrado en el eje \(z\)
En otras palabras, tendremos un cilindro de radio 5 centrado en el eje \(z\).
b \N({r^2} + {z^2} = 100\) Mostrar solución
Esta ecuación será fácil de identificar una vez que la convirtamos de nuevo a coordenadas cartesianas.
Así pues, se trata de una esfera centrada en el origen con radio 10.
De nuevo, esta no será tan mala si la convertimos de nuevo a cartesianas. Por razones que serán evidentes en algún momento, primero elevaremos al cuadrado ambos lados y luego haremos la conversión.
Desde la sección de superficies cuádricas sabemos que ésta es la ecuación de un cono.