Mecánica de materiales
Ecuaciones y aplicaciones del esfuerzo cortante
Esfuerzo cortante general:
La fórmula para calcular el esfuerzo cortante medio es:
donde τ = el esfuerzo cortante; F = la fuerza aplicada; A = el área de la sección transversal del material con área perpendicular al vector fuerza aplicada;
Corte de viga:
El corte de viga se define como el esfuerzo cortante interno de una viga causado por la fuerza cortante aplicada a la viga.
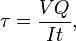donde V = fuerza de corte total en el lugar en cuestión; Q = momento estático del área; t = espesor en el material perpendicular al corte; I = momento de inercia de toda el área transversal. Esta fórmula también se conoce como la fórmula de Jourawski.Esfuerzos de cizallamiento semimonocascoLos esfuerzos de cizallamiento dentro de una estructura semimonocasco pueden calcularse idealizando la sección transversal de la estructura en un conjunto de largueros (que soportan sólo cargas axiales) y bandas (que soportan sólo flujos de cizallamiento). Dividiendo el flujo de cizalladura por el espesor de una parte determinada de la estructura semimonocasco se obtiene el esfuerzo de cizalladura. Por lo tanto, el esfuerzo cortante máximo se producirá en el alma del flujo cortante máximo o en el espesor mínimo, el peso de una presa o un dique rellenos de tierra puede provocar el colapso del subsuelo, como si se tratara de un pequeño corrimiento de tierras.Cizallamiento por impactoLa tensión máxima de cizallamiento creada en una barra redonda sólida sometida a un impacto viene dada por la ecuación:
donde U = cambio de energía cinética; G = módulo de cizallamiento; V = volumen de la barra; y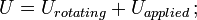 
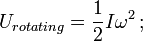
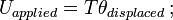
= momento de inercia de la masa; ω = velocidad angular.
Esfuerzo cortante en fluidos:
Cualquier fluido real (líquidos y gases incluidos) que se mueva a lo largo de una frontera sólida incurrirá en un esfuerzo cortante en dicha frontera. La condición de no deslizamiento dicta que la velocidad del fluido en la frontera (relativa a la frontera) es cero, pero a cierta altura de la frontera la velocidad del flujo debe ser igual a la del fluido. La región comprendida entre estos dos puntos recibe el nombre de capa límite. Para todos los fluidos newtonianos en flujo laminar, el esfuerzo cortante es proporcional a la velocidad de deformación del fluido, siendo la viscosidad la constante de proporcionalidad. Sin embargo, en el caso de los fluidos no newtonianos, esto ya no es así, ya que en estos fluidos la viscosidad no es constante. El esfuerzo de cizallamiento se produce en la frontera como resultado de esta pérdida de velocidad. El esfuerzo cortante, para un fluido newtoniano, en un elemento de superficie paralelo a una placa plana, en el punto y, viene dado por:
donde μ es la viscosidad dinámica del fluido; u es la velocidad del fluido a lo largo de la frontera; y es la altura sobre la frontera. En concreto, el esfuerzo cortante de la pared se define como: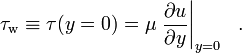 
En caso de viento, el esfuerzo cortante en la frontera se denomina esfuerzo del viento.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Netherlands, pp. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (enero de 1987), «Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow», NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), «Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars», AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), «Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³», International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008