Los comandos clave de MATLAB utilizados en este tutorial son: tf , step , pid , feedback , pidtune
Resumen del PID
En este tutorial, consideraremos el siguiente sistema de retroalimentación unitaria:
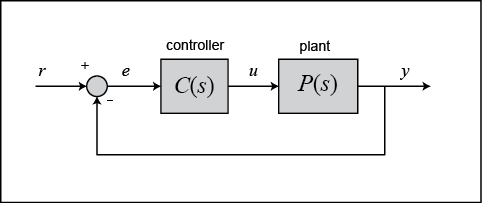
La salida de un controlador PID, que es igual a la entrada de control a la planta, se calcula en el dominio del tiempo a partir del error de realimentación como sigue:
(1)
En primer lugar, veamos cómo funciona el controlador PID en un sistema de lazo cerrado utilizando el esquema mostrado anteriormente. La variable ( ) representa el error de seguimiento, la diferencia entre la salida deseada (
) representa el error de seguimiento, la diferencia entre la salida deseada ( ) y la salida real (
) y la salida real ( ). Esta señal de error (
). Esta señal de error ( ) se alimenta al controlador PID, y el controlador calcula tanto la derivada como la integral de esta señal de error con respecto al tiempo. La señal de control (
) se alimenta al controlador PID, y el controlador calcula tanto la derivada como la integral de esta señal de error con respecto al tiempo. La señal de control ( ) para la planta es igual a la ganancia proporcional (
) para la planta es igual a la ganancia proporcional ( ) por la magnitud del error más la ganancia integral (
) por la magnitud del error más la ganancia integral ( ) por la integral del error más la ganancia derivativa (
) por la integral del error más la ganancia derivativa ( ) por la derivada del error.
) por la derivada del error.
Esta señal de control ( ) se introduce en la planta y se obtiene la nueva salida (
) se introduce en la planta y se obtiene la nueva salida ( ). La nueva salida (
). La nueva salida ( ) se retroalimenta y se compara con la referencia para encontrar la nueva señal de error (
) se retroalimenta y se compara con la referencia para encontrar la nueva señal de error ( ). El controlador toma esta nueva señal de error y calcula una actualización de la entrada de control. Este proceso continúa mientras el controlador está en funcionamiento.
). El controlador toma esta nueva señal de error y calcula una actualización de la entrada de control. Este proceso continúa mientras el controlador está en funcionamiento.
La función de transferencia de un controlador PID se encuentra tomando la transformada de Laplace de la ecuación (1).
(2)
donde  = ganancia proporcional,
= ganancia proporcional,  = ganancia integral, y
= ganancia integral, y  = ganancia derivativa.
= ganancia derivativa.
Podemos definir un controlador PID en MATLAB utilizando un modelo de función de transferencia directamente, por ejemplo:
Kp = 1;Ki = 1;Kd = 1;s = tf('s');C = Kp + Ki/s + Kd*s
C = s^2 + s + 1 ----------- s Continuous-time transfer function.
Alternativamente, podemos utilizar el objeto pid de MATLAB para generar un controlador de tiempo continuo equivalente como sigue:
C = pid(Kp,Ki,Kd)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.
Convirtamos el objeto pid en una función de transferencia para comprobar que da el mismo resultado que el anterior:
tf(C)
ans = s^2 + s + 1 ----------- s Continuous-time transfer function.
Las características de los términos P, I y D
Aumentar la ganancia proporcional ( ) tiene el efecto de aumentar proporcionalmente la señal de control para el mismo nivel de error. El hecho de que el controlador «empuje» más fuerte para un nivel de error dado tiende a hacer que el sistema de lazo cerrado reaccione más rápidamente, pero también a sobrepasar más. Otro efecto de aumentar
) tiene el efecto de aumentar proporcionalmente la señal de control para el mismo nivel de error. El hecho de que el controlador «empuje» más fuerte para un nivel de error dado tiende a hacer que el sistema de lazo cerrado reaccione más rápidamente, pero también a sobrepasar más. Otro efecto de aumentar  es que tiende a reducir, pero no a eliminar, el error de estado estacionario.
es que tiende a reducir, pero no a eliminar, el error de estado estacionario.
La adición de un término derivativo al controlador ( ) añade la capacidad del controlador de «anticipar» el error. Con un control proporcional simple, si
) añade la capacidad del controlador de «anticipar» el error. Con un control proporcional simple, si  es fijo, la única manera de que el control aumente es si el error aumenta. Con el control derivativo, la señal de control puede llegar a ser grande si el error comienza a inclinarse hacia arriba, incluso mientras la magnitud del error es todavía relativamente pequeña. Esta anticipación tiende a añadir amortiguación al sistema, disminuyendo así el sobreimpulso. La adición de un término derivativo, sin embargo, no tiene ningún efecto sobre el error de estado estacionario.
es fijo, la única manera de que el control aumente es si el error aumenta. Con el control derivativo, la señal de control puede llegar a ser grande si el error comienza a inclinarse hacia arriba, incluso mientras la magnitud del error es todavía relativamente pequeña. Esta anticipación tiende a añadir amortiguación al sistema, disminuyendo así el sobreimpulso. La adición de un término derivativo, sin embargo, no tiene ningún efecto sobre el error de estado estacionario.
La adición de un término integral al controlador ( ) tiende a ayudar a reducir el error de estado estacionario. Si hay un error persistente y constante, el integrador se acumula y se acumula, aumentando así la señal de control y conduciendo el error hacia abajo. Un inconveniente del término integral, sin embargo, es que puede hacer que el sistema sea más lento (y oscilatorio), ya que cuando la señal de error cambia de signo, el integrador puede tardar un tiempo en «desenrollarse.»
) tiende a ayudar a reducir el error de estado estacionario. Si hay un error persistente y constante, el integrador se acumula y se acumula, aumentando así la señal de control y conduciendo el error hacia abajo. Un inconveniente del término integral, sin embargo, es que puede hacer que el sistema sea más lento (y oscilatorio), ya que cuando la señal de error cambia de signo, el integrador puede tardar un tiempo en «desenrollarse.»
Los efectos generales de cada parámetro del controlador (

 ) en un sistema de lazo cerrado se resumen en la siguiente tabla. Tenga en cuenta que estas directrices son válidas en muchos casos, pero no en todos. Si realmente quiere conocer el efecto de la sintonización de las ganancias individuales, tendrá que hacer más análisis, o tendrá que realizar pruebas en el sistema real.
) en un sistema de lazo cerrado se resumen en la siguiente tabla. Tenga en cuenta que estas directrices son válidas en muchos casos, pero no en todos. Si realmente quiere conocer el efecto de la sintonización de las ganancias individuales, tendrá que hacer más análisis, o tendrá que realizar pruebas en el sistema real.
| |
| |
|
|
|
Problema de ejemplo
Supongamos que tenemos un sencillo sistema masa-muelle-amortiguador sencillo.

La ecuación de gobierno de este sistema es
(3)
Tomando la transformada de Laplace de la ecuación de gobierno, obtenemos
(4)
La función de transferencia entre la fuerza de entrada  y el desplazamiento de salida
y el desplazamiento de salida  se convierte entonces en
se convierte entonces en
(5)
Dejemos
m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N
Sustituir estos valores en la función de transferencia anterior
(6)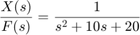
El objetivo de este problema es mostrar cómo cada uno de los términos, 
 , y
, y  , contribuye a obtener los objetivos comunes de:
, contribuye a obtener los objetivos comunes de:
- Tiempo de subida rápido
- Superación mínima
- Error de estado estacionario cero
Respuesta al escalón en lazo abierto
Veamos primero la respuesta al escalón en lazo abierto. Cree un nuevo archivo m y ejecute el siguiente código:
s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)
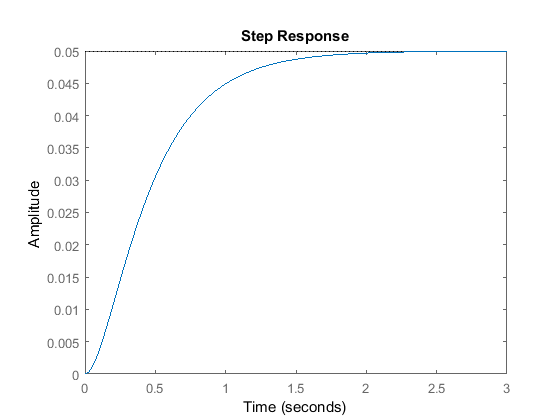
La ganancia DC de la función de transferencia de la planta es 1/20, por lo que 0,05 es el valor final de la salida a una entrada de paso unitaria. Esto corresponde a un error en estado estacionario de 0,95, que es bastante grande. Además, el tiempo de subida es de aproximadamente un segundo, y el tiempo de estabilización es de aproximadamente 1,5 segundos. Diseñemos un controlador que reduzca el tiempo de subida, reduzca el tiempo de asentamiento y elimine el error de estado estacionario.
Control proporcional
A partir de la tabla mostrada anteriormente, vemos que el controlador proporcional ( ) reduce el tiempo de subida, aumenta el sobreimpulso y reduce el error de estado estacionario.
) reduce el tiempo de subida, aumenta el sobreimpulso y reduce el error de estado estacionario.
La función de transferencia en lazo cerrado de nuestro sistema de retroalimentación unitaria con un controlador proporcional es la siguiente, donde  es nuestra salida (igual a
es nuestra salida (igual a  ) y nuestra referencia
) y nuestra referencia  es la entrada:
es la entrada:
(7)
Deje que la ganancia proporcional ( ) sea igual a 300 y cambie el m-archivo por lo siguiente:
) sea igual a 300 y cambie el m-archivo por lo siguiente:
Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.
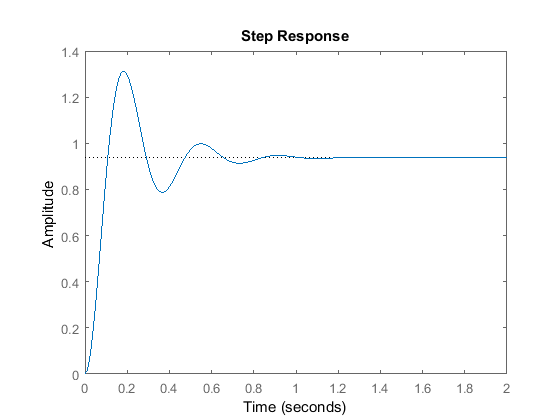
El gráfico anterior muestra que el controlador proporcional redujo tanto el tiempo de subida como el error de estado estacionario, aumentó el sobreimpulso y disminuyó el tiempo de establecimiento en una pequeña cantidad.
Control Proporcional-Derivativo
Ahora, echemos un vistazo al control PD. A partir de la tabla mostrada anteriormente, vemos que la adición de control derivativo ( ) tiende a reducir tanto el sobreimpulso como el tiempo de establecimiento. La función de transferencia en lazo cerrado del sistema dado con un controlador PD es:
) tiende a reducir tanto el sobreimpulso como el tiempo de establecimiento. La función de transferencia en lazo cerrado del sistema dado con un controlador PD es:
(8)
Deja que  sea igual a 300 como antes y deja que
sea igual a 300 como antes y deja que  sea igual a 10. Introduzca los siguientes comandos en un archivo m y ejecútelo en la ventana de comandos de MATLAB.
sea igual a 10. Introduzca los siguientes comandos en un archivo m y ejecútelo en la ventana de comandos de MATLAB.
Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.
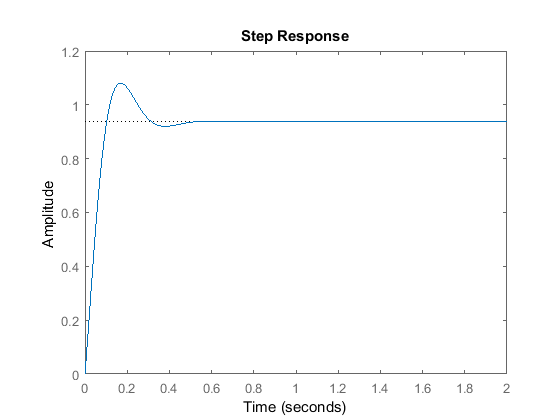
Este gráfico muestra que la adición del término de la derivada redujo tanto el sobreimpulso como el tiempo de asentamiento, y tuvo un efecto insignificante en el tiempo de subida y el error de estado estacionario.
Control Proporcional-Integral
Antes de proceder al control PID, vamos a investigar el control PI. A partir de la tabla, vemos que la adición de control integral ( ) tiende a disminuir el tiempo de subida, a aumentar tanto el sobreimpulso como el tiempo de estabilización, y a reducir el error de estado estacionario. Para el sistema dado, la función de transferencia en lazo cerrado con un controlador PI es:
) tiende a disminuir el tiempo de subida, a aumentar tanto el sobreimpulso como el tiempo de estabilización, y a reducir el error de estado estacionario. Para el sistema dado, la función de transferencia en lazo cerrado con un controlador PI es:
(9)
Reduzcamos  a 30, y dejemos que
a 30, y dejemos que  sea igual a 70. Crea un nuevo archivo m e introduce los siguientes comandos.
sea igual a 70. Crea un nuevo archivo m e introduce los siguientes comandos.
Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.
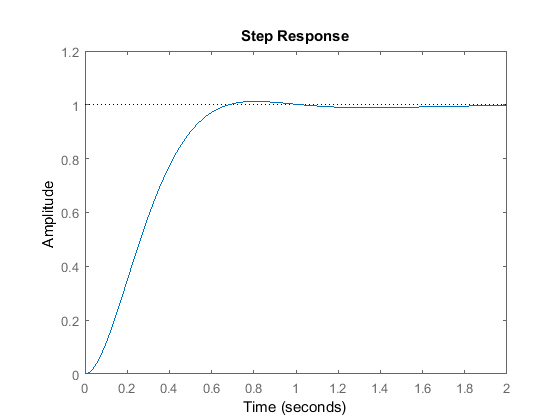
Ejecute este archivo m en la ventana de comandos de MATLAB y debería generar el gráfico anterior. Hemos reducido la ganancia proporcional ( ) porque el controlador integral también reduce el tiempo de subida y aumenta el sobreimpulso como lo hace el controlador proporcional (doble efecto). La respuesta anterior muestra que el controlador integral eliminó el error de estado estacionario en este caso.
) porque el controlador integral también reduce el tiempo de subida y aumenta el sobreimpulso como lo hace el controlador proporcional (doble efecto). La respuesta anterior muestra que el controlador integral eliminó el error de estado estacionario en este caso.
Control Proporcional-Integral-Derivado
Ahora, examinemos el control PID. La función de transferencia en lazo cerrado del sistema dado con un controlador PID es:
(10)
Tras varias iteraciones de ajuste, las ganancias 
 = 300, y
= 300, y  = 50 proporcionaron la respuesta deseada. Para confirmarlo, introduzca los siguientes comandos en un archivo m y ejecútelo en la ventana de comandos. Debería obtener la siguiente respuesta de paso.
= 50 proporcionaron la respuesta deseada. Para confirmarlo, introduzca los siguientes comandos en un archivo m y ejecútelo en la ventana de comandos. Debería obtener la siguiente respuesta de paso.
Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.
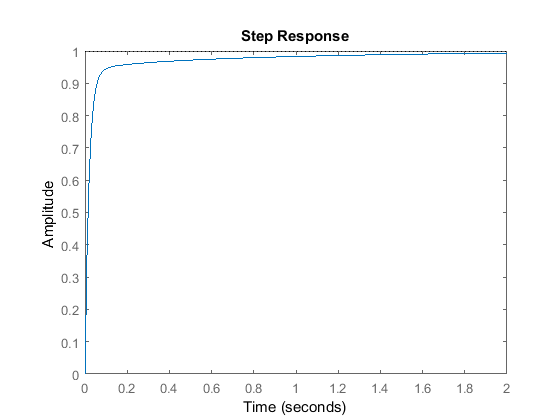
Ahora, hemos diseñado un sistema de lazo cerrado sin sobreimpulso, con tiempo de subida rápido y sin error de estado estacionario.
Consejos generales para diseñar un controlador PID
Cuando esté diseñando un controlador PID para un sistema determinado, siga los pasos que se muestran a continuación para obtener una respuesta deseada.
- Obtenga una respuesta en lazo abierto y determine lo que debe mejorarse
- Añada un control proporcional para mejorar el tiempo de subida
- Añada un control derivado para reducir el sobreimpulso
- Añada un control integral para reducir el error de estado estacionario
- Añada un control integral para reducir el error de estado estacionario
- .error de estado estable
- Ajuste cada una de las ganancias

 , y
, y  hasta obtener una respuesta global deseada. Siempre puede consultar la tabla que se muestra en esta página de «Tutorial PID» para saber qué controlador controla cada característica.
hasta obtener una respuesta global deseada. Siempre puede consultar la tabla que se muestra en esta página de «Tutorial PID» para saber qué controlador controla cada característica.
Por último, tenga en cuenta que no es necesario implementar los tres controladores (proporcional, derivativo e integral) en un solo sistema, si no es necesario. Por ejemplo, si un controlador PI cumple con los requisitos dados (como el ejemplo anterior), entonces usted no necesita implementar un controlador derivativo en el sistema. Mantenga el controlador tan simple como sea posible.
Un ejemplo de ajuste de un controlador PI en un sistema físico real se puede encontrar en el siguiente enlace. Este ejemplo también comienza a ilustrar algunos desafíos de la implementación del control, incluyendo: la saturación del control, el wind-up del integrador y la amplificación del ruido.
Sintonización automática del PID
MATLAB proporciona herramientas para elegir automáticamente las ganancias óptimas del PID, lo que hace innecesario el proceso de prueba y error descrito anteriormente. Puede acceder al algoritmo de sintonización directamente usando pidtune o a través de una bonita interfaz gráfica de usuario (GUI) usando pidTuner.
El algoritmo de ajuste automatizado de MATLAB elige las ganancias del PID para equilibrar el rendimiento (tiempo de respuesta, ancho de banda) y la robustez (márgenes de estabilidad). Por defecto, el algoritmo diseña para un margen de fase de 60 grados.
Exploremos estas herramientas automatizadas generando primero un controlador proporcional para el sistema masa-muelle-amortiguador introduciendo el comando que se muestra a continuación. En la sintaxis mostrada, P es el modelo de planta generado previamente, y ‘p’ especifica que el sintonizador emplea un controlador proporcional.
pidTuner(P,'p')
Debería aparecer la ventana GUI del pidTuner, como la que se muestra a continuación.
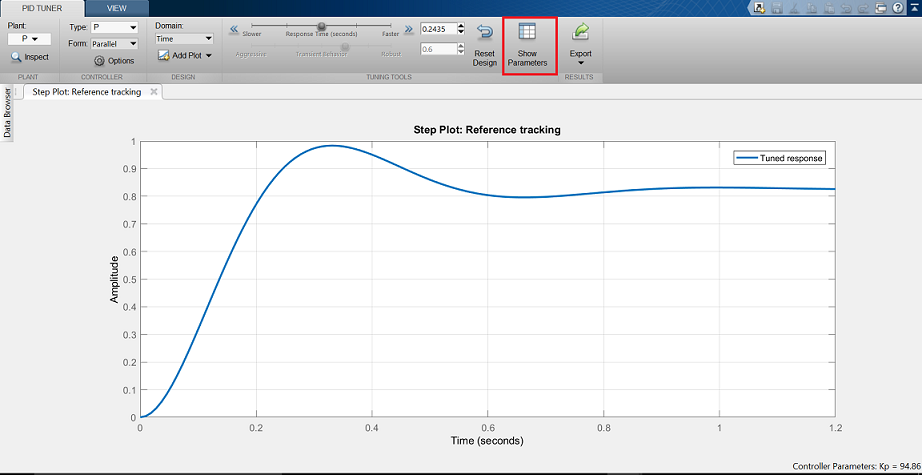
Nota que la respuesta al escalón mostrada es más lenta que la del controlador proporcional que diseñamos a mano. Ahora haz clic en el botón Mostrar parámetros de la parte superior derecha. Como era de esperar, la ganancia proporcional,  , es menor que la que empleamos,
, es menor que la que empleamos,  < 300.
< 300.
Ahora podemos ajustar interactivamente los parámetros del controlador y ver inmediatamente la respuesta resultante en la ventana de la interfaz gráfica de usuario. Prueba a arrastrar el deslizador de Tiempo de respuesta hacia la derecha hasta 0,14 s, como se muestra en la figura siguiente. Esto hace que la respuesta se acelere, y podemos ver que  está ahora más cerca del valor elegido manualmente. También podemos ver otros parámetros de rendimiento y robustez del sistema. Observe que antes de ajustar el deslizador, el margen de fase objetivo era de 60 grados. Este es el valor por defecto del pidTuner y generalmente proporciona un buen equilibrio entre robustez y rendimiento.
está ahora más cerca del valor elegido manualmente. También podemos ver otros parámetros de rendimiento y robustez del sistema. Observe que antes de ajustar el deslizador, el margen de fase objetivo era de 60 grados. Este es el valor por defecto del pidTuner y generalmente proporciona un buen equilibrio entre robustez y rendimiento.

Ahora vamos a intentar diseñar un controlador PID para nuestro sistema. Especificando el controlador previamente diseñado o (línea base), C, como segundo parámetro, pidTuner diseñará otro controlador PID (en lugar de P o PI) y comparará la respuesta del sistema con el controlador automatizado con la de la línea base.
pidTuner(P,C)
Vemos en la ventana de salida que el controlador automatizado responde más lentamente y muestra más sobreimpulso que la línea base. Ahora elija la opción Dominio: Frecuencia de la barra de herramientas, que revela los parámetros de ajuste del dominio de la frecuencia.
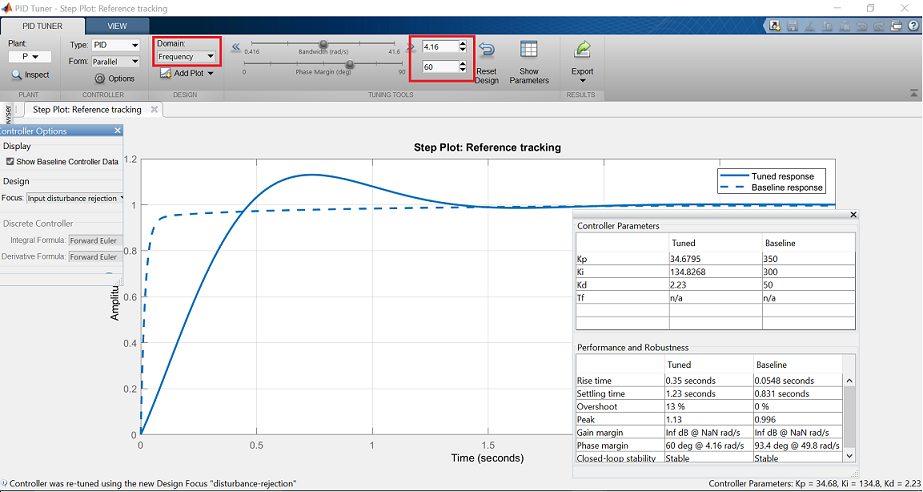
Ahora introduzca 32 rad/s para el ancho de banda y 90 grados para el margen de fase, para generar un controlador similar en rendimiento a la línea de base. Tenga en cuenta que un mayor ancho de banda de lazo cerrado resulta en un tiempo de subida más rápido, y un mayor margen de fase reduce el sobreimpulso y mejora la estabilidad del sistema.
Por último, observamos que podemos generar el mismo controlador utilizando la herramienta de línea de comandos pidtune en lugar de la GUI pidTuner empleando la siguiente sintaxis.
opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90
Publicado con MATLAB® 9.2