Los cálculos del PPT se realizan en el calibre E, lo que significa que el campo láser se toma como ondas electromagnéticas. La tasa de ionización también puede ser calculada en el calibre A, que enfatiza la naturaleza de partícula de la luz (absorbiendo múltiples fotones durante la ionización). Este enfoque fue adoptado por el modelo Krainov basado en los trabajos anteriores de Faisal y Reiss. La tasa resultante viene dada por
W K R A = ∑ n = N ∞ 2 π ω 2 p ( n – n o s c ) 2 ∫ d Ω | F T ( I K A R Ψ ( r ) ) | 2 J n 2 ( n f , n o s c 2 ) {\displaystyle W_{KRA}={suma _{n=N}^{infty }2\pi \omega ^{2}p\left(n-n_{mathrm {osc} }\right)^{2}int \mathrm {d} \ {{Omega \}} {{I}} {{Psi \}} {{I}} {{Mathbf \}} {{D}}} {{D}}} {{2}J{{{n}^{2}} {{N}},{{Frac {{Mathrm}} {{2}} {{D}}}

donde:
- n i = E i / ω , {\displaystyle n_{i}=E_{i}/\omega ,}
- n o s c = U p / ω {{displaystyle n_{mathrm {osc}} }=U_{p}/\omega }
con U p {\displaystyle U_{p}}
siendo la energía ponderomotriz,
- N = {\displaystyle N=}
es el número mínimo de fotones necesarios para ionizar el átomo,
- J n ( u , v ) {{displaystyle J_{n}(u,v)}
es la función de Bessel doble,
- p = 2 ω ( n – n o s c – n i ) , {{displaystyle p={sqrt {2\omega (n-n_{mathrm {osc} }-n_{i})}},
- n f = 2 n o s c / ω p cos ( θ ) {\displaystyle n_{f}=2{sqrt {n_{mathrm {osc}}/{omega}}. }/\omega }}p\cos(\theta )}
con θ {\displaystyle \theta }
el ángulo entre el momento del electrón, p, y el campo eléctrico del láser, F,
- FT es la transformada de Fourier tridimensional, y
- I K A R = ( 2 Z 2 n 2 F r ) n {\displaystyle I_{KAR}=left({\frac {2Z^{2}}{n^{2}Fr}}right)^{n}}
incorpora la corrección de Coulomb en el modelo SFA.
Estabilización atómica/atrapamiento de la población
En el cálculo de la tasa de MPI de los átomos sólo se consideran las transiciones a los estados del continuo. Esta aproximación es aceptable siempre y cuando no haya resonancia multifotónica entre el estado básico y algunos estados excitados. Sin embargo, en la situación real de la interacción con láseres pulsados, durante la evolución de la intensidad del láser, debido al diferente desplazamiento de Stark de los estados básico y excitado, existe la posibilidad de que algún estado excitado entre en resonancia multifotónica con el estado básico. Dentro de la imagen del átomo vestido, el estado de tierra vestido por m

fotones y el estado resonante sufren un cruce evitado a la intensidad de resonancia I r {\displaystyle I_{r}}

. La distancia mínima, V m {\displaystyle V_{m}}
 , en el cruce evitado es proporcional a la frecuencia Rabi generalizada, Γ ( t ) = Γ m I ( t ) m / 2 {\displaystyle \Gamma (t)=\Gamma _{m}I(t)^{m/2}}
, en el cruce evitado es proporcional a la frecuencia Rabi generalizada, Γ ( t ) = Γ m I ( t ) m / 2 {\displaystyle \Gamma (t)=\Gamma _{m}I(t)^{m/2}}

acoplando los dos estados. De acuerdo con Story et al., la probabilidad de permanecer en el estado básico, P g {displaystyle P_{g}}

, viene dada por P g = exp ( – 2 π W m 2 d W / d t ) {{displaystyle P_{g}=exp \left(-{frac {2\pi W_{m}^{2}}{mathrm {d} W/{mathrm {d} t}}right)}

donde W {{displaystyle W}}

es la diferencia de energía dependiente del tiempo entre los dos estados vestidos. En la interacción con un pulso corto, si la resonancia dinámica se alcanza en la parte ascendente o descendente del pulso, la población prácticamente se mantiene en el estado básico y se puede despreciar el efecto de las resonancias multifotónicas. Sin embargo, si los estados entran en resonancia en el pico del pulso, donde d W / d t = 0 {\displaystyle \mathrm {d} W/\mathrm {d} t=0}

, entonces el estado excitado está poblado. Una vez poblado, como el potencial de ionización del estado excitado es pequeño, se espera que el electrón se ionice instantáneamente.
En 1992, de Boer y Muller demostraron que los átomos de Xe sometidos a pulsos cortos de láser podían sobrevivir en los estados altamente excitados 4f, 5f y 6f . Se creía que estos estados habían sido excitados por el cambio dinámico de Stark de los niveles en resonancia multifotónica con el campo durante la parte ascendente del pulso láser. La evolución posterior del pulso láser no ionizó completamente estos estados, dejando atrás algunos átomos altamente excitados. Nos referiremos a este fenómeno como «atrapamiento de población».

Mencionamos el cálculo teórico de que la ionización incompleta se produce siempre que hay una excitación resonante paralela en un nivel común con pérdida de ionización. Consideramos un estado como el 6f de Xe que consta de 7 niveles cuasi-degenerados en el rango del ancho de banda del láser. Estos niveles junto con el continuo constituyen un sistema lambda. El mecanismo del atrapamiento de tipo lambda se presenta esquemáticamente en la figura. En la parte ascendente del pulso (a), el estado excitado (con dos niveles degenerados 1 y 2) no está en resonancia multifotónica con el estado básico. El electrón se ioniza a través del acoplamiento multifotónico con el continuo. Al aumentar la intensidad del pulso, el estado excitado y el continuo se desplazan en energía debido al desplazamiento de Stark. En el pico del pulso (b), los estados excitados entran en resonancia multifotónica con el estado de tierra. Cuando la intensidad comienza a disminuir (c), los dos estados se acoplan a través del continuo y la población queda atrapada en una superposición coherente de los dos estados. Bajo la acción posterior del mismo pulso, debido a la interferencia en las amplitudes de transición del sistema lambda, el campo no puede ionizar la población completamente y una fracción de la población quedará atrapada en una superposición coherente de los niveles cuasi degenerados. Según esta explicación, los estados con mayor momento angular -con más subniveles- tendrían una mayor probabilidad de atrapar a la población. En general, la fuerza del atrapamiento vendrá determinada por la fuerza del acoplamiento de dos fotones entre los niveles cuasi degenerados a través del continuo. En 1996, utilizando un láser muy estable y minimizando los efectos de enmascaramiento de la expansión de la región focal con el aumento de la intensidad, Talebpour et al. observaron estructuras en las curvas de iones con carga simple de Xe, Kr y Ar. Estas estructuras se atribuyeron al atrapamiento de electrones en el fuerte campo láser. Una demostración más inequívoca del atrapamiento de la población ha sido comunicada por T. Morishita y C. D. Lin.
Ionización múltiple no secuencialEditar
El fenómeno de la ionización no secuencial (NSI) de los átomos expuestos a campos láser intensos ha sido objeto de muchos estudios teóricos y experimentales desde 1983. Los trabajos pioneros se iniciaron con la observación de una estructura de «rodilla» en la curva de señal de iones Xe2+ frente a la intensidad por parte de L’Huillier et al. Desde el punto de vista experimental, la doble ionización NS se refiere a procesos que de alguna manera aumentan la tasa de producción de iones de doble carga por un factor enorme a intensidades inferiores a la intensidad de saturación del ion de carga simple. Muchos, en cambio, prefieren definir la NSI como un proceso por el que se ionizan dos electrones casi simultáneamente. Esta definición implica que además del canal secuencial A + L – > A + + L – > A + + {\displaystyle A+L->A^{+}+L->A^{++}

A^{++}

que es la principal contribución a la producción de iones de doble carga a intensidades más bajas. La primera observación de NSI triple en argón interactuando con un láser de 1 µm fue reportada por Augst et al. Más tarde, estudiando sistemáticamente el NSI de todos los átomos de gases raros, se observó el NSI cuádruple de Xe. La conclusión más importante de este estudio fue la observación de la siguiente relación entre la tasa de NSI a cualquier estado de carga y la tasa de ionización túnel (predicha por la fórmula ADK) a los estados de carga anteriores; W N S ( A n + ) = ∑ i = 1 n – 1 α n ( λ ) W A D K ( A i + ) {{displaystyle W_{NS}(A^{n+})={suma _{i=1}^{n-1}{alfa _{n}}{izquierda(\lambda{derecha)} W_{ADK}{izquierda(A^{i+}{derecha)}

donde W A D K ( A i + ) {{displaystyle W_{ADK} {{dirección}}(A^{i+} {dirección)}

es la tasa de tunelización cuasiestática hacia el estado de carga i’s y α n ( λ ) {{displaystyle \a alfa _{n}(\a lambda )}

son unas constantes que dependen de la longitud de onda del láser (pero no de la duración del pulso).
Se han propuesto dos modelos para explicar la ionización no secuencial; el modelo de sacudida y el modelo de redistribución de electrones. El modelo de sacudida (SO), propuesto por primera vez por Fittinghoff et al., se adopta del campo de la ionización de átomos por rayos X y proyectiles de electrones, donde el proceso SO es uno de los principales mecanismos responsables de la ionización múltiple de los átomos. El modelo SO describe el proceso NS como un mecanismo en el que un electrón es ionizado por el campo láser y la salida de este electrón es tan rápida que los electrones restantes no tienen tiempo suficiente para ajustarse a los nuevos estados de energía. Por lo tanto, existe una cierta probabilidad de que, tras la ionización del primer electrón, un segundo electrón sea excitado a estados con mayor energía (shake-up) o incluso ionizado (shake-off). Debemos mencionar que, hasta ahora, no ha habido ningún cálculo cuantitativo basado en el modelo SO, y el modelo sigue siendo cualitativo.
El modelo de rescate de electrones fue desarrollado independientemente por Kuchiev, Schafer et al, Corkum, Becker y Faisal y Faisal y Becker. Las principales características del modelo pueden entenderse fácilmente a partir de la versión de Corkum. El modelo de Corkum describe la ionización de la NS como un proceso en el que un electrón se ioniza por túnel. A continuación, el electrón interactúa con el campo láser, donde es acelerado lejos del núcleo nuclear. Si el electrón se ha ionizado en una fase adecuada del campo, pasará por la posición del ion restante medio ciclo más tarde, donde puede liberar un electrón adicional por impacto electrónico. Sólo la mitad de las veces el electrón se libera con la fase adecuada y la otra mitad nunca vuelve al núcleo nuclear. La energía cinética máxima que puede tener el electrón que regresa es 3,17 veces el potencial ponderomotor ( U p {displaystyle U_{p}}

) del láser. El modelo de Corkum pone un límite de corte a la intensidad mínima ( U p {\displaystyle U_{p}}

es proporcional a la intensidad) donde puede producirse la ionización debida a la redistribución.
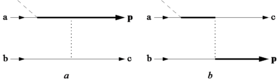
El modelo de re-dispersión en la versión de Kuchiev (modelo de Kuchiev) es mecánico cuántico. La idea básica del modelo se ilustra con los diagramas de Feynman de la figura a. Primero ambos electrones están en el estado básico de un átomo. Las líneas marcadas con a y b describen los estados atómicos correspondientes. A continuación, el electrón a se ioniza. El comienzo del proceso de ionización se muestra mediante la intersección con una línea discontinua inclinada. donde se produce el MPI. La propagación del electrón ionizado en el campo láser, durante la cual absorbe otros fotones (ATI), se muestra mediante la línea gruesa completa. La colisión de este electrón con el ion atómico padre se muestra con una línea vertical punteada que representa la interacción de Coulomb entre los electrones. El estado marcado con c describe la excitación del ion a un estado discreto o continuo. La figura b describe el proceso de intercambio. El modelo de Kuchiev, al contrario que el de Corkum, no predice ningún umbral de intensidad para la aparición de la ionización NS.
Kuciev no incluyó los efectos de Coulomb en la dinámica del electrón ionizado. Esto resultó en la subestimación de la tasa de doble ionización por un factor enorme. Obviamente, en el enfoque de Becker y Faisal (que es equivalente al modelo de Kuchiev en espíritu), este inconveniente no existe. De hecho, su modelo es más exacto y no sufre el gran número de aproximaciones realizadas por Kuchiev. Los resultados de sus cálculos se ajustan perfectamente a los resultados experimentales de Walker et al. Becker y Faisal han sido capaces de ajustar los resultados experimentales sobre el NSI múltiple de átomos de gases raros utilizando su modelo. Como resultado, la redistribución de electrones puede ser tomada como el principal mecanismo para la ocurrencia del proceso NSI.
Ionización multifotónica de electrones de valencia interna y fragmentación de moléculas poliatómicasEditar
La ionización de los electrones de valencia interna son responsables de la fragmentación de moléculas poliatómicas en campos láser fuertes. Según un modelo cualitativo la disociación de las moléculas se produce a través de un mecanismo de tres pasos:
- MPI de los electrones de los orbitales internos de la molécula que da lugar a un ion molecular en niveles ro-vibracionales de un estado electrónico excitado;
- Transición rápida sin radiación a los niveles ro-vibracionales de alto nivel de un estado electrónico inferior; y
- Siguiente disociación del ion a diferentes fragmentos a través de varios canales de fragmentación.







