Guinguette Marais Poitevin

Cómo manejar los eventos dependientes

¡La vida está llena de eventos aleatorios! Necesitas tener una «sensación» de ellos para ser una persona inteligente y exitosa.

Eventos Independientes

Los eventos pueden ser «Independientes», lo que significa que cada evento no se ve afectado por ningún otro evento.

Eventos Dependientes

Pero los eventos también pueden ser «dependientes»… lo que significa que pueden ser afectados por eventos anteriores…

Ejemplo: Canicas en una bolsa

En una bolsa hay 2 canicas azules y 3 rojas.

¿Cuál es la probabilidad de obtener una canica azul?

La probabilidad es de 2 entre 5

¡Pero después de sacar una las probabilidades cambian!

Así que la próxima vez:

si antes hemos sacado una canica roja, entonces la probabilidad de una canica azul a continuación es de 2 entre 4

si antes hemos sacado una canica azul, entonces la probabilidad de una canica azul a continuación es de 1 entre 4

Esto es porque estamos sacando canicas de la bolsa.

Así que el siguiente evento depende de lo que haya ocurrido en el evento anterior, y se llama dependiente.

Los eventos Dependientes son los que miramos aquí.

Diagrama de Árbol

Un Diagrama de Árbol: es una forma maravillosa de imaginar lo que está pasando, así que vamos a construir uno para nuestro ejemplo de las canicas.

Hay una probabilidad de 2/5 de sacar una canica Azul, y una probabilidad de 3/5 para la Roja:

Podemos ir un paso más allá y ver qué pasa cuando cogemos una segunda canica:

Si se seleccionó primero una canica azul ahora hay 1/4 de probabilidad de obtener una canica azul y 3/4 de obtener una canica roja.

Si se seleccionó primero una canica roja ahora hay una probabilidad de 2/4 de obtener una canica azul y una probabilidad de 2/4 de obtener una canica roja.

Notación

¡Nos encanta la notación en matemáticas! Significa que luego podemos usar el poder del álgebra para jugar con las ideas. Así que aquí está la notación para la probabilidad:

P(A) significa «Probabilidad del suceso A»

En nuestro ejemplo de las canicas el suceso A es «conseguir una canica azul primero» con una probabilidad de 2/5:

P(A) = 2/5

Y el suceso B es «conseguir una canica azul segundo»… pero para ello tenemos 2 opciones:

• Si conseguimos una Canica Azul primero la probabilidad es ahora de 1/4
• Si conseguimos una Canica Roja primero la probabilidad es ahora de 2/4

Así que tenemos que decir cuál queremos, y usar el símbolo «|» para significar «dado»:

P(B|A) significa «Evento B dado el evento A»

En otras palabras, el evento A ya ha ocurrido, ahora ¿cuál es la probabilidad del evento B?

P(B|A) también se llama la «Probabilidad Condicional» de B dado A.

Y en nuestro caso:

P(B|A) = 1/4

Así que la probabilidad de obtener 2 canicas azules es:



Y lo escribimos como



.

«Probabilidad del suceso A y del suceso B es igual a
la probabilidad del suceso A por la probabilidad del suceso B dado el suceso A»

Hagamos el siguiente ejemplo utilizando sólo la notación:

Ejemplo: Sacar 2 reyes de una baraja

El suceso A es sacar un rey primero, y el suceso B es sacar un rey después.

Para la primera carta la probabilidad de sacar un Rey es 4 de 52 (hay 4 Reyes en una baraja de 52 cartas):

P(A) = 4/52

Pero después de quitar un Rey de la baraja la probabilidad de que la 2ª carta sacada sea menos probable que sea un Rey (sólo 3 de las 51 cartas que quedan son Reyes):

P(B|A) = 3/51

Y así:

P(A y B) = P(A) x P(B|A) =(4/52)x (3/51) = 12/2652 = 1/221

Así que la probabilidad de obtener 2 Reyes es de 1 entre 221, o sea, aproximadamente el 0.5%

Buscando datos ocultos

Utilizando el Álgebra también podemos «cambiar el tema» de la fórmula, así:

Empezar por:	P(A y B) = P(A) x P(B|A)
Intercambiar los lados:		P(A) x P(B|A) = P(A y B)	Dividir por P(A):		P(B|A) = P(A y B) / P(A)

Y tenemos otra fórmula útil:



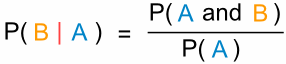
«La probabilidad del suceso B dado el suceso A es igual a
la probabilidad del suceso A y del suceso B dividida por la probabilidad del suceso A

Ejemplo: Helados

Al 70% de tus amigos les gusta el Chocolate, y al 35% les gusta el Chocolate Y les gusta la Fresa.

¿Qué porcentaje de los que les gusta el Chocolate también les gusta la Fresa?

P(Fresa|Chocolate) = P(Chocolate y Fresa) / P(Chocolate)

0,35 / 0.7 = 50%

El 50% de tus amigos a los que les gusta el Chocolate también les gusta la Fresa



Gran ejemplo: Partido de fútbol

Te vas al fútbol, y quieres ser el Portero, pero eso depende de quién sea el Entrenador hoy:

• con el Entrenador Sam la probabilidad de ser Portero es 0,5
• con el Entrenador Alex la probabilidad de ser Portero es 0.3

Sam es Entrenador más a menudo… unos 6 de cada 10 partidos (una probabilidad de 0,6).

Entonces, ¿cuál es la probabilidad de que seas Portero hoy?

Construyamos un diagrama de árbol. Primero mostramos los dos posibles entrenadores: Sam o Alex:



La probabilidad de que te toque Sam es de 0,6, por lo que la de Alex debe ser de 0,4 (juntas la probabilidad es de 1)

Ahora, si te toca Sam, hay 0,5 de probabilidad de ser Portero (y 0.5 de no ser Portero):



Si te toca Alex, hay 0,3 de probabilidad de ser Portero (y 0.7 no):



El diagrama de árbol está completo, ahora vamos a calcular las probabilidades globales. Recuerda que:

P(A y B) = P(A) x P(B|A)

Aquí tienes cómo hacerlo para la rama «Sam, Sí»:



(Cuando tomamos la 0.6 de probabilidad de que Sam sea entrenador por el 0,5 de probabilidad de que Sam le deje ser portero terminamos con un 0,3 de probabilidad.)

¡Pero aún no hemos terminado! No hemos incluido a Alex como Entrenador:



Una probabilidad de 0,4 de que Alex sea Entrenador, seguida de una probabilidad de 0,3 da 0,12

Y las dos ramas «Sí» del árbol juntas hacen:

0,3 + 0,12 = 0.42 de probabilidad de ser portero hoy

(Es decir, un 42% de probabilidad)

Comprobar

Un último paso: completar los cálculos y asegurarse de que suman 1:



0.3 + 0,3 + 0,12 + 0,28 = 1

Sí, suman 1, así que parece correcto.

Amigos y números aleatorios

Aquí tenemos otro ejemplo bastante diferente de Probabilidad Condicional.

4 amigos (Alex, Blake, Chris y Dusty) eligen cada uno un número aleatorio entre 1 y 5. Cuál es la probabilidad de que alguno de ellos haya elegido el mismo número?

Sumemos a nuestros amigos de uno en uno…

Primero, ¿cuál es la probabilidad de que Alex y Blake tengan el mismo número?

Blake compara su número con el de Alex. Hay una probabilidad de 1 entre 5 de que coincidan.

Como diagrama de árbol:



Nota: «Sí» y «No» juntos hacen 1
(1/5 + 4/5 = 5/5 = 1)

Ahora, incluyamos a Chris…

Pero ahora hay dos casos a considerar:

• Si Alex y Blake coincidieron, entonces Chris sólo tiene un número para comparar.
• Pero si Alex y Blake no coincidieron entonces Chris tiene dos números para comparar.

Y obtenemos esto:



Para la línea superior (Alex y Blake coincidieron) ya tenemos una coincidencia (una probabilidad de 1/5).

Pero para la línea «Alex y Blake no coincidieron» ahora hay una probabilidad de 2/5 de que Chris coincida (porque Chris consigue igualar su número tanto con Alex como con Blake).

Y podemos calcular la probabilidad combinada multiplicando las probabilidades que se necesitaron para llegar allí:

Siguiendo el camino «No, Sí» … hay una probabilidad de 4/5 de No, seguida de una probabilidad de 2/5 de Sí:

(4/5) × (2/5) = 8/25

Siguiendo el camino «No, No» … hay una probabilidad de 4/5 de No, seguida de una probabilidad de 3/5 de No:

(4/5) × (3/5) = 12/25

También fíjate en que cuando sumamos todas las probabilidades seguimos obteniendo 1 (una buena comprobación de que no nos hemos equivocado):

(5/25) + (8/25) + (12/25) = 25/25 = 1

¿Ahora qué pasa cuando incluimos a Dusty?

Es la misma idea, sólo que más de ella:



Ok, son los 4 amigos, y las posibilidades de «Sí» juntas hacen 101/125:

Respuesta: 101/125

Pero aquí hay algo interesante… si seguimos el camino del «No» podemos saltarnos todos los demás cálculos y hacernos la vida más fácil:



Las probabilidades de no coincidir son:

(4/5) × (3/5) × (2/5) = 24/125

Así que las probabilidades de coincidir son:

1 – (24/125) = 101/125

(¡Y realmente no necesitábamos un diagrama de árbol para eso!)