Contenidos:
- ¿Qué es una prueba T?
- La puntuación T
- Valores T y valores P
- Cálculo de la prueba T
- ¿Qué es una prueba T emparejada (prueba T de muestras emparejadas)?
- Una puntuación t grande le indica que los grupos son diferentes.
- Una puntuación t pequeña le indica que los grupos son similares.
- Una prueba t de muestras independientes compara las medias de dos grupos.
- Una prueba t de muestras pareadas compara las medias del mismo grupo en diferentes momentos (digamos, con un año de diferencia).
- Una prueba t de una muestra compara la media de un solo grupo con una media conocida.
- Los costes de la resonancia magnética de la rodilla en dos hospitales diferentes,
- Dos pruebas en la misma persona antes y después del entrenamiento,
- Dos mediciones de la presión arterial en la misma persona utilizando equipos diferentes.
- ΣD: Suma de las diferencias (Suma de X-Y del paso 2)
- ΣD2: Suma de las diferencias al cuadrado (del paso 4)
- (ΣD)2: Suma de las diferencias (del paso 2), al cuadrado.
¿Qué es una prueba T?
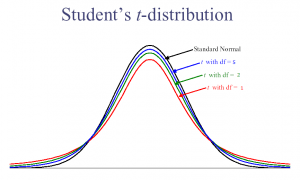
Varios grados de libertad para la T de Student.
Un ejemplo muy sencillo: Digamos que tienes un resfriado y pruebas un remedio naturista. Tu resfriado dura un par de días. La siguiente vez que tienes un resfriado, compras un medicamento de venta libre y el resfriado te dura una semana. Haces una encuesta entre tus amigos y todos te dicen que sus resfriados duraron menos (una media de 3 días) cuando tomaron el remedio homeopático. Lo que realmente quieres saber es si estos resultados son repetibles. Una prueba t puede decírselo comparando las medias de los dos grupos y permitiéndole conocer la probabilidad de que esos resultados se produzcan por azar.
Otro ejemplo: Las pruebas T de Student pueden utilizarse en la vida real para comparar medias. Por ejemplo, una empresa farmacéutica puede querer probar un nuevo medicamento contra el cáncer para averiguar si mejora la esperanza de vida. En un experimento, siempre hay un grupo de control (un grupo al que se le da un placebo, o «píldora de azúcar»). El grupo de control puede mostrar una esperanza de vida media de +5 años, mientras que el grupo que toma el nuevo fármaco podría tener una esperanza de vida de +6 años. Parecería que el fármaco podría funcionar. Pero podría deberse a una casualidad. Para comprobarlo, los investigadores utilizarían una prueba t de Student para averiguar si los resultados son repetibles para toda una población.
¿Todavía tienes problemas? Chegg.com te pondrá en contacto con un tutor virtual (¡y tus primeros 30 minutos son gratis!).
La puntuación T.
La puntuación t es un cociente entre la diferencia entre dos grupos y la diferencia dentro de los grupos. Cuanto mayor sea la puntuación t, más diferencia hay entre los grupos. Cuanto más pequeña sea la puntuación t, mayor será la similitud entre los grupos. Una puntuación t de 3 significa que los grupos son tres veces más diferentes entre sí que dentro de ellos. Cuando se realiza una prueba t, cuanto mayor sea el valor t, más probable es que los resultados sean repetibles.
Valores t y valores p
¿Cómo de grande es «lo suficientemente grande»? Cada valor t tiene un valor p que lo acompaña. Un valor p es la probabilidad de que los resultados de los datos de la muestra se hayan producido por casualidad. Los valores p van del 0% al 100%. Suelen escribirse con un decimal. Por ejemplo, un valor p del 5% es 0,05. Los valores p bajos son buenos; indican que los datos no se produjeron por casualidad. Por ejemplo, un valor p de 0,01 significa que sólo hay un 1% de probabilidad de que los resultados de un experimento se hayan producido por casualidad. En la mayoría de los casos, un valor p de 0,05 (5%) se acepta para significar que los datos son válidos.
Cálculo del estadístico / Tipos de prueba
Hay tres tipos principales de prueba t:
Probablemente no quiera calcular la prueba a mano (las matemáticas pueden ser muy complicadas, pero si insiste puede encontrar los pasos para una prueba t de muestras independientes aquí.
Usa las siguientes herramientas para calcular la prueba t:
Cómo hacer una prueba T en Excel.
Prueba T en SPSS.
Distribución T en la TI 89.
Distribución T en la TI 83.
¿Qué es una prueba T emparejada (prueba T de muestras emparejadas / prueba T de muestras dependientes)?
Una prueba t emparejada (también llamada prueba t de pares correlacionados, prueba t de muestras emparejadas o prueba t de muestras dependientes) consiste en realizar una prueba t sobre muestras dependientes. Las muestras dependientes están esencialmente conectadas: son pruebas sobre la misma persona o cosa. Por ejemplo:
Cuándo elegir una prueba T emparejada / Prueba T de muestras emparejadas / Prueba T de muestras dependientes
Elija la prueba t emparejada si tiene dos mediciones sobre el mismo elemento, persona o cosa. También debe elegir esta prueba si tiene dos artículos que se están midiendo con una condición única. Por ejemplo, podría estar midiendo el rendimiento de la seguridad de los coches en Investigación y Pruebas de Vehículos y someter los coches a una serie de pruebas de choque. Aunque los fabricantes son diferentes, podría estar sometiéndolos a las mismas condiciones.
Con una prueba t de dos muestras «normal», está comparando las medias de dos muestras diferentes. Por ejemplo, podría probar dos grupos diferentes de asociados de servicio al cliente en una prueba relacionada con el negocio o probar a los estudiantes de dos universidades en sus habilidades de inglés. Si toma una muestra aleatoria de cada grupo por separado y tienen condiciones diferentes, sus muestras son independientes y debe ejecutar una prueba t de muestras independientes (también llamada entre muestras y muestras no apareadas).
La hipótesis nula para la prueba t de muestras independientes es μ1 = μ2. En otras palabras, asume que las medias son iguales. Con la prueba t pareada, la hipótesis nula es que la diferencia por pares entre las dos pruebas es igual (H0: µd = 0). La diferencia entre las dos pruebas es muy sutil; la que elija se basa en su método de recogida de datos.
Prueba T de muestras pareadas a mano
Pregunta de ejemplo: Calcule una prueba t emparejada a mano para los siguientes datos: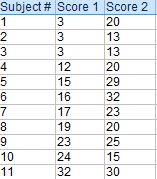
Paso 1: reste cada puntuación Y de cada puntuación X.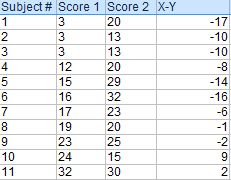
Paso 2: sume todos los valores del paso 1.
Aparte este número por un momento.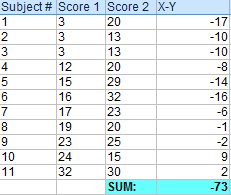
Paso 3: Eleve al cuadrado las diferencias del Paso 1.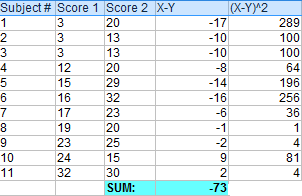
Paso 4: Sume todas las diferencias elevadas al cuadrado del Paso 3.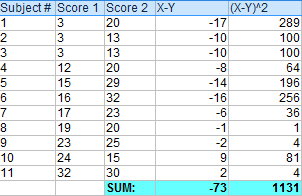
Paso 5: Utilice la siguiente fórmula para calcular la puntuación t: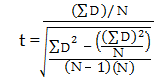
Si no está familiarizado con Σ es posible que quiera leer primero sobre la notación de la suma.
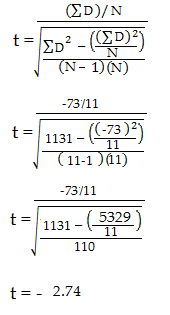
Paso 6: Reste 1 del tamaño de la muestra para obtener los grados de libertad. Tenemos 11 elementos, por lo que 11-1 = 10.
Paso 7: Encuentre el valor p en la tabla t, utilizando los grados de libertad del paso 6. Si no tiene un nivel alfa especificado, utilice 0,05 (5%). Para este problema de ejemplo, con df = 10, el valor t es 2,228.
Paso 8: Compare su valor de la tabla t del Paso 7 (2,228) con su valor t calculado (-2,74). El valor t calculado es mayor que el valor de la tabla a un nivel alfa de 0,05. El valor p es menor que el nivel alfa: p <.05. Podemos rechazar la hipótesis nula de que no hay diferencia entre las medias.
Nota: Puede ignorar el signo menos al comparar los dos valores t, ya que ± indica la dirección; el valor p sigue siendo el mismo para ambas direcciones.
¡Consulte nuestro canal de YouTube para obtener más ayuda y consejos sobre estadísticas!
Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp. 50-55, 1956.
Stephanie Glen. «T Test (Student’s T-Test): Definición y ejemplos» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/probability-and-statistics/t-test/
——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!