
La regresión logística se utilizó en las ciencias biológicas a principios del siglo XX. Después se utilizó en muchas aplicaciones de las ciencias sociales. La regresión logística se utiliza cuando la variable dependiente (objetivo) es categórica.
Por ejemplo,
- Predecir si un correo electrónico es spam (1) o (0)
- Si el tumor es maligno (1) o no (0)
Considere un escenario en el que necesitamos clasificar si un correo electrónico es spam o no. Si utilizamos la regresión lineal para este problema, es necesario establecer un umbral en base al cual se puede hacer la clasificación. Digamos que si la clase real es maligna, el valor continuo predicho es 0,4 y el valor del umbral es 0,5, el punto de datos se clasificará como no maligno, lo que puede llevar a una consecuencia grave en tiempo real.
De este ejemplo, se puede deducir que la regresión lineal no es adecuada para el problema de clasificación. La regresión lineal no tiene límites, y esto hace que la regresión logística entre en escena. Su valor oscila estrictamente entre 0 y 1.
Regresión logística simple
(Código fuente completo: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Modelo
Salida = 0 o 1
Hipótesis => Z = WX + B
hΘ(x) = sigmoide (Z)
Sigmoide Función

Si ‘Z’ llega al infinito, Y(predicted) se convertirá en 1 y si ‘Z’ llega al infinito negativo, Y(predicted) se convertirá en 0.
Análisis de la hipótesis
La salida de la hipótesis es la probabilidad estimada. Esto se utiliza para inferir cómo de seguro puede ser el valor predicho el valor real cuando se da una entrada X. Considere el siguiente ejemplo,
X = =
Basado en el valor x1, digamos que obtuvimos la probabilidad estimada para ser 0,8. Esto nos dice que hay un 80% de posibilidades de que un correo electrónico sea spam.
Matemáticamente esto se puede escribir como,

Esto justifica el nombre de «regresión logística». Los datos se ajustan a un modelo de regresión lineal, sobre el que luego actúa una función logística que predice la variable dependiente categórica objetivo.
Tipos de regresión logística
1. Regresión logística binaria
La respuesta categórica tiene sólo dos 2 resultados posibles. Ejemplo: Spam o No
2. Regresión Logística Multinomial
Tres o más categorías sin ordenar. Ejemplo: Predecir qué comida se prefiere más (Veg, No-Veg, Vegano)
3. Regresión Logística Ordinal
Tres o más categorías con ordenación. Ejemplo: Valoración de películas del 1 al 5
Límite de decisión
Para predecir a qué clase pertenece un dato, se puede establecer un umbral. En base a este umbral, la probabilidad estimada obtenida se clasifica en clases.
Por ejemplo, si valor_previsto ≥ 0,5, entonces clasifica el correo electrónico como spam, si no, como no spam.
El límite de decisión puede ser lineal o no lineal. Se puede aumentar el orden polinómico para obtener un límite de decisión complejo.
Función de coste
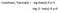
¿Por qué la función de coste que se ha utilizado para la lineal no se puede utilizar para la logística?
La regresión lineal utiliza el error medio cuadrático como función de coste. Si se utiliza para la regresión logística, entonces será una función no convexa de los parámetros (theta). El descenso gradual convergerá al mínimo global sólo si la función es convexa.

Explicación de la función de coste


Función de coste simplificada

¿Por qué esta función de costes?
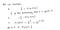
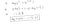
Esta función negativa se debe a que cuando entrenamos, necesitamos maximizar la probabilidad minimizando la función de pérdida. Disminuir el coste aumentará la máxima probabilidad asumiendo que las muestras se extraen de una distribución idénticamente independiente.
Derivando la fórmula del Algoritmo de Ascenso Gradiente


Implementación en Python
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Coste vs Número_de_Iteraciones

La precisión de entrenamiento y prueba del sistema es del 100 %
Esta implementación es para regresión logística binaria. Para datos con más de 2 clases, hay que utilizar la regresión softmax.
Este es un post educativo e inspirado en el curso de aprendizaje profundo del profesor Andrew Ng.
Código completo : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb