Guinguette Marais Poitevin

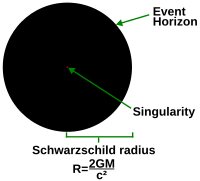
Las soluciones a las ecuaciones de la relatividad general u otra teoría de la gravedad (como la supergravedad) suelen dar lugar a encontrar puntos en los que la métrica estalla hasta el infinito. Sin embargo, muchos de estos puntos son completamente regulares, y los infinitos son simplemente el resultado de utilizar un sistema de coordenadas inapropiado en este punto. Para comprobar si hay una singularidad en un punto determinado, hay que comprobar si en ese punto las cantidades invariantes del difeomorfismo (es decir, los escalares) se vuelven infinitas. Dichas cantidades son las mismas en todos los sistemas de coordenadas, por lo que estos infinitos no «desaparecerán» por un cambio de coordenadas.

Un ejemplo es la solución de Schwarzschild que describe un agujero negro sin carga y sin rotación. En los sistemas de coordenadas convenientes para trabajar en regiones alejadas del agujero negro, una parte de la métrica se vuelve infinita en el horizonte de sucesos. Sin embargo, el espaciotiempo en el horizonte de sucesos es regular. La regularidad se hace evidente al cambiar a otro sistema de coordenadas (como las coordenadas de Kruskal), donde la métrica es perfectamente suave. Por otro lado, en el centro del agujero negro, donde la métrica también se vuelve infinita, las soluciones sugieren que existe una singularidad. La existencia de la singularidad puede verificarse observando que el escalar de Kretschmann, siendo el cuadrado del tensor de Riemann, es decir, R μ ν ρ σ R μ ν ρ σ {\displaystyle R_{mu \nu \rho \sigma }R^{mu \nu \rho \sigma }}.

, que es invariante del difeomorfismo, es infinito.

Mientras que en un agujero negro no giratorio la singularidad se produce en un único punto de las coordenadas del modelo, llamado «singularidad puntual», en un agujero negro giratorio, también conocido como agujero negro de Kerr, la singularidad se produce en un anillo (una línea circular), conocido como «singularidad anular». Dicha singularidad también puede convertirse teóricamente en un agujero de gusano.

De forma más general, un espaciotiempo se considera singular si es geodésicamente incompleto, lo que significa que hay partículas en caída libre cuyo movimiento no puede determinarse más allá de un tiempo finito, siendo posterior al punto de alcanzar la singularidad. Por ejemplo, cualquier observador dentro del horizonte de sucesos de un agujero negro no giratorio caería en su centro en un periodo de tiempo finito. La versión clásica del modelo cosmológico del universo del Big Bang contiene una singularidad causal al comienzo del tiempo (t=0), donde todas las geodésicas temporales no tienen extensiones hacia el pasado. Si se extrapola hacia atrás hasta este hipotético tiempo 0, se obtiene un universo con todas las dimensiones espaciales de tamaño cero, densidad infinita, temperatura infinita y curvatura infinita del espaciotiempo.

Singularidad desnudaEditar

Hasta principios de la década de 1990, estaba muy extendida la creencia de que la relatividad general oculta todas las singularidades detrás de un horizonte de sucesos, lo que hace imposible las singularidades desnudas. Esto se conoce como la hipótesis de la censura cósmica. Sin embargo, en 1991, los físicos Stuart Shapiro y Saul Teukolsky realizaron simulaciones por ordenador de un plano de polvo en rotación que indicaban que la relatividad general podría permitir singularidades «desnudas». Se desconoce el aspecto que tendrían estos objetos en un modelo de este tipo. Tampoco se sabe si las singularidades seguirían apareciendo si se eliminaran las suposiciones simplificadoras utilizadas para hacer la simulación. Sin embargo, se plantea la hipótesis de que la luz que entra en una singularidad tendría igualmente sus geodésicas terminadas, con lo que la singularidad desnuda se parecería a un agujero negro.

Los horizontes de sucesos que desaparecen existen en la métrica de Kerr, que es un agujero negro que gira en el vacío, si el momento angular ( J {\displaystyle J}

) es lo suficientemente alto. Transformando la métrica de Kerr a coordenadas de Boyer-Lindquist, se puede demostrar que la coordenada (que no es el radio) del horizonte de sucesos es, r ± = μ ± ( μ 2 – a 2 ) 1 / 2 {\displaystyle r_{{pm }=\mu \pm (\mu ^{2}-a^{2})^{1/2}

, donde μ = G M / c 2 {\displaystyle \mu =GM/c^{2}}

, y a = J / M c {\displaystyle a=J/Mc}

. En este caso, «los horizontes de sucesos desaparecen» significa cuando las soluciones son complejas para r ± {\displaystyle r_{\pm }}

, o μ 2 < a 2 {\displaystyle \mu ^{2}<a^{2}.

. Sin embargo, esto corresponde a un caso en el que J {\displaystyle J}

supera a G M 2 / c {\displaystyle GM^{2}/c}

(o en unidades Planck, J > M 2 {{displaystyle J>M^{2}}

), es decir, el espín supera lo que normalmente se considera el límite superior de sus valores físicamente posibles.

De forma similar, también se pueden observar horizontes de sucesos que desaparecen con la geometría de Reissner-Nordström de un agujero negro cargado si la carga ( Q {\displaystyle Q}

) es lo suficientemente alta. En esta métrica, puede demostrarse que las singularidades se producen en r ± = μ ± ( μ 2 – q 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-q^{2})^{1/2}

, donde μ = G M / c 2 {\displaystyle \mu =GM/c^{2}}

, y q 2 = G Q 2 / ( 4 π ϵ 0 c 4 ) {\displaystyle q^{2}=GQ^{2}/(4\pi \silon _{0}c^{4})}

. De los tres casos posibles para los valores relativos de μ {\displaystyle \mu }

y q {\displaystyle q}

, el caso en que μ 2 < q 2 {\displaystyle \mu ^{2}<q^{2}

causa tanto r ± {\displaystyle r_{\pm }}

sean complejos. Esto significa que la métrica es regular para todos los valores positivos de r {\displaystyle r}

, o en otras palabras, la singularidad no tiene horizonte de sucesos. Sin embargo, esto corresponde a un caso en el que Q / 4 π ϵ 0 {\displaystyle Q/{sqrt {4\pi \epsilon _{0}}}}

supera a M G {{displaystyle M{{sqrt {G}}

(o en unidades Planck, Q > M {{displaystyle Q>M}

), es decir, la carga supera lo que normalmente se considera el límite superior de sus valores físicamente posibles. Además, no se espera que los agujeros negros astrofísicos reales posean ninguna carga apreciable.

Un agujero negro que posea la menor M

valor consistente con su J {\displaystyle J}

y Q {\displaystyle Q}

y los límites señalados anteriormente, es decir, uno justo en el punto de perder su horizonte de sucesos, se denomina extremo.