Tal vez se pregunte de qué se tratan todas esas sumas de cuadrados. Tal vez eso es lo que te trajo aquí en primer lugar. Pues bien, son los determinantes de una buena regresión lineal. Este tutorial se basa en el marco de ANOVA que puede haber escuchado antes.
Antes de leerlo, sin embargo, asegúrese de que no está confundiendo la regresión con la correlación. Si tienes esto comprobado, podemos pasar directamente a la acción.
Una rápida nota al margen: ¿Quieres aprender más sobre la regresión lineal? Echa un vistazo a nuestros vídeos explicativos El modelo de regresión lineal. Representación geométrica y El modelo de regresión lineal simple.
SST, SSR, SSE: Definición y fórmulas
Hay tres términos que debemos definir. La suma de los cuadrados totales, la suma de la regresión de los cuadrados y la suma del error de los cuadrados.

¿Qué es la SST?
La suma de los cuadrados totales, denotada SST, es la diferencia al cuadrado entre la variable dependiente observada y su media. Puede pensar en esto como la dispersión de las variables observadas en torno a la media – muy parecido a la varianza en la estadística descriptiva.
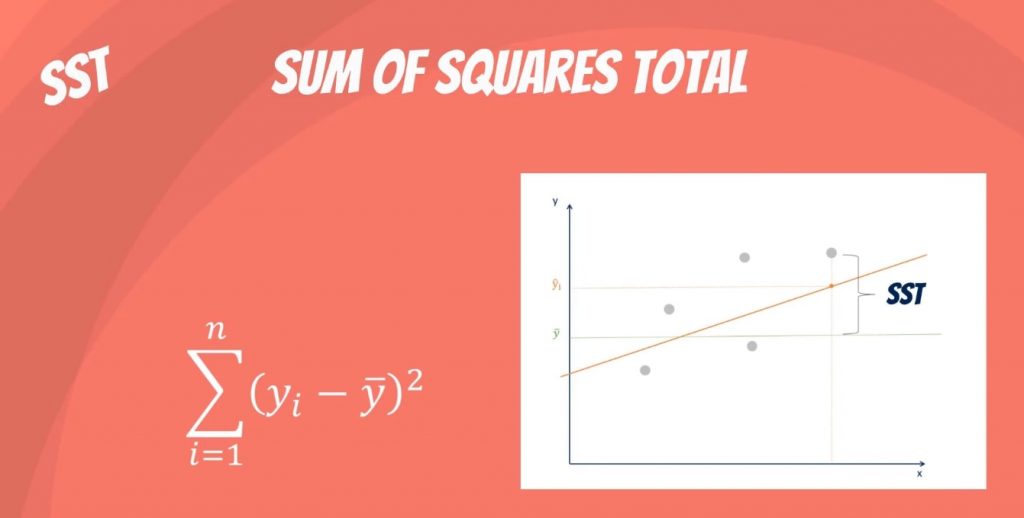
Es una medida de la variabilidad total del conjunto de datos.
Nota al margen: Hay otra notación para la SST. Es TSS o suma total de cuadrados.
¿Qué es el SSR?
El segundo término es la suma de cuadrados debida a la regresión, o SSR. Es la suma de las diferencias entre el valor predicho y la media de la variable dependiente. Piense en ello como una medida que describe lo bien que nuestra recta se ajusta a los datos.

Si este valor de SSR es igual a la suma de cuadrados total, significa que nuestro modelo de regresión captura toda la variabilidad observada y es perfecto. Una vez más, tenemos que mencionar que otra notación común es ESS o suma de cuadrados explicada.
¿Qué es el SSE?
El último término es el error de la suma de cuadrados, o SSE. El error es la diferencia entre el valor observado y el valor predicho.

Normalmente queremos minimizar el error. Cuanto menor sea el error, mejor será el poder de estimación de la regresión. Por último, debo añadir que también se conoce como RSS o suma de cuadrados residual. Residual como: restante o inexplicable.
La confusión entre las diferentes abreviaturas
Se hace realmente confuso porque algunos lo denotan como SSR. Esto hace que no quede claro si estamos hablando de la suma de cuadrados debida a la regresión o de la suma de residuos al cuadrado.

En cualquier caso, ninguna de las dos está adoptada universalmente, así que la confusión se mantiene y tendremos que vivir con ella.
Sólo hay que recordar que las dos notaciones son SST, SSR, SSE, o TSS, ESS, RSS.

Hay un conflicto en cuanto a las abreviaturas, pero no en cuanto al concepto y su aplicación. Así que vamos a centrarnos en eso.
¿Cómo se relacionan?
Matemáticamente, TSE = SSR + SSE.

El razonamiento es el siguiente: la variabilidad total del conjunto de datos es igual a la variabilidad explicada por la recta de regresión más la variabilidad no explicada, conocida como error.

Dada una variabilidad total constante, un error menor causará una mejor regresión. Por el contrario, un error más alto provocará una regresión menos potente. Y eso es lo que debes recordar, sin importar la notación.
Siguiente paso: La R-cuadrada
Bueno, si no estás seguro de por qué necesitamos todas esas sumas de cuadrados, tenemos justo la herramienta adecuada para ti. El R-cuadrado. ¿Quieres saber más? Sólo tienes que sumergirte en el tutorial enlazado donde entenderás cómo mide el poder explicativo de una regresión lineal!
***
¿Interesado en aprender más? Puedes llevar tus habilidades de buenas a grandes con nuestro curso de estadística.
Prueba el curso de estadística gratis
Siguiente tutorial: Midiendo la variabilidad con la R-cuadrada