Dans ce tutoriel, nous allons présenter une structure de compensateur de rétroaction simple, mais polyvalente : le contrôleur proportionnel-intégral-dérivé (PID). Le contrôleur PID est largement employé parce qu’il est très compréhensible et parce qu’il est assez efficace. L’un des attraits du contrôleur PID est que tous les ingénieurs comprennent les concepts de différenciation et d’intégration, ce qui leur permet de mettre en œuvre le système de contrôle même sans avoir une connaissance approfondie de la théorie du contrôle. De plus, même si le compensateur est simple, il est assez sophistiqué dans la mesure où il saisit l’historique du système (par intégration) et anticipe le comportement futur du système (par différenciation). Nous discuterons de l’effet de chacun des paramètres PID sur la dynamique d’un système en boucle fermée et nous démontrerons comment utiliser un contrôleur PID pour améliorer les performances d’un système.
Les commandes MATLAB clés utilisées dans ce tutoriel sont : tf , step , pid , feedback , pidtune
PID Overview
Dans ce tutoriel, nous allons considérer le système à rétroaction unitaire suivant :
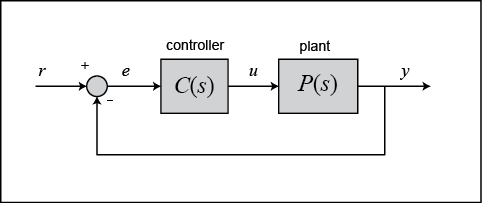
La sortie d’un contrôleur PID, qui est égale à l’entrée de commande de la plante, est calculée dans le domaine temporel à partir de l’erreur de rétroaction comme suit :
(1)
D’abord, voyons comment le contrôleur PID fonctionne dans un système en boucle fermée à l’aide du schéma présenté ci-dessus. La variable ( ) représente l’erreur de suivi, la différence entre la sortie souhaitée (
) représente l’erreur de suivi, la différence entre la sortie souhaitée ( ) et la sortie réelle (
) et la sortie réelle ( ). Ce signal d’erreur (
). Ce signal d’erreur ( ) est envoyé au contrôleur PID, et le contrôleur calcule à la fois la dérivée et l’intégrale de ce signal d’erreur par rapport au temps. Le signal de commande (
) est envoyé au contrôleur PID, et le contrôleur calcule à la fois la dérivée et l’intégrale de ce signal d’erreur par rapport au temps. Le signal de commande ( ) à la plante est égal au gain proportionnel (
) à la plante est égal au gain proportionnel ( ) multiplié par l’amplitude de l’erreur plus le gain intégral (
) multiplié par l’amplitude de l’erreur plus le gain intégral ( ) fois l’intégrale de l’erreur plus le gain dérivé (
) fois l’intégrale de l’erreur plus le gain dérivé ( ) fois la dérivée de l’erreur.
) fois la dérivée de l’erreur.
Ce signal de commande ( ) est envoyé à la centrale et la nouvelle sortie (
) est envoyé à la centrale et la nouvelle sortie ( ) est obtenue. La nouvelle sortie (
) est obtenue. La nouvelle sortie ( ) est ensuite réinjectée et comparée à la référence pour trouver le nouveau signal d’erreur (
) est ensuite réinjectée et comparée à la référence pour trouver le nouveau signal d’erreur ( ). Le contrôleur prend ce nouveau signal d’erreur et calcule une mise à jour de l’entrée de commande. Ce processus se poursuit tant que le contrôleur est en vigueur.
). Le contrôleur prend ce nouveau signal d’erreur et calcule une mise à jour de l’entrée de commande. Ce processus se poursuit tant que le contrôleur est en vigueur.
La fonction de transfert d’un contrôleur PID est trouvée en prenant la transformée de Laplace de l’équation (1).
(2)
où  = gain proportionnel,
= gain proportionnel,  = gain intégral, et
= gain intégral, et  = gain dérivé.
= gain dérivé.
Nous pouvons définir un contrôleur PID dans MATLAB en utilisant directement un modèle de fonction de transfert, par exemple :
Kp = 1;Ki = 1;Kd = 1;s = tf('s');C = Kp + Ki/s + Kd*s
C = s^2 + s + 1 ----------- s Continuous-time transfer function.
Alternativement, nous pouvons utiliser l’objet pid de MATLAB pour générer un contrôleur à temps continu équivalent comme suit :
C = pid(Kp,Ki,Kd)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.
Convertissons l’objet pid en fonction de transfert pour vérifier qu’il donne le même résultat que ci-dessus :
tf(C)
ans = s^2 + s + 1 ----------- s Continuous-time transfer function.
Les caractéristiques des termes P, I et D
L’augmentation du gain proportionnel ( ) a pour effet d’augmenter proportionnellement le signal de commande pour un même niveau d’erreur. Le fait que le contrôleur « pousse » plus fort pour un niveau d’erreur donné tend à faire réagir le système en boucle fermée plus rapidement, mais aussi à le faire dépasser davantage. Un autre effet de l’augmentation de
) a pour effet d’augmenter proportionnellement le signal de commande pour un même niveau d’erreur. Le fait que le contrôleur « pousse » plus fort pour un niveau d’erreur donné tend à faire réagir le système en boucle fermée plus rapidement, mais aussi à le faire dépasser davantage. Un autre effet de l’augmentation de  est qu’elle tend à réduire, mais pas à éliminer, l’erreur en régime permanent.
est qu’elle tend à réduire, mais pas à éliminer, l’erreur en régime permanent.
L’ajout d’un terme dérivé au contrôleur ( ) ajoute la capacité du contrôleur à » anticiper » l’erreur. Avec une commande proportionnelle simple, si
) ajoute la capacité du contrôleur à » anticiper » l’erreur. Avec une commande proportionnelle simple, si  est fixe, la seule façon dont la commande augmentera est si l’erreur augmente. Avec la commande dérivée, le signal de commande peut devenir important si l’erreur commence à suivre une pente ascendante, même si l’ampleur de l’erreur est encore relativement faible. Cette anticipation tend à ajouter de l’amortissement au système, diminuant ainsi le dépassement. L’ajout d’un terme dérivé, cependant, n’a aucun effet sur l’erreur en régime permanent.
est fixe, la seule façon dont la commande augmentera est si l’erreur augmente. Avec la commande dérivée, le signal de commande peut devenir important si l’erreur commence à suivre une pente ascendante, même si l’ampleur de l’erreur est encore relativement faible. Cette anticipation tend à ajouter de l’amortissement au système, diminuant ainsi le dépassement. L’ajout d’un terme dérivé, cependant, n’a aucun effet sur l’erreur en régime permanent.
L’ajout d’un terme intégral au contrôleur ( ) tend à aider à réduire l’erreur en régime permanent. En cas d’erreur persistante et régulière, l’intégrateur s’accumule et s’accumule, ce qui augmente le signal de commande et fait baisser l’erreur. Un inconvénient du terme intégral, cependant, est qu’il peut rendre le système plus lent (et oscillatoire), car lorsque le signal d’erreur change de signe, l’intégrateur peut mettre un certain temps à se « dérouler ».
) tend à aider à réduire l’erreur en régime permanent. En cas d’erreur persistante et régulière, l’intégrateur s’accumule et s’accumule, ce qui augmente le signal de commande et fait baisser l’erreur. Un inconvénient du terme intégral, cependant, est qu’il peut rendre le système plus lent (et oscillatoire), car lorsque le signal d’erreur change de signe, l’intégrateur peut mettre un certain temps à se « dérouler ».
Les effets généraux de chaque paramètre du contrôleur (

 ) sur un système en boucle fermée sont résumés dans le tableau ci-dessous. Notez que ces directives sont valables dans de nombreux cas, mais pas dans tous. Si vous voulez vraiment connaître l’effet du réglage des gains individuels, vous devrez faire plus d’analyse, ou devrez effectuer des tests sur le système réel.
) sur un système en boucle fermée sont résumés dans le tableau ci-dessous. Notez que ces directives sont valables dans de nombreux cas, mais pas dans tous. Si vous voulez vraiment connaître l’effet du réglage des gains individuels, vous devrez faire plus d’analyse, ou devrez effectuer des tests sur le système réel.
| |
|
|||
| |
Exemple de problème
Supposons que nous ayons un système simple de masse-.ressort-amortisseur.

L’équation directrice de ce système est
(3)
En prenant la transformée de Laplace de l’équation directrice, nous obtenons
(4)
La fonction de transfert entre la force d’entrée  et le déplacement de sortie
et le déplacement de sortie  devient alors
devient alors
(5)
Laissons
m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N
Substituer ces valeurs dans la fonction de transfert ci-dessus
(6)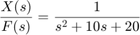
Le but de ce problème est de montrer comment chacun des termes, 
 , et
, et  , contribue à l’obtention des objectifs communs de :
, contribue à l’obtention des objectifs communs de :
- Temps de montée rapide
- Surpassement minimal
- Erreur en régime permanent nulle
Réponse en échelon en boucle ouverte
Voyons d’abord la réponse en échelon en boucle ouverte. Créez un nouveau fichier m et exécutez le code suivant :
s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)
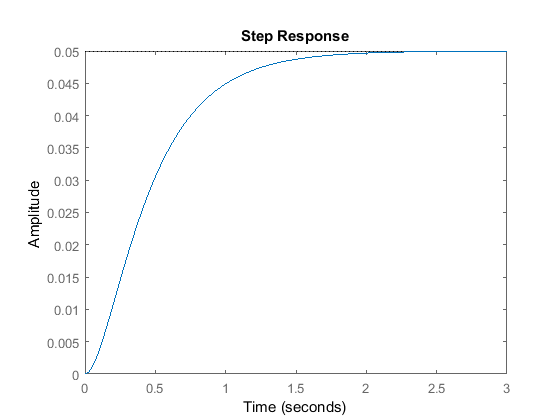
Le gain en courant continu de la fonction de transfert de l’usine est de 1/20, donc 0,05 est la valeur finale de la sortie pour une entrée en échelon unitaire. Cela correspond à une erreur en régime permanent de 0,95, ce qui est assez important. De plus, le temps de montée est d’environ une seconde, et le temps de descente d’environ 1,5 seconde. Concevons un contrôleur qui réduira le temps de montée, réduira le temps d’établissement, et éliminera l’erreur en régime permanent.
Commande proportionnelle
D’après le tableau présenté ci-dessus, nous voyons que la commande proportionnelle ( ) réduit le temps de montée, augmente le dépassement et réduit l’erreur en régime permanent.
) réduit le temps de montée, augmente le dépassement et réduit l’erreur en régime permanent.
La fonction de transfert en boucle fermée de notre système à rétroaction unitaire avec un contrôleur proportionnel est la suivante, où  est notre sortie (égale
est notre sortie (égale  ) et notre référence
) et notre référence  est l’entrée :
est l’entrée :
(7)
Laissons le gain proportionnel ( ) égal à 300 et modifions le fichier m-.par ce qui suit :
) égal à 300 et modifions le fichier m-.par ce qui suit :
Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.
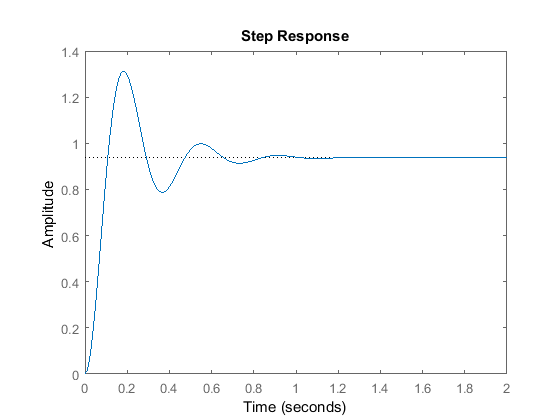
Le graphique ci-dessus montre que le contrôleur proportionnel a réduit à la fois le temps de montée et l’erreur en régime permanent, a augmenté le dépassement et a diminué le temps d’établissement d’une petite quantité.
Contrôle proportionnel-dérivé
Maintenant, jetons un coup d’œil au contrôle PD. D’après le tableau présenté ci-dessus, nous voyons que l’ajout de la commande dérivée ( ) tend à réduire à la fois le dépassement et le temps d’établissement. La fonction de transfert en boucle fermée du système donné avec un contrôleur PD est :
) tend à réduire à la fois le dépassement et le temps d’établissement. La fonction de transfert en boucle fermée du système donné avec un contrôleur PD est :
(8)
Laissons  égale à 300 comme précédemment et laissons
égale à 300 comme précédemment et laissons  égale à 10. Saisissez les commandes suivantes dans un fichier m et exécutez-le dans la fenêtre de commande MATLAB.
égale à 10. Saisissez les commandes suivantes dans un fichier m et exécutez-le dans la fenêtre de commande MATLAB.
Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.
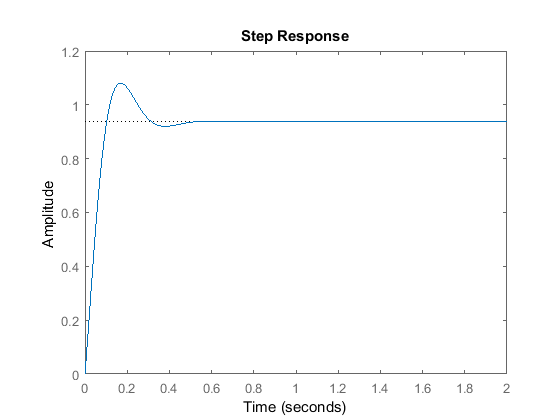
Ce graphique montre que l’ajout du terme dérivé a réduit à la fois le dépassement et le temps d’établissement, et a eu un effet négligeable sur le temps de montée et l’erreur en régime permanent.
Commande proportionnelle-intégrale
Avant de passer à la commande PID, étudions la commande PI. D’après le tableau, nous voyons que l’ajout d’une commande intégrale ( ) tend à diminuer le temps de montée, à augmenter à la fois le dépassement et le temps d’établissement, et à réduire l’erreur en régime permanent. Pour le système donné, la fonction de transfert en boucle fermée avec un contrôleur PI est :
) tend à diminuer le temps de montée, à augmenter à la fois le dépassement et le temps d’établissement, et à réduire l’erreur en régime permanent. Pour le système donné, la fonction de transfert en boucle fermée avec un contrôleur PI est :
(9)
Réduisons  à 30, et laissons
à 30, et laissons  égale à 70. Créez un nouveau fichier m et entrez les commandes suivantes .
égale à 70. Créez un nouveau fichier m et entrez les commandes suivantes .
Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.
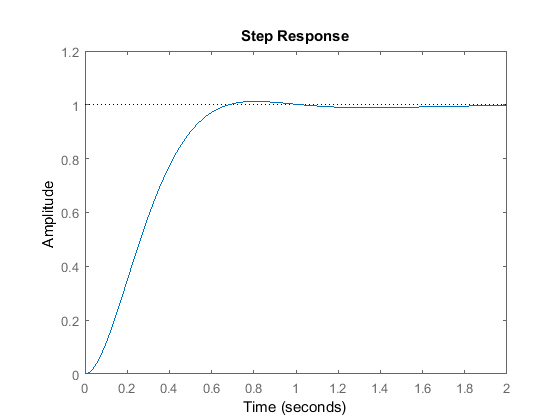
Exécutez ce fichier m dans la fenêtre de commande MATLAB et vous devriez générer le tracé ci-dessus. Nous avons réduit le gain proportionnel ( ) car le contrôleur intégral réduit également le temps de montée et augmente le dépassement comme le fait le contrôleur proportionnel (double effet). La réponse ci-dessus montre que le contrôleur intégral a éliminé l’erreur en régime permanent dans ce cas.
) car le contrôleur intégral réduit également le temps de montée et augmente le dépassement comme le fait le contrôleur proportionnel (double effet). La réponse ci-dessus montre que le contrôleur intégral a éliminé l’erreur en régime permanent dans ce cas.
Contrôleur proportionnel-intégral-dérivé
Maintenant, examinons le contrôle PID. La fonction de transfert en boucle fermée du système donné avec un contrôleur PID est:
(10)
Après plusieurs itérations de réglage, les gains 
 = 300, et
= 300, et  = 50 ont fourni la réponse souhaitée. Pour confirmer, entrez les commandes suivantes dans un fichier m et exécutez-le dans la fenêtre de commande. Vous devriez obtenir la réponse de l’étape suivante.
= 50 ont fourni la réponse souhaitée. Pour confirmer, entrez les commandes suivantes dans un fichier m et exécutez-le dans la fenêtre de commande. Vous devriez obtenir la réponse de l’étape suivante.
Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.
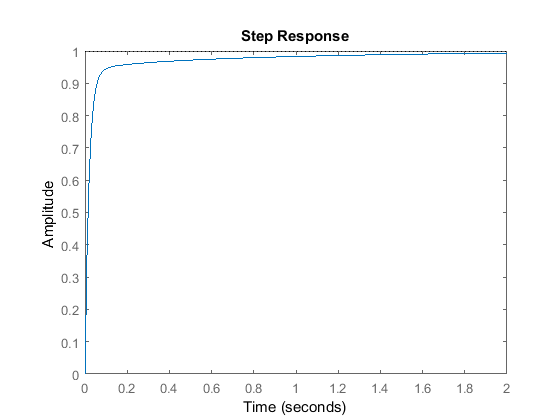
Maintenant, nous avons conçu un système en boucle fermée sans dépassement, avec un temps de montée rapide et sans erreur en régime permanent.
Conseils généraux pour la conception d’un contrôleur PID
Lorsque vous concevez un contrôleur PID pour un système donné, suivez les étapes indiquées ci-dessous pour obtenir une réponse souhaitée.
- Obtenir une réponse en boucle ouverte et déterminer ce qui doit être amélioré
- Ajouter une commande proportionnelle pour améliorer le temps de montée
- Ajouter une commande dérivée pour réduire le dépassement
- Ajouter une commande intégrale pour réduire l’erreur en régime permanent.state error
- Ajuste chacun des gains

 , et
, et  jusqu’à obtenir une réponse globale souhaitée. Vous pouvez toujours vous référer au tableau présenté dans cette page « Tutoriel PID » pour savoir quel contrôleur contrôle quelles caractéristiques.
jusqu’à obtenir une réponse globale souhaitée. Vous pouvez toujours vous référer au tableau présenté dans cette page « Tutoriel PID » pour savoir quel contrôleur contrôle quelles caractéristiques.
Enfin, gardez à l’esprit que vous n’avez pas besoin de mettre en œuvre les trois contrôleurs (proportionnel, dérivé et intégral) dans un seul système, si ce n’est pas nécessaire. Par exemple, si un contrôleur PI répond aux exigences données (comme l’exemple ci-dessus), alors vous n’avez pas besoin d’implémenter un contrôleur dérivé sur le système. Gardez le contrôleur aussi simple que possible.
Un exemple de réglage d’un contrôleur PI sur un système physique réel se trouve sur le lien suivant. Cet exemple commence également à illustrer certains défis de la mise en œuvre du contrôle, notamment : la saturation du contrôle, l’enroulement de l’intégrateur et l’amplification du bruit.
Réglage PID automatique
MATLAB fournit des outils pour choisir automatiquement les gains PID optimaux, ce qui rend inutile le processus d’essai et d’erreur décrit ci-dessus. Vous pouvez accéder à l’algorithme d’accord directement en utilisant pidtune ou par le biais d’une interface utilisateur graphique (GUI) agréable en utilisant pidTuner.
L’algorithme de réglage automatisé de MATLAB choisit les gains PID pour équilibrer les performances (temps de réponse, bande passante) et la robustesse (marges de stabilité). Par défaut, l’algorithme conçoit pour une marge de phase de 60 degrés.
Explorons ces outils automatisés en générant d’abord un contrôleur proportionnel pour le système masse-ressort-amortisseur en entrant la commande illustrée ci-dessous. Dans la syntaxe présentée, P est le modèle d’usine précédemment généré, et ‘p’ spécifie que le tuner emploie un contrôleur proportionnel.
pidTuner(P,'p')
La fenêtre de l’interface graphique de pidTuner, comme celle présentée ci-dessous, devrait apparaître.
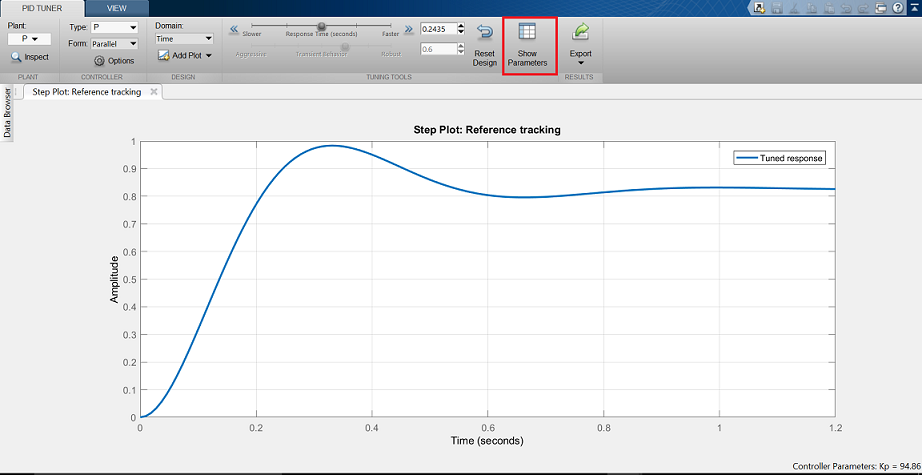
Notez que la réponse à l’échelon indiquée est plus lente que le contrôleur proportionnel que nous avons conçu à la main. Cliquez maintenant sur le bouton Afficher les paramètres en haut à droite. Comme prévu, le gain proportionnel,  , est plus petit que celui que nous avons employé,
, est plus petit que celui que nous avons employé,  < 300.
< 300.
Nous pouvons maintenant régler interactivement les paramètres du contrôleur et voir immédiatement la réponse résultante dans la fenêtre de l’interface graphique. Essayez de faire glisser le curseur du temps de réponse vers la droite jusqu’à 0,14 s, comme le montre la figure ci-dessous. Cela entraîne effectivement une accélération de la réponse, et nous pouvons voir  est maintenant plus proche de la valeur choisie manuellement. Nous pouvons également voir d’autres paramètres de performance et de robustesse pour le système. Notez qu’avant que nous ajustions le curseur, la marge de phase cible était de 60 degrés. Il s’agit de la valeur par défaut pour le pidTuner et elle fournit généralement un bon équilibre entre la robustesse et les performances.
est maintenant plus proche de la valeur choisie manuellement. Nous pouvons également voir d’autres paramètres de performance et de robustesse pour le système. Notez qu’avant que nous ajustions le curseur, la marge de phase cible était de 60 degrés. Il s’agit de la valeur par défaut pour le pidTuner et elle fournit généralement un bon équilibre entre la robustesse et les performances.

Essayons maintenant de concevoir un contrôleur PID pour notre système. En spécifiant le contrôleur ou (de base) précédemment conçu, C, comme deuxième paramètre, pidTuner concevra un autre contrôleur PID (au lieu de P ou PI) et comparera la réponse du système avec le contrôleur automatisé avec celle de la ligne de base.
pidTuner(P,C)
Nous voyons dans la fenêtre de sortie que le contrôleur automatisé répond plus lentement et présente plus de dépassement que la ligne de base. Choisissez maintenant l’option Domaine : Fréquence dans la barre d’outils, ce qui révèle les paramètres de réglage du domaine de fréquence.
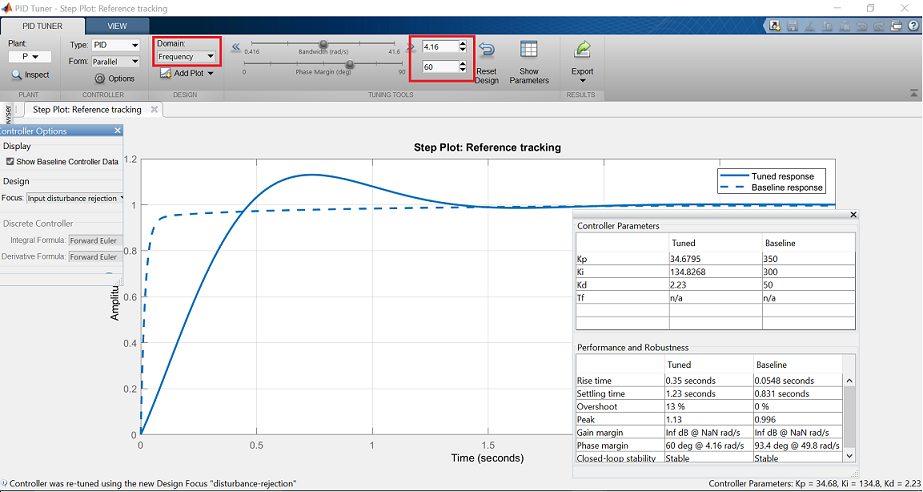
Tapez maintenant 32 rad/s pour la bande passante et 90 deg pour la marge de phase, afin de générer un contrôleur aux performances similaires à celles de la ligne de base. Gardez à l’esprit qu’une largeur de bande en boucle fermée plus élevée entraîne un temps de montée plus rapide, et qu’une marge de phase plus importante réduit le dépassement et améliore la stabilité du système.
Enfin, nous notons que nous pouvons générer le même contrôleur en utilisant l’outil de ligne de commande pidtune au lieu de l’interface graphique pidTuner en employant la syntaxe suivante.
opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90
Publié avec MATLAB® 9.2
.