Les calculs de TPP se font en jauge E, ce qui signifie que le champ laser est pris comme des ondes électromagnétiques. Le taux d’ionisation peut également être calculé en jauge A, qui met l’accent sur la nature particulaire de la lumière (absorption de plusieurs photons pendant l’ionisation). Cette approche a été adoptée par le modèle de Krainov basé sur les travaux antérieurs de Faisal et Reiss. Le taux résultant est donné par
W K R A = ∑ n = N ∞ 2 π ω 2 p ( n – n o s c ) 2 ∫ d Ω | F T ( I K A R Ψ ( r ) ) | 2 J n 2 ( n f , n o s c 2 ) W_{KRA}=\sum _{n=N}^{\i}infty }2\pi \omega ^{2}p\left(n-n{\mathrm {osc} }\right)^{2}\int \mathrm {d} \Omega \left|FT\left(I_{KAR}\Psi \left(\mathbf {r} \right)\right|^{2}J_{n}^{2}\left(n_{f},{\frac {n_{\mathrm {osc} }}{2}\right)}

où :
- n i = E i / ω , {\displaystyle n_{i}=E_{i}/\omega ,}
- n o s c = U p / ω {\displaystyle n_{\mathrm {osc}} }=U_{p}/\omega }
avec U p {\displaystyle U_{p}}
étant l’énergie pondéromotrice,
- N = {\displaystyle N=}
est le nombre minimal de photons nécessaires pour ioniser l’atome,
- J n ( u , v ) {\displaystyle J_{n}(u,v)}.
est la fonction de Bessel double,
- p = 2 ω ( n – n o s c – n i ) , {\displaystyle p={\sqrt {2\omega (n-n_{\mathrm {osc}}-n_{i})}},}
- n f = 2 n o s c / ω p cos ( θ ) {\displaystyle n_{f}=2{\sqrt {n_{\mathrm {osc}}}/\omega }}p={\sqrt {{\mathrm {osc}}}. }/\omega }}p\cos(\theta )}
avec θ {\displaystyle \theta }
l’angle entre la quantité de mouvement de l’électron, p, et le champ électrique du laser, F,
- FT est la transformée de Fourier tridimensionnelle, et
- I K A R = ( 2 Z 2 n 2 F r ) n {\displaystyle I_{KAR}=\left({\frac {2Z^{2}}{n^{2}Fr}\}\right)^{n}}.
incorpore la correction de Coulomb dans le modèle SFA.
Stabilisation atomique/piégeage de la populationEdit
Pour calculer le taux de MPI des atomes, seules les transitions vers les états du continuum sont considérées. Une telle approximation est acceptable tant qu’il n’y a pas de résonance multiphotonique entre l’état fondamental et certains états excités. Cependant, en situation réelle d’interaction avec des lasers pulsés, pendant l’évolution de l’intensité du laser, en raison du décalage de Stark différent des états fondamental et excité, il est possible que certains états excités entrent en résonance multiphotonique avec l’état fondamental. Dans le cadre de l’image de l’atome habillé, l’état fondamental habillé par m {\displaystyle m}.

photons et l’état résonant subissent un croisement évité à l’intensité de résonance I r {\displaystyle I_{r}}.

. La distance minimale, V m {\displaystyle V_{m}}

, au niveau du croisement évité est proportionnelle à la fréquence de Rabi généralisée, Γ ( t ) = Γ m I ( t ) m / 2 {\displaystyle \Gamma (t)=\Gamma _{m}I(t)^{m/2}}.

couplant les deux états. Selon Story et al, la probabilité de rester dans l’état fondamental, P g {\displaystyle P_{g}}.

, est donnée par P g = exp ( – 2 π W m 2 d W / d t ) {\displaystyle P_{g}=\exp \left(-{\frac {2\pi W_{m}^{2}{\mathrm {d} W/\mathrm {d} t}\right)}

où W {\displaystyle W}

est la différence d’énergie en fonction du temps entre les deux états habillés. En interaction avec une impulsion courte, si la résonance dynamique est atteinte dans la partie montante ou descendante de l’impulsion, la population reste pratiquement dans l’état fondamental et l’effet des résonances multiphotons peut être négligé. Cependant, si les états entrent en résonance au pic de l’impulsion, où d W / d t = 0 {\displaystyle \mathrm {d} W/\mathrm {d} t=0}

, alors l’état excité est peuplé. Après avoir été peuplé, comme le potentiel d’ionisation de l’état excité est faible, on s’attend à ce que l’électron soit instantanément ionisé.
En 1992, de Boer et Muller ont montré que des atomes de Xe soumis à de courtes impulsions laser pouvaient survivre dans les états hautement excités 4f, 5f et 6f . On pense que ces états ont été excités par le déplacement dynamique de Stark des niveaux en résonance multiphotonique avec le champ pendant la partie ascendante de l’impulsion laser. L’évolution ultérieure de l’impulsion laser n’a pas ionisé complètement ces états, laissant derrière elle quelques atomes hautement excités. Nous appellerons ce phénomène « piégeage de population ».

Nous mentionnons le calcul théorique selon lequel une ionisation incomplète se produit chaque fois qu’il y a une excitation résonante parallèle dans un niveau commun avec perte d’ionisation. Nous considérons un état tel que 6f de Xe qui consiste en 7 niveaux quasi-dégénérés dans la gamme de la largeur de bande du laser. Ces niveaux ainsi que le continuum constituent un système lambda. Le mécanisme du piégeage de type lambda est présenté schématiquement dans la figure. Au moment de la montée de l’impulsion (a), l’état excité (avec deux niveaux dégénérés 1 et 2) n’est pas en résonance multiphotonique avec l’état fondamental. L’électron est ionisé par couplage multiphotonique avec le continuum. Lorsque l’intensité de l’impulsion augmente, l’état excité et le continuum sont décalés en énergie en raison du décalage de Stark. Au pic de l’impulsion (b), les états excités entrent en résonance multiphotonique avec l’état fondamental. Lorsque l’intensité commence à diminuer (c), les deux états sont couplés par le continuum et la population est piégée dans une superposition cohérente des deux états. Sous l’action ultérieure de la même impulsion, en raison de l’interférence dans les amplitudes de transition du système lambda, le champ ne peut pas ioniser complètement la population et une fraction de la population sera piégée dans une superposition cohérente des niveaux quasi dégénérés. Selon cette explication, les états avec un moment angulaire plus élevé – avec plus de sous-niveaux – auraient une probabilité plus élevée de piéger la population. En général, la force du piégeage sera déterminée par la force du couplage à deux photons entre les niveaux quasi-dégénérés via le continuum. En 1996, en utilisant le laser très stable et en minimisant les effets de masquage de l’expansion de la région focale avec l’augmentation de l’intensité, Talebpour et al. ont observé des structures sur les courbes d’ions singulièrement chargés de Xe, Kr et Ar. Ces structures ont été attribuées au piégeage des électrons dans le fort champ laser. Une démonstration plus non ambiguë du piégeage de population a été rapportée par T. Morishita et C. D. Lin.
Ionisation multiple non séquentielleEdit
Le phénomène d’ionisation non séquentielle (NSI) d’atomes exposés à des champs laser intenses a fait l’objet de nombreuses études théoriques et expérimentales depuis 1983. Les travaux pionniers ont commencé avec l’observation d’une structure en « genou » sur la courbe du signal de l’ion Xe2+ en fonction de l’intensité par L’Huillier et al. Du point de vue expérimental, la double ionisation NS fait référence à des processus qui, d’une manière ou d’une autre, augmentent le taux de production d’ions doublement chargés par un facteur énorme à des intensités inférieures à l’intensité de saturation de l’ion singulièrement chargé. Beaucoup, en revanche, préfèrent définir la double ionisation NS comme un processus par lequel deux électrons sont ionisés presque simultanément. Cette définition implique qu’en dehors du canal séquentiel A + L – > A + + L – > A + + {\displaystyle A+L->A^{+}+L->A^{++}}.

il existe une autre chaîne A + L – > A + + {\displaystyle A+L->A^{++}}

qui est la principale contribution à la production d’ions doublement chargés à des intensités plus faibles. La première observation d’un triple INS dans l’argon interagissant avec un laser de 1 µm a été rapportée par Augst et al. Plus tard, en étudiant systématiquement l’INS de tous les atomes de gaz rares, le quadruple INS du Xe a été observé. La conclusion la plus importante de cette étude a été l’observation de la relation suivante entre le taux de NSI à tout état de charge et le taux d’ionisation tunnel (prédit par la formule ADK) aux états de charge précédents ; W N S ( A n + ) = ∑ i = 1 n – 1 α n ( λ ) W A D K ( A i + ) {\displaystyle W_{NS}(A^{n+})=\sum _{i=1}^{n-1}\alpha _{n}\left(\lambda \right)W_{ADK}\left(A^{i+}\right)}

où W A D K ( A i + ) {\displaystyle W_{ADK}\left(A^{i+}\right)}

est le taux d’effet tunnel quasi-statique vers le i’ième état de charge et α n ( λ ) {\displaystyle \alpha _{n}(\lambda )}.

sont des constantes dépendant de la longueur d’onde du laser (mais pas de la durée de l’impulsion).
Deux modèles ont été proposés pour expliquer l’ionisation non séquentielle ; le modèle shake-off et le modèle de rediffusion des électrons. Le modèle shake-off (SO), proposé pour la première fois par Fittinghoff et al, est adopté dans le domaine de l’ionisation des atomes par les rayons X et les projectiles électroniques où le processus SO est l’un des principaux mécanismes responsables de l’ionisation multiple des atomes. Le modèle SO décrit le processus NS comme un mécanisme dans lequel un électron est ionisé par le champ laser et le départ de cet électron est si rapide que les électrons restants n’ont pas le temps de s’adapter aux nouveaux états d’énergie. Par conséquent, il existe une certaine probabilité qu’après l’ionisation du premier électron, un deuxième électron soit excité vers des états d’énergie plus élevée (shake-up) ou même ionisé (shake-off). Mentionnons que, jusqu’à présent, il n’y a pas eu de calcul quantitatif basé sur le modèle SO, et le modèle reste qualitatif.
Le modèle de rediffusion des électrons a été développé indépendamment par Kuchiev, Schafer et al, Corkum, Becker et Faisal et Faisal et Becker. Les principales caractéristiques du modèle peuvent être facilement comprises à partir de la version de Corkum. Le modèle de Corkum décrit l’ionisation NS comme un processus par lequel un électron est ionisé par effet tunnel. L’électron interagit ensuite avec le champ laser où il est accéléré pour s’éloigner du noyau nucléaire. Si l’électron a été ionisé à une phase appropriée du champ, il passera par la position de l’ion restant un demi-cycle plus tard, où il pourra libérer un électron supplémentaire par impact électronique. Dans la moitié des cas seulement, l’électron est libéré à la phase appropriée et dans l’autre moitié, il ne retourne jamais au cœur nucléaire. L’énergie cinétique maximale que peut avoir l’électron de retour est de 3,17 fois le potentiel pondéromoteur ( U p {\displaystyle U_{p}}.

) du laser. Le modèle de Corkum place une limite de coupure de l’intensité minimale ( U p {\displaystyle U_{p}}

est proportionnelle à l’intensité) où une ionisation due à la rediffusion peut se produire.
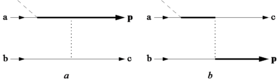
Le modèle de rediffusion dans la version de Kuchiev (modèle de Kuchiev) est mécanique quantique. L’idée de base du modèle est illustrée par les diagrammes de Feynman de la figure a. Tout d’abord, les deux électrons sont dans l’état fondamental d’un atome. Les lignes marquées a et b décrivent les états atomiques correspondants. Ensuite, l’électron a est ionisé. Le début du processus d’ionisation est représenté par l’intersection avec une ligne pointillée inclinée. où le MPI se produit. La propagation de l’électron ionisé dans le champ laser, pendant laquelle il absorbe d’autres photons (ATI), est représentée par la ligne épaisse pleine. La collision de cet électron avec l’ion atomique parent est illustrée par une ligne pointillée verticale représentant l’interaction coulombienne entre les électrons. L’état marqué par c décrit l’excitation de l’ion vers un état discret ou continu. La figure b décrit le processus d’échange. Le modèle de Kuchiev, contrairement à celui de Corkum, ne prévoit aucune intensité seuil pour l’apparition de l’ionisation NS.
Kuciev n’a pas inclus les effets coulombiens sur la dynamique de l’électron ionisé. Cela a entraîné une sous-estimation du taux de double ionisation par un facteur énorme. Évidemment, dans l’approche de Becker et Faisal (qui est équivalente au modèle de Kuchiev dans l’esprit), cet inconvénient n’existe pas. En fait, leur modèle est plus exact et ne souffre pas du grand nombre d’approximations faites par Kuchiev. Les résultats de leurs calculs correspondent parfaitement aux résultats expérimentaux de Walker et al. Becker et Faisal ont pu ajuster les résultats expérimentaux sur les NSI multiples des atomes de gaz rares en utilisant leur modèle. En conséquence, la rediffusion des électrons peut être prise comme le mécanisme principal pour l’apparition du processus NSI.
Ionisation multiphotonique des électrons de valence interne et fragmentation des molécules polyatomiquesEdit
L’ionisation des électrons de valence interne sont responsables de la fragmentation des molécules polyatomiques dans les champs laser forts. Selon un modèle qualitatif, la dissociation des molécules se produit par un mécanisme en trois étapes :
- MPI des électrons des orbitales internes de la molécule qui aboutit à un ion moléculaire dans les niveaux ro-vibrationnels d’un état électronique excité ;
- Transition rapide sans rayonnement vers les niveaux ro-vibrationnels de haute altitude d’un état électronique inférieur ; et
- Dissociation subséquente de l’ion en différents fragments par divers canaux de fragmentation.







