La transformée de Fourier (FT) décompose un signal en fréquences qui le composent.
Qu’est-ce que cela signifie ?
Par exemple. Admettons que nous ayons un signal S1.

Si nous voulons mesurer la force de ce signal à un moment précis. Nous le mesurons par son amplitude.
Donc, l’amplitude du signal S1 est de 1
Si nous faisons la même chose pour un autre signal et choisissons le même moment dans le temps et nous mesurons son amplitude. Soit un autre signal S2 comme ceci

Alors, l’amplitude du signal S2 est de 2
Maintenant, que se passe-t-il lorsque nous émettons ces deux signaux en même temps (S1 et S2) ?
Donc, lorsque nous émettons ces deux signaux au même instant, nous obtenons un nouveau signal qui est la somme de l’amplitude de ces deux signaux. Il en est ainsi parce que ces deux signaux sont additionnés.

So, l’amplitude de S3 = amplitude de S1 + amplitude de S2 = 1 + 2 = 3
Donc, l’amplitude du signal S3 est de 3
Maintenant, la question intéressante est :
Si on nous donne uniquement le signal S3 (qui est la somme des signaux S1 et S2).Peut-on récupérer les signaux originaux S1 et S2 ?
Oui, c’est ce que fait une transformée de Fourier. Elle reprend un signal et le décompose en fréquences qui l’ont constitué.
Dans notre exemple, une transformée de Fourier décomposerait le signal S3 en fréquences constitutives comme les signaux S1 et S2
Mais, Comment peut-on récupérer les signaux originaux ? Que va faire la transformée de Fourier pour nous ?

Disons que les trois signaux de l’image ci-dessus sont S1, S2, et S3 et lorsque nous fusionnons ces trois signaux ensemble, nous obtenons le signal en rouge qui est en fait la somme des trois signaux S1+S2+S3.
Ce que fait la transformée de Fourier, c’est qu’elle nous fait en quelque sorte passer du domaine temporel au domaine fréquentiel.
Au cas où, Si quelqu’un se demande, Et si nous voulons revenir du domaine fréquentiel au domaine temporel ?
Nous pouvons le faire en utilisant la transformée de Fourier inverse(IFT). Mais nous n’en parlerons pas dans cet article.
Génération de signal et déphasage
Si nous voulons décrire un signal, nous avons besoin de trois choses :
- La fréquence du signal qui montre, combien d’occurrences dans la période que nous avons.
- L’amplitude qui montre la hauteur du signal ou en d’autres termes la force du signal.
- Le déphasage comme où commence le signal.
Le tout premier exemple que nous avons pris était très simple, chaque signal avait la même fréquence et la même différence de phase et seulement des amplitudes différentes.
Nous allons maintenant examiner un exemple légèrement plus complexe et nous allons examiner le signal individuel de l’exemple ci-dessus car pour mieux comprendre la transformée de Fourier, nous devons examiner de près les signaux individuels.
Vous trouverez ci-dessous les signaux originaux que nous regardions ci-dessus.

.


Fréquence : Si nous regardons de près les trois signaux, nous remarquerons que la fréquence des trois signaux est différente.
Si pour une même période de temps, dans le signal 1 il y a un nombre n de vagues alors il y a 2n nombre de vagues dans le signal 2 et vice versa.
Phase : De plus, lorsque nous regardons de près pour savoir où commence réellement le signal. Nous trouverons que tandis que le signal 1 commence à (0,0), le signal 2 commence à (-0,5,0) si nous traçons l’onde pour rencontrer l’axe des y à 0. Donc, à 0, nous avons déjà l’amplitude maximale du signal. C’est ce que nous appelons le déphasage.
Amplitude : Les trois signaux ont des amplitudes différentes, le signal 1 a une amplitude de 1 tandis que le signal 2 et le signal 3 ont une amplitude de 2 et 3 respectivement.
Tout cela est capturé dans une formule mathématique élégante et super simple. Donc, Dans les exemples ci-dessus si l’axe des x est appelé x et l’axe des y est appelé y. Nous pouvons générer y en fonction de t tel que :

En utilisant cette formule, nous pouvons générer n’importe quel type de signal que nous voulons et ensuite nous pouvons les fusionner ensemble et jouer avec eux. Par exemple, si nous fusionnons les signaux 1, 2 et 3. nous obtiendrons un signal comme celui-ci :

Les mathématiques derrière la transformée de Fourier
L’idée principale derrière la transformée de Fourier est que :
Tout signal continu dans le domaine temporel peut être représenté de manière unique et non ambiguë par une série infinie de sinusoïdes.
Que cela signifie-t-il ?
Cela signifie que, si nous avons un signal et que ce signal est généré par une certaine fonction x(t) alors nous pouvons trouver une autre fonction f(t) telle que :

Donc, Peu importe la force du signal, on peut trouver une fonction comme f(t) qui est une somme d’une série infinie de sinusoïdes qui représentera effectivement parfaitement le signal.
Maintenant, la question qui se pose est de savoir comment trouver les coefficients ici dans l’équation ci-dessus car ce sont les valeurs qui détermineraient la forme de la sortie et donc du signal.
Donc, pour obtenir ces coefficients, nous utilisons des transformées de Fourier et le résultat de la transformée de Fourier est un groupe de coefficients. Ainsi, nous utilisons X(F) pour désigner les coefficients de Fourier et c’est une fonction de la fréquence que nous obtenons en résolvant l’intégrale telle que :
.
La partie délicate dans cette intégrale est en fait le i qui désigne un nombre complexe. Ainsi, on se souvient probablement que i² = -1 ou i = √-1. Il peut également être utile de se rappeler que la forme d’un nombre complexe est a + ib . Il possède donc une partie réelle et une partie imaginaire.
Aussi, lorsque nous résolvons réellement l’intégrale ci-dessus, nous obtenons ces nombres complexes où a et b correspondent aux coefficients que nous recherchons.
Nous avons cependant trois problèmes à traiter :
- Comment traiter
i. - Comment traiter les signaux discrets.
Donc, commençons par le deuxième.
Pour comprendre la transformée de Fourier discrète, nous devons d’abord comprendre comment échantillonner un signal continu ?
Selon Wikipédia, En traitement du signal, l’échantillonnage est la réduction d’un signal à temps continu en un signal à temps discret. Voici un exemple de la façon dont la forme du signal change avec la modification du taux d’échantillonnage :
Disons que le signal original est un signal d’une amplitude de deux et d’une fréquence de cinq sur une période d’une seconde :
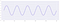
.
Maintenant, lorsque nous diminuons le taux d’échantillonnage, regardons comment la forme du signal change :
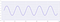
.
A mesure que l’on diminue encore la fréquence d’échantillonnage, nous obtenons :

.
Donc, l’essentiel est : Plus le taux d’échantillonnage est élevé, meilleure est la qualité du signal et aussi nous pouvons distinguer plus de fréquences.
Maintenant, que nous savons comment échantillonner les signaux, nous allons regarder la modification des algorithmes connus sous le nom de Transformée de Fourier Discrète.
Transformation de Fourier discrète
Tout signal échantillonné de longueur N dans le domaine temporel peut être représenté de manière unique et non ambiguë par une série finie de sinusoïdes.
Donc, Nous n’avons plus à traiter de l’infini dans notre nouvelle définition.
Quelle est la différence ?
Dans la transformation de Fourier standard, nous avons utilisé une fonction du temps x(t) pour générer un signal continu. Maintenant Dans le cas discret, nous n’avons pas de fonction, nous avons un ensemble de données, un ensemble de points que nous obtenons en échantillonnant le signal continu. Donc, je vais utiliser {x} pour donner un ensemble de données tel qu’il contient la lecture de l’échantillonnage tel que :
et ce que va faire la Transformée de Fourier Discrète. Transform va faire pour nous, c’est qu’elle va transformer le jeu de données de {x} en un autre jeu de données {X} qui contiendra les coefficients de Fourier tels que :

Si l’on regarde la définition de la transformée de Fourier, chaque X dans {X} est un nombre complexe et il contient les a et b composantes pour les fréquences.
Mais, comment se fait-il que les deux ensembles de données {x} et {X} aient la même longueur ?
Si l’on réfléchit, ce qui motive la longueur de l’ensemble de données {x} est le taux d’échantillonnage car, sur une période de temps, le nombre de points de données que je lis est exactement le taux d’échantillonnage n’est-ce pas ? Si nous pensons à l’autre ensemble de données {X} , nous avons dit que la fréquence est le nombre d’occurrences par unité de temps. Donc, si j’échantillonne avec une certaine fréquence, je ne peux pas reconnaître les signaux qui ont une fréquence plus grande que la fréquence d’échantillonnage simplement parce que nous n’avons pas assez de points de données.
Donc, si nous avons des signaux avec des fréquences très élevées sur un taux d’échantillonnage très faible, nous ne pourrons pas du tout reconnaître ces signaux. Donc, le nombre de fréquences que nous pouvons reconnaître en appliquant la transformée de Fourier est en fait piloté par le taux d’échantillonnage également.
Donc, maintenant que nous avons notre ensemble de données {x} nous allons obtenir {Xk} tel qu’il est un élément dans {X} qui sont mes coefficients de Fourier tels que :
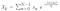
.
So, c’est essentiellement la Transformée de Fourier Discrète. Nous pouvons faire ce calcul et il produira un nombre complexe sous la forme a + ib où nous avons deux coefficients pour la série de Fourier.
Maintenant, nous savons comment échantillonner des signaux et comment appliquer une transformation de Fourier discrète. La dernière chose que nous aimerions faire est, nous aimerions nous débarrasser du nombre complexe i parce qu’il n’est pas supporté dans mllib ou systemML en utilisant quelque chose connu sous le nom de formule d’Euler qui stipule :
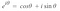
Donc, Si on introduit la formule d’Euler dans l’équation de la transformation de Fourier, nous obtenons

nous savons également que cos(-θ) = cos(θ) et sin(-θ) = -sin(θ) et si nous utilisons ceci dans l’équation ci-dessus, l’équation pourrait être simplifiée comme suit :

.
et nous pouvons en fait décomposer l’équation ci-dessus en deux sommes, telles que :

Maintenant, Si nous comparons l’équation ci-dessus avec l’équation d’un nombre complexe qui est a + ib alors nous obtenons la valeur correspondante comme :
So, nous pouvons maintenant mettre ces valeurs dans l’équation de f(t) et obtenir le résultat.
Conclusion
En pratique, nous utilisons une légère modification de la transformée de Fourier discrète connue sous le nom de transformée de Fourier rapide car la transformée de Fourier discrète est très simple, basique et aussi lente. Elle n’est pas adaptée au but recherché si nous voulons vraiment faire quelque chose dans un environnement de production. La complexité de calcul de la transformée de Fourier discrète est un temps quadratique O(n²) et la transformée de Fourier rapide pour comparaison est un temps quasi-linéaire O(nlogn). La transformation de Fourier rapide fait cela en exploitant l’assymétrie dans la transformation de Fourier.