Les Égyptiens disposaient d’un système d’écriture basé sur les hiéroglyphes à partir d’environ 3000 avant JC. Les hiéroglyphes sont de petites images représentant des mots. Il est facile de voir comment ils désignaient le mot « oiseau » par une petite image d’un oiseau, mais il est clair que sans développement ultérieur, ce système d’écriture ne peut pas représenter de nombreux mots. Le moyen de contourner ce problème adopté par les anciens Égyptiens était d’utiliser les sons parlés des mots. Par exemple, pour illustrer l’idée avec une phrase anglaise, nous pouvons voir comment « I hear a barking dog » pourrait être représenté par :
Bien sûr, les mêmes symboles pourraient signifier quelque chose de différent dans un contexte différent, ainsi « un œil » pourrait signifier « voir » tandis que « une oreille » pourrait signifier « son ».
Les Égyptiens avaient un système de base 10 de hiéroglyphes pour les chiffres. Nous entendons par là qu’ils ont des symboles distincts pour une unité, une dizaine, une centaine, un millier, une dizaine de milliers, une centaine de milliers et un million.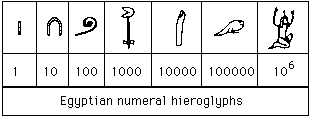
Voici les hiéroglyphes des chiffres.
Pour composer le nombre 276, par exemple, quinze symboles étaient nécessaires : deux symboles « cent », sept symboles « dix » et six symboles « unité ». Les chiffres apparaissaient ainsi :
276 en hiéroglyphes.
Voici un autre exemple :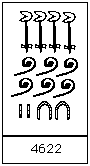
4622 en hiéroglyphes.
Notez que les exemples de 276 et 4622 en hiéroglyphes sont vus sur une sculpture en pierre de Karnak, datant d’environ 1500 avant JC, et maintenant exposée au Louvre à Paris.
Comme on peut facilement le voir, ajouter des hiéroglyphes numéraux est facile. Il suffit d’ajouter les différents symboles, mais en remplaçant dix exemplaires d’un symbole par un seul symbole de la valeur immédiatement supérieure. Pour les Égyptiens de l’Antiquité, les fractions se limitaient aux fractions unitaires (à l’exception de la 23\large\frac{2}{3}\normalsize32 fréquemment utilisée et de la 34\large\frac{3}{4}\normalsize43 moins fréquemment utilisée). Une fraction unitaire est de la forme 1n\large\frac{1}{n}\normalsizen1 où nnn est un nombre entier et ceux-ci étaient représentés dans les hiéroglyphes numéraux en plaçant le symbole représentant une « bouche », qui signifiait « partie », au-dessus du nombre. Voici quelques exemples :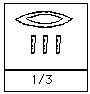
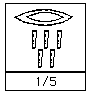
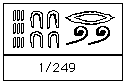
Notez que lorsque le nombre contenait trop de symboles pour que le signe « partie » soit placé au-dessus du nombre entier, comme dans 1249\large\frac{1}{249}\normalsize2491, alors le symbole « partie » était juste placé sur la « première partie » du nombre.
Nous devons préciser que les hiéroglyphes ne sont pas restés les mêmes pendant les quelque deux mille ans de la civilisation égyptienne antique. Cette civilisation est souvent décomposée en trois périodes distinctes :
Ancien royaume – environ 2700 av. J.-C. à 2200 av. J.-C.
Moyen royaume – environ 2100 av. J.-C. à 1700 av. J.-C.
Nouveau royaume – environ 1600 av. J.-C. à 1000 av. J.-C.
Les hiéroglyphes numéraux étaient quelque peu différents à ces différentes périodes, mais conservaient un style globalement similaire.
Un autre système de numération, que les Égyptiens ont utilisé après l’invention de l’écriture sur papyrus, était composé de chiffres hiératiques. Ces chiffres permettaient d’écrire les nombres sous une forme beaucoup plus compacte ; cependant, l’utilisation de ce système nécessitait la mémorisation de beaucoup plus de symboles. Il y avait des symboles séparés pour
10, 20, 30, 40, 50, 60, 70, 80, 90,
100, 200, 300, 400, 500, 600, 700, 800, 900,
1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000
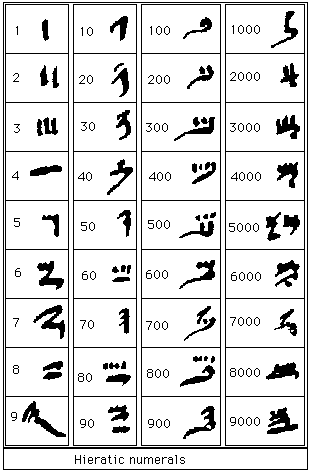
Voici des versions des chiffres hiératiques
Avec ce système, les nombres pouvaient être formés de quelques symboles. Le nombre 9999 ne comportait que 4 symboles hiératiques au lieu de 36 hiéroglyphes. Une différence majeure entre les chiffres hiératiques et notre propre système numérique était que les chiffres hiératiques ne formaient pas un système positionnel, donc les chiffres particuliers pouvaient être écrits dans n’importe quel ordre.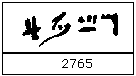
Voici une façon dont les Égyptiens ont écrit 2765 en chiffres hiératiques 
Voici une deuxième façon d’écrire 2765 en chiffres hiératiques avec l’ordre inversé
Comme les hiéroglyphes, les symboles hiératiques ont changé avec le temps mais ils ont subi plus de changements avec six périodes distinctes. Au départ, les symboles utilisés étaient assez proches du hiéroglyphe correspondant mais leur forme a divergé avec le temps. Les versions que nous donnons des chiffres hiératiques datent d’environ 1800 avant Jésus-Christ. Les deux systèmes ont fonctionné en parallèle pendant environ 2000 ans, les symboles hiératiques étant utilisés pour l’écriture sur papyrus, comme par exemple dans le papyrus Rhind et le papyrus Moscow, tandis que les hiéroglyphes continuaient à être utilisés pour la gravure sur pierre.