LEERDOELSTELLINGEN
Aan het eind van dit deel zul je in staat zijn om:
- Uitleggen wat een continue bron ladingsverdeling is en hoe het samenhangt met het concept van kwantisatie van lading
- Lijnladingen, oppervlakteladingen en volumeladingen beschrijven
- Het veld berekenen van een continue bron ladingsverdeling van elk teken
De ladingsverdelingen die we tot nu toe hebben gezien waren discreet: opgebouwd uit individuele puntdeeltjes. Dit in tegenstelling tot een continue ladingsverdeling, die ten minste één dimensie heeft die niet nul is. Als een ladingsverdeling continu is in plaats van discreet, kunnen we de definitie van het elektrisch veld veralgemenen. We verdelen de lading eenvoudigweg in infinitesimale stukjes en behandelen elk stukje als een puntlading.
Merk op dat, omdat lading gekwantiseerd is, er niet zoiets bestaat als een “echt” continue ladingsverdeling. Maar in de meeste praktische gevallen bestaat de totale lading die het veld creëert uit zo’n groot aantal discrete ladingen dat we veilig het discrete karakter van de lading kunnen negeren en het als continu kunnen beschouwen. Dit is precies de benadering die we maken als we een emmer water beschouwen als een continue vloeistof, in plaats van een verzameling moleculen.
Onze eerste stap is het definiëren van een ladingsdichtheid voor een ladingsverdeling langs een lijn, over een oppervlak, of binnen een volume, zoals in figuur
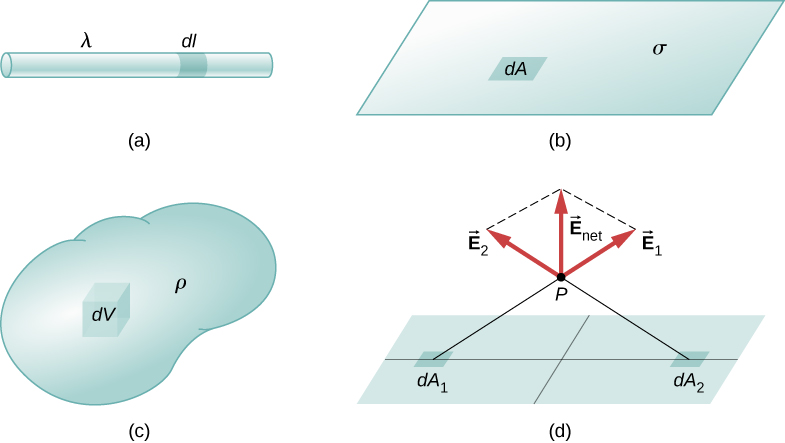
Definities: Laaddichtheden
Definities van ladingsdichtheid:
- lineaire ladingsdichtheid: \lading per lengte-eenheid (figuur); eenheden zijn coulomb per meter (C/m))
- oppervlakteladingsdichtheid: \lading per oppervlakte-eenheid (figuur); eenheden zijn coulomb per vierkante meter (C/m^2)
- volumeladingsdichtheid: \lading per volume-eenheid (figuur \PageIndex{1c}); eenheden zijn coulomb per vierkante meter (C/m^3)
Voor een lijnlading, een oppervlaktelading, en een volumelading wordt de sommatie in de eerder besproken definitie van een elektrisch veld een integraal en wordt \(q_i) vervangen door respectievelijk \(dq = \lambda dl), \(\sigma dA), of \(\rho dV):
Verwachte{E}(P) &= \onderbrace{\dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{lambda \, dl}{r^2}}rechts) \hat{r}}_{text{Lijnlading}} \label{eq2} &= \underbrace{dfrac{1}{4pi \epsilon_0} …\int_{surface}… \links(\dfrac{\sigma \,dA}{r^2}}rechts) \hat{r} }_{\text{Surface charge}}\label{eq3} &= \underbrace{dfrac{1}{4pi \epsilon_0} \. \left(\dfrac{\rho \,dV}{r^2}}rechts) \hat{r}}_{text{Volume lading}} {\label{eq4}
De integralen in vergelijkingen \ref{eq1}-\ref{eq4} zijn generalisaties van de uitdrukking voor het veld van een puntlading. Ze bevatten impliciet het principe van superpositie en gaan daar ook van uit. De “truc” om ze te gebruiken is bijna altijd om met correcte uitdrukkingen te komen voor (dl), (dA), of (dV), naargelang het geval, uitgedrukt in termen van r, en ook om de ladingsdichtheidsfunctie op de juiste manier uit te drukken. Het kan constant zijn; het kan afhankelijk zijn van de plaats.
Neem zorgvuldig de betekenis van r in deze vergelijkingen: Het is de afstand van het ladingselement (q_i, libda, dl, sigma, dA, rho, dV) tot de plaats van belang, P(x, y, z) (het punt in de ruimte waar je het veld wilt bepalen). Verwar dit echter niet met de betekenis van \(\wat{r}}); we gebruiken deze en de vector-notatie \(\vec{E}}) om drie integralen in één keer te schrijven. Dat wil zeggen, vergelijking \ref{eq2} is eigenlijk
E_y(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \_y, E_z(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \links(\dfrac{lambda}, dl}{r^2}rechts)_z \eind{align}
Exemplaar (Pagina-index{1}): Elektrisch veld van een lijnstuk
Bepaal het elektrisch veld op een afstand z boven het middelpunt van een recht lijnstuk met lengte L dat een uniforme lineaire ladingsdichtheid heeft.
Strategie
Omdat dit een continue ladingsverdeling is, breken we het draadsegment conceptueel op in differentiële stukken van lengte \(dl\), die elk een differentiële hoeveelheid lading dragen
Daarna berekenen we het differentiële veld dat ontstaat door twee symmetrisch geplaatste stukken van de draad, gebruikmakend van de symmetrie van de opstelling om de berekening te vereenvoudigen (figuur \(\PageIndex{2})). Tenslotte integreren we deze uitdrukking van het differentiaalveld over de lengte van de draad (de helft eigenlijk, zoals we hieronder uitleggen) om de volledige uitdrukking van het elektrisch veld te verkrijgen.
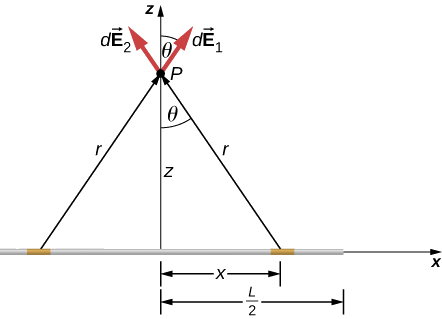
Oplossing
Voordat we er induiken, hoe verwacht men dat het veld er van veraf “uitziet”? Omdat het een eindig lijnstuk is, moet het er van veraf uitzien als een puntlading. We zullen de uitdrukking die we krijgen controleren om te zien of die aan deze verwachting voldoet.
Het elektrisch veld voor een lijnlading wordt gegeven door de algemene uitdrukking
De symmetrie van de situatie (onze keuze van de twee identieke differentiële stukken lading) impliceert dat de horizontale (x)-componenten van het veld opheffen, zodat het netto veld in de (z)-richting wijst. Laten we dit formeel controleren.
Het totale veld \(\vec{E}(P)\) is de vectorsom van de velden van elk van de twee ladingselementen (noem ze voorlopig \(\vec{E}_1) en \(\vec{E}_2)):
&= E_{1x}\hat{i} + E_{1z}\Wat{k} + E_{2x} (-{hat{i}) + E_{2z}}\Dat{k}.
Omdat de twee ladingselementen identiek zijn en op dezelfde afstand liggen van het punt waar we het veld willen berekenen, \(E_{1x} = E_{2x}}), heffen die componenten op. Dan blijft over
&= E_1 \, \cos \, \theta \hat{k} + E_2 \, \cos \, \theta \hat{k}.
Deze componenten zijn ook gelijk, dus geldt
&= \dfrac{1}{4 \pi \epsilon_0} \int_0^{L/2} \dfrac{2lambda dx}{r^2} \, \cos \, \theta \hat{k}
waarin ons differentiaalelement dl in dit voorbeeld dx is, omdat we integreren langs een lijn van lading die op de x-as ligt. (De grenzen van de integratie zijn 0 tot \(\frac{L}{2}}), niet \(-\frac{L}{2}}) tot \(+\frac{L}{2}}), omdat we het netto veld hebben opgebouwd uit twee differentiële stukken lading \(dq\)). Als we over de hele lengte zouden integreren, zouden we een foutieve factor 2 krijgen.)
In principe is dit volledig. Maar om deze integraal te berekenen, moeten we alle variabelen elimineren die niet gegeven zijn. In dit geval veranderen zowel r als t als we naar buiten integreren naar het eind van de lineaire lading, dus dat zijn de variabelen die we weg moeten werken. We kunnen dat doen op dezelfde manier als we deden voor de twee puntladingen: door op te merken dat
en
Substitueren, krijgen we
&= \dfrac{1}{4 \pi \epsilon_0} {int_0^{L/2} \dfrac{2}lambda z}{(z^2 + x^2)^{3/2}} dx \hat{k} &= \dfrac{2 \lambda z}{4 \pi \epsilon_0} \left_0^{L/2} \hat{k}.
Wat vereenvoudigt tot
Belang
Merk opnieuw het gebruik van symmetrie om het probleem te vereenvoudigen. Dit is een zeer gebruikelijke strategie voor het berekenen van elektrische velden. De velden van niet-symmetrische ladingsverdelingen moeten worden behandeld met meervoudige integralen en moeten eventueel numeriek worden berekend door een computer.
PageIndex{1})
Hoe zou de hierboven gebruikte strategie veranderen om het elektrisch veld te berekenen in een punt op een afstand \(z\) boven een uiteinde van het eindige lijnstuk?
Antwoord
We zullen niet langer gebruik kunnen maken van de symmetrie. In plaats daarvan moeten we elk van de twee componenten van het elektrisch veld met hun eigen integraal berekenen.
Voorbeeld (\PageIndex{2}\): Elektrisch veld van een oneindige ladingslijn
Vind het elektrisch veld op een afstand \(z) boven het middelpunt van een oneindige ladingslijn die een uniforme lineaire ladingsdichtheid draagt \(\lambda\).
Strategie
Dit is precies als het vorige voorbeeld, behalve dat de grenzen van de integratie \(-infty) tot \(+infty) zullen zijn.
Oplossing
Wederom heffen de horizontale componenten op, zodat we uitkomen op
waarbij ons differentiaallijnelement dl in dit voorbeeld dx is, omdat we integreren langs een lijn van lading die op de x-as ligt. Nogmaals,
&= \dfrac{z}{(z^2 + x^2)^{1/2}}. \eind{align*}
Substitueren, dan krijgen we
&= \dfrac{1}{4 \pi \epsilon_0} \int_{-\infty}^{\infty} \dfrac{lambda z}{(z^2 + x^2)^{3/2}}dx \hat{k}} &= \dfrac{1}{4 \pi \epsilon_0} \left_{-\infty}^{\infty} \, \hat{k}
wat vereenvoudigt tot
Belang
Onze strategie voor het werken met continue ladingsverdelingen geeft ook bruikbare resultaten voor ladingen met oneindige dimensie.
In het geval van een eindige ladingslijn zien we dat voor z^2 de L in de noemer overheerst, zodat vergelijking 5.12} vereenvoudigt tot
Als je je herinnert dat \lambda L = q) de totale lading op de draad is, dan hebben we de uitdrukking voor het veld van een puntlading, zoals verwacht.
In de limiet ²(L = q) krijgen we echter het veld van een oneindige rechte draad, dat is een rechte draad waarvan de lengte veel, veel groter is dan een van zijn andere afmetingen, en ook veel, veel groter dan de afstand waarop het veld moet worden berekend:
Een interessant artefact van deze oneindige limiet is dat we de gebruikelijke afhankelijkheid van r^2 die we gewend zijn, kwijt zijn. Dit wordt nog intrigerender in het geval van een oneindig vlak.
Voorbeeld \PageIndex{3A}\): Elektrisch veld door een ring van lading
Een ring heeft een uniforme ladingsdichtheid, met eenheden van coulomb per boogmeter. Bereken het elektrisch veld in een punt op de as die door het centrum van de ring gaat.
Strategie
We gebruiken dezelfde procedure als voor de geladen draad. Het verschil hier is dat de lading is verdeeld over een cirkel. We verdelen de cirkel in infinitesimale elementen in de vorm van bogen op de cirkel en gebruiken poolcoördinaten zoals in figuur
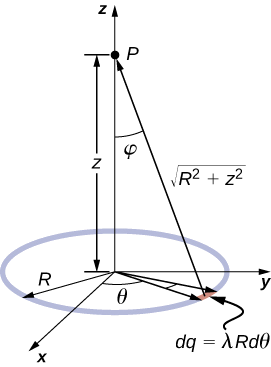
Oplossing
Het elektrisch veld voor een lijnlading wordt gegeven door de algemene uitdrukking
Een algemeen element van de boog tussen \theta en \theta + d\theta heeft lengte \(Rdtheta) en bevat dus een lading gelijk aan \lambda Rd\theta). Het element staat op een afstand van r = qrtz^2 + R^2 van P, de hoek is \cos \, \phi = \dfrac{z}{\sqrt{z^2+R^2}}) en dus is het elektrisch veld
&= \dfrac{1}{4\pi \epsilon_0} \dfrac{(z^2 + R^2)^{3/2}} \Wat{z} \int_0^{2\pi} d\theta \ &= \dfrac{1}{4\pi \epsilon_0} \dfrac{2}{(z^2 + R^2)^{3/2}} \Wat{z} &= \dfrac{1}{4}pi \epsilon_0} \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}} \Dat{z}.
Zoals gebruikelijk heeft de symmetrie dit probleem vereenvoudigd, in dit specifieke geval resulteert dit in een triviale integraal. Als we de limiet van z nemen, vinden we dat
zoals we verwachten.
Voorbeeld (\PageIndex{3B}\): Het veld van een schijf
Bepaal het elektrisch veld van een cirkelvormige dunne schijf met straal \(R\) en uniforme ladingsdichtheid op een afstand \(z\) boven het middelpunt van de schijf (figuur \(\PageIndex{4}})
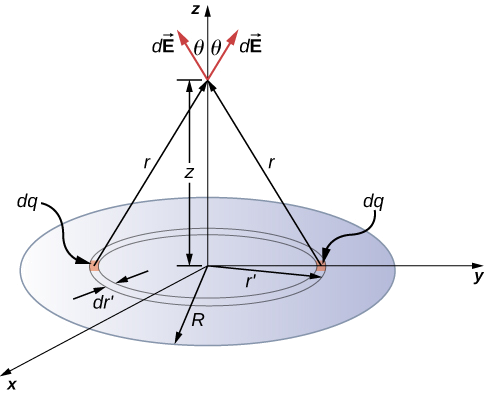
Strategie
Het elektrisch veld voor een oppervlaktelading wordt gegeven door
Om oppervlakteladingsproblemen op te lossen, breken we het oppervlak op in symmetrische differentiële “strepen” die overeenkomen met de vorm van het oppervlak; hier gebruiken we ringen, zoals in de figuur is aangegeven. Opnieuw, door symmetrie, heffen de horizontale componenten op en is het veld volledig in de verticale richting. De verticale component van het elektrisch veld wordt verkregen door vermenigvuldiging met (\theta}), dus
Zoals voorheen moeten we de onbekende factoren in de integrand herschrijven in termen van de gegeven grootheden. In dit geval
(Let op de twee verschillende “r’s” hier; r’s is de afstand van de differentiaalring van lading tot het punt waar we het veld willen bepalen, terwijl r’s de afstand van het middelpunt van de schijf tot de differentiaalring van lading is). Ook hebben we de poolhoekintegraal al uitgevoerd door \(dA\) op te schrijven.
Oplossing
Substitueren we dit alles in, dan krijgen we
&= \dfrac{1}{4 \pi \epsilon_0} \int_0^R \dfrac{(2)sigma(r’ dr’)z}{(r’^2 + z^2)^{3/2}} \hat{k} &= \dfrac{1}{4 \pi \epsilon_0} links(\dfrac{1}{z} – \dfrac{1}{sqrt{R^2 + z^2}} rechts) \hat{k} \eind{align*}]
of, eenvoudiger,
Belang
Ook hier kan worden aangetoond (via een Taylor-expansie) dat wanneer z \gg R\), dit reduceert tot
wat de uitdrukking is voor een puntlading \(Q = \sigma \pi R^2}).
PageIndex{3})
Hoe zou de bovenstaande limiet veranderen met een gelijkmatig geladen rechthoek in plaats van een schijf?
Antwoord
De puntlading wordt dan (Q = \sigma ab) waarbij \(a) en \(b) de zijden van de rechthoek zijn, maar verder identiek.
Als \(R) \rechthoekig \infty}), reduceert Vergelijking \ref{5.14} herleid tot het veld van een oneindig vlak, dat een vlak is waarvan de oppervlakte veel, veel groter is dan de dikte, en ook veel, veel groter dan de afstand waarop het veld moet worden berekend:
&= \dfrac{\sigma}{2 \epsilon_0} \hat{k}. {\label{5.15}
Merk op dat dit veld constant is. Dit verrassende resultaat is, alweer, een artefact van onze limiet, maar wel een die we in de toekomst nog vaak zullen gebruiken. Om te begrijpen waarom dit gebeurt, stel je voor dat je boven een oneindig vlak van constante lading staat. Ziet het vliegtuig er anders uit als je je hoogte varieert? Nee, je ziet het vliegtuig nog steeds naar oneindig gaan, hoe ver je er ook vanaf bent. Het is belangrijk op te merken dat vergelijking 5.15 is omdat we boven het vlak zijn. Als we eronder zouden zitten, zou het veld in de richting (- \dat{k}} wijzen.
Voorbeeld (\PageIndex{4}}): Het veld van twee oneindige vlakken
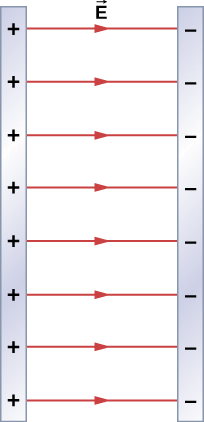
Ontdek overal het elektrisch veld als gevolg van twee oneindige vlakken met gelijke maar tegengestelde ladingsdichtheden (figuur \(\PageIndex{5})).
Strategie
We kennen al het elektrisch veld van een enkel oneindig vlak, dus kunnen we het principe van superpositie gebruiken om het veld van twee te vinden.
Oplossing
Het elektrisch veld wijst weg van het positief geladen vlak en naar het negatief geladen vlak. Omdat de velden gelijk en tegengesteld zijn, betekent dit dat in het gebied buiten de twee vlakken, de elektrische velden elkaar opheffen tot nul. Maar in het gebied tussen de vlakken tellen de elektrische velden op, en krijgen we
voor het elektrisch veld. Dat komt omdat in de figuur het veld in de +x-richting wijst.
Betekenis
Systemen die benaderd kunnen worden als twee oneindige vlakken van dit soort bieden een nuttige manier om uniforme elektrische velden te maken.
PageIndex{4})
Hoe zou het elektrisch veld eruit zien in een systeem met twee evenwijdige positief geladen vlakken met gelijke ladingsdichtheden?
Antwoord
Het elektrisch veld zou daartussen nul zijn, en verder overal een grootte hebben van (\dfrac{sigma}{epsilon_0}).
Bijdragers en toeschrijvingen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), en Bill Moebs met vele auteurs die een bijdrage hebben geleverd. Dit werk is gelicenseerd door OpenStax University Physics onder een Creative Commons Naamsvermelding Licentie (by 4.0).