Toon mobiele notitie Toon alle notities Verberg alle notities
Hoofdstuk 1-12 : Cilindrische Coördinaten
Zoals in de tweedimensionale ruimte wordt het standaard links( {x,y,z} rechts)-coördinatensysteem het cartesisch coördinatensysteem genoemd. In de laatste twee paragrafen van dit hoofdstuk bekijken we enkele alternatieve coördinatenstelsels voor de driedimensionale ruimte.
We beginnen met het cilindrische coördinatenstelsel. Dit is vrij eenvoudig omdat het niets meer is dan een uitbreiding van poolcoördinaten naar drie dimensies. Niet alleen is het een uitbreiding van poolcoördinaten, maar we breiden het uit naar de derde dimensie net zoals we Cartesische coördinaten uitbreiden naar de derde dimensie. Het enige wat we doen is er een derde coördinaat aan toevoegen. De r- en z-coördinaten zijn dezelfde als bij poolcoördinaten.
Hier volgt een schets van een punt in \({\mathbb{R}^3})
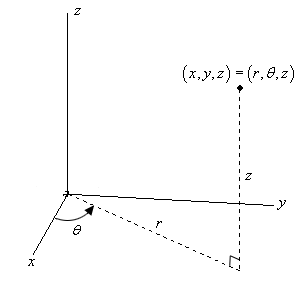
De omzettingen voor x(x) en y(y) zijn dezelfde omzettingen die we gebruikten toen we naar poolcoordinaten keken. Dus, als we een punt in cylindrische coördinaten hebben, dan kunnen we de cartesische coördinaten vinden door de volgende omzettingen te gebruiken.
De derde vergelijking is gewoon een erkenning dat de \(z\)-coördinaat van een punt in cartesische en polaire coördinaten hetzelfde is.
Ook als we een punt in cartesische coördinaten hebben, kunnen we de cilindrische coördinaten vinden met behulp van de volgende omzettingen.
Laten we eens snel kijken naar enkele oppervlakken in cilindrische coördinaten.
- (r = 5)
- ({r^2} + {z^2} = 100)
- (z = r)
Toon alle oplossingen Verberg alle oplossingen
In twee dimensies weten we dat dit een cirkel is met straal 5. Omdat we nu in drie dimensies zijn en er geen \(z) in de vergelijking staat, betekent dit dat deze vrij mag variëren. Dus voor elke gegeven straal hebben we een cirkel met straal 5 met het middelpunt op de z-as.
Met andere woorden, we hebben een cilinder met straal 5 met het middelpunt op de z-as.
b ²({r^2} + {z^2} = 100}) Toon oplossing
Deze vergelijking is gemakkelijk te achterhalen als we terugrekenen naar cartesische coördinaten.
Dus dit is een bol met het middelpunt in de oorsprong en een straal van 10.
c ²(z = r²) Toon oplossing
Ook deze is niet zo moeilijk als we terugrekenen naar cartesische coördinaten. Om redenen die uiteindelijk duidelijk zullen worden, kwadrateren we eerst beide zijden en rekenen dan om.
Uit het hoofdstuk over kwadratische oppervlakken weten we dat dit de vergelijking van een kegel is.