De Fouriertransformatie (FT) ontleedt een signaal in de frequenties waaruit het is opgebouwd.
Wat betekent dit?
Zo, laten we een voorbeeld nemen. Stel we hebben een signaal S1.

Als we de sterkte van dit signaal op een bepaald tijdstip willen meten.
Dus de amplitude van het signaal S1 is 1
Als we hetzelfde doen voor een ander signaal en hetzelfde moment in de tijd kiezen, meten we de amplitude ervan. Stel we hebben een ander signaal S2 zoals dit

Ook de amplitude van het signaal S2 is 2
Nu, wat gebeurt er als we deze twee signalen tegelijkertijd uitzenden (S1 en S2) ?
Dus, wanneer we deze twee signalen op hetzelfde moment uitzenden, krijgen we een nieuw signaal dat de som is van de amplitude van deze twee signalen. Dit is zo omdat deze twee signalen bij elkaar worden opgeteld.

Dus, de amplitude van S3 = amplitude van S1 + amplitude van S2 = 1 + 2 = 3
Dus de amplitude van signaal S3 is 3
Nu, de interessante vraag is :
Als we alleen signaal S3 krijgen (dat de som is van de signalen S1 en S2).Kunnen we dan de oorspronkelijke signalen S1 en S2 terugvinden?
Ja. Dat is wat een Fourier-transformatie doet. Het neemt een signaal en ontleedt het tot de frequenties waaruit het is opgebouwd.
In ons voorbeeld zou een Fourier-transformatie het signaal S3 ontleden in de samenstellende frequenties zoals de signalen S1 en S2
Maar, hoe kunnen we de oorspronkelijke signalen terugkrijgen? Wat zal de Fourier-transformatie voor ons doen ?

Let op de drie signalen in bovenstaande afbeelding: S1, S2 en S3 en wanneer we deze drie signalen samenvoegen, krijgen we het signaal in het rood, dat in feite de som is van de drie signalen S1+S2+S3.
Wat de Fourier-transformatie doet, is ons van het tijdsdomein naar het frequentiedomein verplaatsen.
In het geval, dat iemand zich afvraagt, wat als we van het frequentiedomein terug willen naar het tijdsdomein?
Dat kunnen we doen met behulp van Inverse Fourier-transformatie (IFT). Maar dat zullen we in dit artikel niet bespreken.
Signaalgeneratie en faseverschuiving
Als we een signaal willen beschrijven, hebben we drie dingen nodig :
- De frequentie van het signaal die aangeeft, hoeveel voorvallen in de periode die we hebben.
- Amplitude die de hoogte van het signaal aangeeft of in andere bewoordingen de sterkte van het signaal.
- Faseverschuiving die aangeeft waar het signaal begint.
Het allereerste voorbeeld dat we hebben genomen was heel eenvoudig, elk signaal had dezelfde frequentie en faseverschil en alleen verschillende amplitudes.
We gaan nu kijken naar een iets ingewikkelder voorbeeld en we gaan kijken naar het afzonderlijke signaal uit het bovenstaande voorbeeld, want om de Fourier-transformatie beter te begrijpen moeten we de afzonderlijke signalen goed bekijken.
Hieronder staan de oorspronkelijke signalen waarnaar we hierboven keken.



Frequentie: Als we goed naar de drie signalen kijken, zullen we merken dat de frequentie van alle drie de signalen verschillend is.
Als er voor dezelfde tijdsperiode in signaal 1 n aantal golven is, dan zijn er 2n aantal golven in signaal 2 en omgekeerd.
Fase: Ook, als we goed kijken naar waar het signaal eigenlijk begint. We zullen zien dat signaal 1 begint bij (0,0), terwijl signaal 2 begint bij (-0,5,0) als we de golf volgen om de y-as te ontmoeten bij 0. Dus, bij 0 hebben we al de maximale amplitude van het signaal. Dit is wat we faseverschuiving noemen.
Amplitude: Alle drie de signalen hebben verschillende amplitudes, Signaal 1 heeft een amplitude van 1 terwijl signaal 2 en signaal 3 een amplitude hebben van respectievelijk 2 en 3.
Dit alles is gevat in een elegante en super eenvoudige wiskundige formule. In de bovenstaande voorbeelden wordt de x-as x genoemd en de y-as y. We kunnen y genereren als een functie van t zodanig dat :

Met deze formule, kunnen we elk type signaal genereren dat we willen en dan kunnen we ze samenvoegen en ermee spelen. Bijvoorbeeld, als we de signalen 1, 2 en 3 samenvoegen. krijgen we een signaal als dit:

De wiskunde achter Fouriertransformatie
Het belangrijkste idee achter Fouriertransformatie is dat :
Elk continu signaal in het tijdsdomein kan uniek en eenduidig worden voorgesteld door een oneindige reeks sinusoïden.
Wat betekent dit?
Het betekent dat, als we een signaal hebben en dit signaal wordt opgewekt door een of andere functie x(t) dan kunnen we een andere functie f(t) bedenken zodanig dat :

Dus, Het maakt niet uit hoe sterk het signaal is, we kunnen een functie als f(t) vinden die een som is van een oneindige reeks sinusoïden die het signaal in feite perfect zal weergeven.
De vraag die nu rijst is, hoe vinden we de coëfficiënten hier in de bovenstaande vergelijking omdat dit de waarden zijn die de vorm van de output en dus het signaal zouden bepalen.
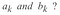
Dus, om deze coëfficiënten te krijgen gebruiken we Fouriertransformaties en het resultaat van Fouriertransformatie is een groep coëfficiënten. We gebruiken dus X(F) om de Fourier coëfficiënten aan te duiden en het is een functie van de frequentie die we krijgen door de integraal zo op te lossen dat :
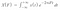
Het lastige deel in deze integraal is eigenlijk de i die een complex getal aanduidt. Dus, we herinneren ons waarschijnlijk dat i² = -1 of i = √-1. Het kan ook helpen om te onthouden dat de vorm van een complex getal a + ib is. Het heeft dus een reëel en een imaginair deel.
En als we de bovenstaande integraal oplossen, krijgen we deze complexe getallen waarbij a en b overeenkomen met de coëfficiënten waarnaar we op zoek zijn.
We hebben echter drie problemen die we moeten oplossen :
- Hoe gaan we om met
i. - Hoe om te gaan met discrete signalen.
Dus, laten we beginnen met de tweede.
Om de Discrete Fourier Transformatie te begrijpen, moeten we eerst begrijpen hoe je een continu signaal bemonstert?
Volgens Wikipedia, In signaalverwerking, is bemonstering de reductie van een continu-tijd signaal naar een discreet-tijd signaal. Hier is een voorbeeld van hoe de vorm van het signaal verandert met de verandering van de bemonsteringsfrequentie :
Laat het oorspronkelijke signaal een signaal zijn met een amplitude van twee en een frequentie van vijf over een periode van één seconde :
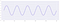
Nu, als we de bemonsteringsfrequentie verlagen, laten we eens kijken hoe de vorm van het signaal verandert :
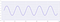
Als we de sampling rate verder verlagen, krijgen we :

Dus, waar het op neerkomt is : Hoe hoger de bemonsteringsfrequentie, hoe beter de kwaliteit van het signaal en we kunnen ook onderscheid maken tussen meer frequenties.
Nu we weten hoe we signalen moeten bemonsteren, zullen we kijken naar de wijziging van de algoritmen die bekend staat als Discrete Fourier Transformatie.
Discrete Fourier Transformatie
Elk bemonsterd signaal van lengte N in het tijdsdomein kan uniek en ondubbelzinnig worden voorgesteld door een eindige reeks sinusoïden.
Dus, we hebben in onze nieuwe definitie niet meer te maken met oneindigheid.
Wat is het verschil?
In de standaard Fourier Transformatie gebruikten we een functie van de tijd x(t) om een continu signaal op te wekken. In het discrete geval hebben we geen functie, we hebben een dataset, een set punten die we krijgen door het continue signaal te bemonsteren. Dus, ik zal {x} gebruiken om een dataset te doneren zodat het de lezing bevat van de bemonstering zodanig dat :

en wat de Discrete Fourier Transform voor ons zal doen is dat het de dataset van {x} zal transformeren in een andere dataset {X} die de Fourier coëfficiënten zal bevatten zodanig dat :

Als we kijken naar de definitie van Fourier Transform, is elke X in {X} een complex getal en bevat het de a en b componenten voor de frequenties.
Maar, hoe komt het dat de twee datasets {x} en {X} dezelfde lengte hebben?
Als we nadenken over, wat de lengte van {x} dataset drijft is de bemonsteringsfrequentie omdat, over een periode van tijd, het aantal datapunten dat ik lees precies de bemonsteringsfrequentie is, toch? Als we denken aan de andere dataset {X} , zeiden we dat frequentie het aantal voorvallen per tijdseenheid is. Dus als ik bemonster met een bepaalde frequentie, kan ik geen signalen herkennen die een hogere frequentie hebben dan de bemonsteringsfrequentie, gewoon omdat we niet genoeg datapunten krijgen.
Dus, als we signalen hebben met zeer hoge frequenties op een zeer lage bemonsteringsfrequentie, zullen we niet in staat zijn om deze signalen helemaal te herkennen. Het aantal frequenties dat we kunnen herkennen door de Fourier Transformatie toe te passen, wordt dus ook bepaald door de bemonsteringsfrequentie.
Dus, nu we onze dataset {x} hebben, krijgen we {Xk} zodanig dat het een element is in {X} die mijn Fourier coëfficiënten zijn zodanig dat :
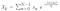
Dus, dit is in wezen de discrete fouriertransformatie. We kunnen deze berekening uitvoeren en het zal een complex getal opleveren in de vorm van a + ib waarbij we twee coëfficiënten hebben voor de Fourier-reeks.
Nu weten we hoe we signalen kunnen bemonsteren en hoe we een Discrete Fourier Transformatie kunnen toepassen. Het laatste wat we willen doen is, we willen ons ontdoen van het complexe getal i omdat het niet wordt ondersteund in mllib of systemML door iets te gebruiken dat bekend staat als de formule van Euler die stelt :
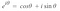
Dus, Als we de formule van Euler in de vergelijking van de Fourier Transformatie stoppen, krijgen we

we weten ook dat cos(-θ) = cos(θ) en sin(-θ) = -sin(θ) en als we dit gebruiken in de bovenstaande vergelijking, kan de vergelijking vereenvoudigd worden als :

en we kunnen de bovenstaande vergelijking eigenlijk in twee sommen breken zodanig dat :

Nu, Als we de bovenstaande vergelijking vergelijken met de vergelijking van een complex getal dat a + ib is, dan krijgen we de overeenkomstige waarde als :
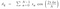
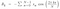
Dus, nu kunnen we deze waarden in de vergelijking van f(t) stoppen en het resultaat krijgen.
Conclusie
In de praktijk gebruiken we een kleine aanpassing van de discrete fouriertransformatie, de zogenaamde snelle fouriertransformatie, omdat de discrete fouriertransformatie zeer eenvoudig, elementair en traag is. Het is niet geschikt voor het doel als we echt iets willen doen in een produktie omgeving. Computation complexity of Discrete Fourier Transform is quadratic time O(n²) and Fast Fourier Transform for comparison is quasi-linear time O(nlogn). Fast Fourier Transform doet dit door gebruik te maken van assymetrie in de Fourier Transformatie.