Wat is gezamenlijke waarschijnlijkheid?
Gezamenlijke waarschijnlijkheid is een maat die wordt gevonden door de waarschijnlijkheid te berekenen dat twee gebeurtenissen tegelijk plaatsvinden. Met andere woorden, het is de kans dat gebeurtenis X op hetzelfde moment plaatsvindt als gebeurtenis Y, zoals een kruising van twee gebeurtenissen.
Gezamenlijke waarschijnlijkheid voor afhankelijke gebeurtenissen
Om de gezamenlijke waarschijnlijkheid te meten, moeten beide gebeurtenissen op hetzelfde moment plaatsvinden en moeten ze onafhankelijk van elkaar zijn. Dat betekent dat de gezamenlijke waarschijnlijkheid voor afhankelijke gebeurtenissen niet kan worden bepaald.
Stel dat je wilt bepalen of het gaat regenen op hetzelfde moment dat er wolken aan de hemel staan. Deze twee gebeurtenissen zijn van elkaar afhankelijk, want als het regent, zullen er hoogstwaarschijnlijk wolken zijn. Daarom zijn deze gebeurtenissen van elkaar afhankelijk.
In plaats van gezamenlijke waarschijnlijkheid moet voor afhankelijke gebeurtenissen voorwaardelijke waarschijnlijkheid worden gebruikt.
Gezamenlijke waarschijnlijkheid voor onafhankelijke gebeurtenissen
Zoals gezegd, om een gezamenlijke waarschijnlijkheid te bepalen, moeten beide gebeurtenissen onafhankelijk van elkaar zijn. Bijvoorbeeld, de kans op “munt” of “kop” bij het opgooien van een munt zijn onafhankelijke gebeurtenissen. Met andere woorden, de kans op een munt bij de eerste opgooi heeft geen invloed op de kans op kop als je de munt een tweede keer opgooit.
Hoe bereken je gezamenlijke kans
Wanneer je leert hoe je gezamenlijke kans berekent, is het cruciaal om te begrijpen dat de formule vereist dat de twee gebeurtenissen onafhankelijk van elkaar zijn. Dat betekent dat de uitkomst van de ene gebeurtenis de impact van de uitkomst van de andere gebeurtenis niet kan beïnvloeden. Voordat u de gezamenlijke waarschijnlijkheid berekent, moet u zich afvragen of de uitkomst van de ene gebeurtenis de uitkomst van de andere zal beïnvloeden.
Sinds gezamenlijke waarschijnlijkheid kan worden omschreven als “het snijpunt van twee gebeurtenissen”, zal de formule de twee – en hoe ze elkaar kunnen snijden – omvatten.
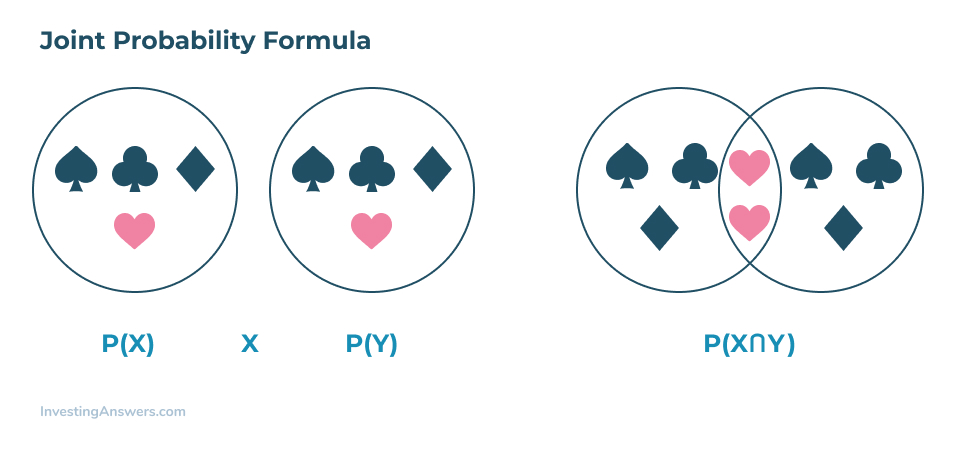
In de formule hieronder zie je het symbool “∩” gebruikt om een snijpunt aan te geven. Voor meer visuele leerlingen is het gebruik van een Venn-diagram de beste manier om te illustreren hoe twee gebeurtenissen elkaar kunnen snijden.
Gezamenlijke waarschijnlijkheidsformule
De gezamenlijke waarschijnlijkheidsformule is als volgt:
In deze formule stellen X en Y beide twee verschillende gebeurtenissen voor die elkaar snijden, en P is gelijk aan de samenvoegingskans van zowel X als Y.
Een andere manier om de gezamenlijke waarschijnlijkheidsformule uit te drukken is P( X en Y) en P(XY).
Voorbeeld gezamenlijke kans #1
Laten we zeggen dat je de gezamenlijke kans wilt berekenen voor een muntworp waarbij je een munt krijgt (gebeurtenis X) gevolgd door een muntkop (gebeurtenis Y).
In dit geval is de kans op gebeurtenis X 50% (of 0,5) en de kans op gebeurtenis Y is ook 50%. Nu kunnen we de getallen in de formule invoeren:
P(0.5 x 0.5) = 0.25 of 25%
Dat betekent dat de gezamenlijke kans op een muntstuk met een munt en een muntstuk met een kop 25% is.
Joint Probability Example #2
Je gooit met een dobbelsteen en je wilt de gezamenlijke kans bepalen dat je twee keer achter elkaar het getal zes gooit. De kans dat je de eerste keer een zes krijgt is 1/6, omdat er maar zes mogelijkheden zijn in een zeszijdige dobbelsteen. Dit komt overeen met ⅙, of 17% (in decimalen is dat 0,1666). Hetzelfde geldt als je de tweede keer een zes gooit.
Met deze informatie kunnen we bepalen dat de gezamenlijke kans dat je de eerste en de tweede keer een zes gooit het volgende is:
P(0,1666 x 0,1666) = 0,02777 of 2,8%
Dat betekent dat je 2,8% kans hebt dat beide gebeurtenissen plaatsvinden.
Wanneer gebruik je gezamenlijke kans
Gelijke kans is handig als je twee onafhankelijke gebeurtenissen wilt meten om te bepalen of ze gelijktijdig kunnen plaatsvinden.
Hoe wordt gezamenlijke waarschijnlijkheid gebruikt in relatie tot beleggen?
De gezamenlijke waarschijnlijkheid is een nuttige statistiek voor analisten en statistici wanneer twee of meer waarneembare verschijnselen gelijktijdig kunnen optreden. Bijvoorbeeld wanneer een daling van de Dow Jones Industrial Average gepaard gaat met een aanzienlijk waardeverlies van de dollar.
Je kunt ook twee afzonderlijke aandelen met elkaar vergelijken om te zien of de waarde van de ene stijgt (en of de andere dat ook doet).