“Graad” kan in de wiskunde verschillende dingen betekenen:
- In de Meetkunde is een graad (°) een manier om hoeken te meten,
- Maar hier bekijken we wat graad in de Algebra betekent.
In de Algebra wordt “Graad” soms “Orde” genoemd”
Graad van een polynoom (met één variabele)
Een polynoom ziet er zo uit:
voorbeeld van een polynoom
deze heeft 3 termen
De Graad (voor een polynoom met één variabele, zoals x) is:
de grootste exponent van die variabele.
Meer voorbeelden:
| 4x | De Graad is 1 (een variabele zonder een exponent heeft in feite een exponent van 1) |
|
| De Graad is 3 (grootste exponent van x) | ||
| x2 + 2×5 – x | De Graad is 5 (grootste exponent van x) | |
| De graad is 2 (grootste exponent van z) |
Namen van graden
Als we de graad weten, kunnen we er ook een naam aan geven!
| Degree | Name | Example |
|---|---|---|
| 0 | 7 | |
| 1 | Lineair | x+3 |
| 2 | x2-x+2 | |
| 3 | Kubisch | x3-x2+5 |
| 4 | kwartisch | 6x4x3+x-2 |
| 5 | Quintic | x5-3×3+x2+8 |
Voorbeeld: y = 2x + 7 heeft een graad van 1, dus het is een lineaire vergelijking
Voorbeeld: 5w2 – 3 heeft een graad van 2, dus is het een kwadratische vergelijking
Vergelijkingen van een hogere orde zijn meestal moeilijker op te lossen:
- Lineaire vergelijkingen zijn gemakkelijk op te lossen
- Quadratische vergelijkingen zijn iets moeilijker op te lossen
- Cubische vergelijkingen zijn weer moeilijker, maar er zijn formules om te helpen
- Quartische vergelijkingen kunnen ook worden opgelost, maar de formules zijn erg ingewikkeld
- Quintische vergelijkingen hebben geen formules, en kunnen soms onoplosbaar zijn!
Graad van een polynoom met meer dan één variabele
Wanneer een polynoom meer dan één variabele heeft, moeten we elke term bekijken. Termen worden gescheiden door + of – tekens:
voorbeeld van een polynoom
met meer dan één variabele
Voor elke term:
- Vind de graad door de exponenten van elke variabele erin op te tellen,
De grootste van die graden is de graad van de polynoom.
Voorbeeld: wat is de graad van deze polynoom:
Kijk elke term na:
- 5xy2 heeft een graad van 3 (x heeft een exponent van 1, y heeft 2, en 1+2=3)
- 3x heeft een graad van 1 (x heeft een exponent van 1)
- 5y3 heeft een graad van 3 (y heeft een exponent van 3)
- 3 heeft een graad van 0 (geen variabele)
De grootste graad van deze termen is 3 (in feite hebben twee termen een graad van 3), dus de polynoom heeft een graad van 3
Voorbeeld: wat is de graad van deze polynoom:
4z3 + 5y2z2 + 2yz
Kijk elke term na:
- 4z3 heeft een graad van 3 (z heeft een exponent van 3)
- 5y2z2 heeft een graad van 4 (y heeft een exponent van 2, z heeft 2, en 2+2=4)
- 2yz heeft een graad van 2 (y heeft een exponent van 1, z heeft 1, en 1+1=2)
De grootste graad daarvan is 4, dus de veelterm heeft een graad van 4
Het opschrijven
In plaats van te zeggen “de graad van (wat dan ook) is 3” schrijven we het als volgt:
Wanneer de uitdrukking een breuk is
We kunnen de graad van een rationale uitdrukking (een uitdrukking in de vorm van een breuk) berekenen door de graad van de top (teller) te nemen en de graad van de bodem (noemer) ervan af te trekken.
Hier volgen drie voorbeelden:
Andere soorten uitdrukkingen berekenen
Waarschuwing: Gevorderde ideeën in het verschiet!
We kunnen de graad van een uitdrukking soms berekenen door …
- de logaritme van de functie te delen door
- de logaritme van de variabele
… doe dat dan voor steeds grotere waarden, om te zien waar het antwoord “naartoe” gaat.
(Correcter is het om de limiet tot oneindig van ln(f(x))/ln(x) uit te rekenen, maar ik wil het hier eenvoudig houden).
|
Note: “ln” is de natuurlijke logaritme functie. |
 |
Hier is een voorbeeld:
Voorbeeld: Wat is de graad van (3 plus de vierkantswortel van x) ?
Laten we toenemende waarden van x proberen:
| x | ln( ) |
ln(x) | ln() / ln(x) |
|---|---|---|---|
| 2 | 1.48483 | 0.69315 | 2.1422 |
| 4 | 1.60944 | 1.38629 | 1.1610 |
| 10 | 1.81845 | 2.30259 | 0.7897 |
| 100 | 2.56495 | 4.60517 | 0.5570 |
| 1.000 | 3.54451 | 6.90776 | 0.5131 |
| 10.000 | 4.63473 | 9.21034 | 0.5032 |
| 100.000 | 5.76590 | 11.51293 | 0,5008 |
| 1.000.000 | 6.91075 | 13.81551 | 0.5002 |
Kijken we naar de tabel:
- als x groter wordt dan ln(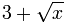) / ln(x) steeds dichter bij 0,5
Dus de Graad is 0.5 (met andere woorden 1/2)
(Opm: dit komt mooi overeen met x½ = vierkantswortel van x, zie Fractionele Exponenten)
Enkele Graadwaarden
| Expressie | Graad |
|---|---|
| log(x) | 0 |
| ex | ∞ |
| 1/x | -1 |
 |
1/2 |