Er zijn verschillende soorten singulariteiten, elk met verschillende fysische kenmerken die relevant zijn voor de theorieën waaruit ze oorspronkelijk zijn voortgekomen, zoals de verschillende vorm van de singulariteiten, kegelvormig en gekromd. Er is ook verondersteld dat ze voorkomen zonder Gebeurtenishorizonten, structuren die een ruimtetijdsectie afbakenen van een andere waarin gebeurtenissen voorbij de horizon niet kunnen ingrijpen; deze worden naakt genoemd.
Kegelvormige singulariteiten
Een kegelvormige singulariteit doet zich voor als er een punt is waar de limiet van elke diffeomorfisme invariante grootheid eindig is, in welk geval ruimtetijd niet glad is op het punt van de limiet zelf. De ruimtetijd ziet er dan uit als een kegel rond dit punt, waarbij de singulariteit zich op de top van de kegel bevindt. Overal waar het coördinatenstelsel wordt gebruikt kan de metriek eindig zijn.
Een voorbeeld van zo’n kegelsingulariteit is een kosmische snaar en een Schwarzschild zwart gat.
KrommingEdit
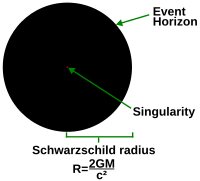
Oplossingen van de algemene relativiteitsvergelijkingen of een andere zwaartekrachtstheorie (zoals superzwaartekracht) leiden vaak tot punten waar de metriek tot oneindig wordt opgeblazen. Veel van deze punten zijn echter volkomen regelmatig, en de oneindigheden zijn slechts een gevolg van het gebruik van een ongeschikt coördinatenstelsel op dit punt. Om te testen of er een singulariteit is in een bepaald punt, moet men nagaan of in dit punt diffeomorfisme invariante grootheden (d.w.z. scalaren) oneindig worden. Zulke grootheden zijn in elk coördinatensysteem hetzelfde, dus deze oneindigheden zullen niet “weggaan” door een verandering van coördinaten.
Een voorbeeld is de Schwarzschild oplossing die een niet-roterend, ongeladen zwart gat beschrijft. In coördinatenstelsels die handig zijn om te werken in gebieden ver weg van het zwarte gat, wordt een deel van de metriek oneindig bij de waarnemingshorizon. De ruimtetijd aan de waarnemingshorizon is echter regelmatig. De regelmatigheid wordt duidelijk wanneer overgegaan wordt op een ander coördinatensysteem (zoals de Kruskal coördinaten), waar de metriek perfect glad is. Aan de andere kant, in het centrum van het zwarte gat, waar de metriek ook oneindig wordt, suggereren de oplossingen dat er een singulariteit bestaat. Het bestaan van de singulariteit kan worden geverifieerd door op te merken dat de Kretschmann scalar, zijnde het kwadraat van de Riemann tensor, d.w.z. R μ ν ρ σ R μ ν ρ σ {{\displaystyle R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }}

, die diffeomorfisme invariant is, is oneindig.
Terwijl in een niet-roterend zwart gat de singulariteit optreedt in een enkel punt in de modelcoördinaten, een “puntsingulariteit” genoemd, treedt in een roterend zwart gat, ook bekend als een Kerr zwart gat, de singulariteit op in een ring (een cirkelvormige lijn), een “ringsingulariteit” genoemd. Zo’n singulariteit kan theoretisch ook een wormgat worden.
Meer in het algemeen wordt een ruimtetijd als singulier beschouwd als hij geodetisch incompleet is, wat betekent dat er vrij vallende deeltjes zijn waarvan de beweging niet kan worden bepaald voorbij een eindige tijd, zijnde na het punt waarop de singulariteit wordt bereikt. Bijvoorbeeld, elke waarnemer binnen de waarnemingshorizon van een niet-roterend zwart gat zou binnen een eindige tijd in zijn centrum vallen. De klassieke versie van het Big Bang kosmologisch model van het heelal bevat een causale singulariteit aan het begin van de tijd (t=0), waar alle tijdachtige geodeten geen uitbreidingen naar het verleden hebben. Extrapolatie terug naar deze hypothetische tijd 0 resulteert in een heelal met alle ruimtelijke dimensies van grootte nul, oneindige dichtheid, oneindige temperatuur, en oneindige ruimtetijdkromming.
Naakte singulariteitEdit
Tot het begin van de jaren negentig werd algemeen aangenomen dat de algemene relativiteit elke singulariteit verbergt achter een waarnemingshorizon, waardoor naakte singulariteiten onmogelijk zijn. Dit wordt de kosmische censuurhypothese genoemd. In 1991 echter voerden de natuurkundigen Stuart Shapiro en Saul Teukolsky computersimulaties uit van een roterend stofvlak, waaruit bleek dat de algemene relativiteit “naakte” singulariteiten mogelijk zou kunnen maken. Hoe deze objecten er in een dergelijk model werkelijk uit zouden zien is onbekend. Evenmin is bekend of singulariteiten nog steeds zouden ontstaan als de vereenvoudigende aannames die voor de simulatie werden gebruikt, zouden worden weggelaten. Er wordt echter verondersteld dat licht dat een singulariteit binnenkomt, zijn geodetische lijnen op dezelfde manier zou beëindigen, waardoor de naakte singulariteit op een zwart gat zou lijken.
Zichtbare waarnemingshorizonten bestaan in de Kerr metriek, die een ronddraaiend zwart gat in vacuüm is, als het impulsmoment ( J {\displaystyle J}

) hoog genoeg is. Door de Kerr metriek om te zetten naar Boyer-Lindquist coördinaten kan worden aangetoond dat de coördinaat (die niet de straal is) van de waarnemingshorizon is, r ± = μ ± ( μ 2 – a 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-a^{2})^{1/2}}

, waarbij μ = G M / c 2 {\displaystyle \mu =GM/c^{2}}

, en a = J / M c {\displaystyle a=J/Mc}

. In dit geval betekent “waarnemingshorizonten verdwijnen” wanneer de oplossingen complex zijn voor r ± {\displaystyle r_{\pm }}

, of μ 2 < a 2 {{\displaystyle \mu ^{2}<a^{2}}

. Dit komt echter overeen met een geval waarin J {\displaystyle J}

groter is dan G M 2 / c {\displaystyle GM^{2}/c}

(of in Planck-eenheden, J > M 2 {\displaystyle J>M^{2}}

), d.w.z. de spin overschrijdt wat normaal wordt gezien als de bovengrens van zijn fysisch mogelijke waarden.
Ook met de Reissner-Nordström meetkunde van een geladen zwart gat zijn verdwijnende event horizons te zien als de lading ( Q {displaystyle Q}

) hoog genoeg is. In deze metriek kan worden aangetoond dat de singulariteiten optreden bij r ± = μ ± ( μ 2 – q 2 ) 1 / 2 {\displaystyle r_{\pm }= (\mu ^{2}-q^{2})^{1/2}}

, waarbij μ = G M / c 2 {\displaystyle r_{\pm }=mu \pm (\mu ^{2}-q^{2})^{1/2} , waarbij μ = G M / c 2 {\displaystyle \mu =GM/c^{2}}

, en q 2 = G Q 2 / ( 4 π ϵ 0 c 4 ) {\displaystyle q^{2}=GQ^{2}/(4 \pi \epsilon _{0}c^{4})}

. Van de drie mogelijke gevallen voor de relatieve waarden van μ {\displaystyle \mu}

en q {\displaystyle q}

, het geval waarin μ 2 < q 2 {\displaystyle \mu ^{2}<q^{2}}

veroorzaakt zowel r ± {\displaystyle r_{{2}}

complex zijn. Dit betekent dat de metriek regulier is voor alle positieve waarden van r {\displaystyle r}

, of met andere woorden, de singulariteit heeft geen waarnemingshorizon. Dit komt echter overeen met een geval waarin Q / 4 π ϵ 0 {\displaystyle Q/{\sqrt {4\pi \epsilon _{0}}}}

overschrijdt M G {\displaystyle M{\sqrt {G}}}

(of in Planck-eenheden, Q > M {\displaystyle Q>M}

), d.w.z. de lading overschrijdt wat normaal wordt gezien als de bovengrens van de fysisch mogelijke waarden. Ook van astrofysische zwarte gaten wordt niet verwacht dat ze een noemenswaardige lading bezitten.
Een zwart gat met de laagste M {{Displaystyle M}

waarde die overeenkomt met zijn J {\displaystyle J}

en Q {\displaystyle Q}

waarden en de hierboven genoemde grenzen, d.w.z. een waarde die net op het punt staat zijn waarnemingshorizon te verliezen, wordt extremaal genoemd.