
Logistische regressie werd in het begin van de twintigste eeuw gebruikt in de biologische wetenschappen. Daarna werd ze gebruikt in vele toepassingen in de sociale wetenschappen. Logistische regressie wordt gebruikt wanneer de afhankelijke variabele (doel) categorisch is.
Voorbeeld,
- Voorspellen of een e-mail spam is (1) of (0)
- Of de tumor kwaadaardig is (1) of niet (0)
Bedenk een scenario waarin we moeten classificeren of een e-mail spam is of niet. Als we voor dit probleem lineaire regressie gebruiken, moet er een drempelwaarde worden vastgesteld op basis waarvan de classificatie kan worden uitgevoerd. Stel dat de werkelijke klasse kwaadaardig is, de voorspelde continue waarde 0,4 en de drempelwaarde 0,5, dan zal het datapunt als niet kwaadaardig worden geclassificeerd, wat in real time tot ernstige gevolgen kan leiden.
Uit dit voorbeeld kan worden afgeleid dat lineaire regressie niet geschikt is voor een classificatieprobleem. Lineaire regressie is niet begrensd, en dit brengt logistische regressie in beeld. De waarde ervan varieert strikt van 0 tot 1.
Eenvoudige logistische regressie
(Volledige broncode: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Model
Uitgang = 0 of 1
Hypothese => Z = WX + B
hΘ(x) = sigmoïde (Z)
Sigmoïde Functie

Als ‘Z’ naar oneindig gaat, wordt Y(voorspeld) 1 en als ‘Z’ naar negatief oneindig gaat, wordt Y(voorspeld) 0.
Analyse van de hypothese
De output van de hypothese is de geschatte waarschijnlijkheid. Deze wordt gebruikt om af te leiden met hoeveel zekerheid de voorspelde waarde de werkelijke waarde kan zijn, gegeven de invoer X. Beschouw het onderstaande voorbeeld,
X = =
Op basis van de waarde x1, stellen we dat de geschatte waarschijnlijkheid 0,8 is. Dit betekent dat er 80% kans is dat een e-mail spam is.
Mathematisch kan dit worden geschreven als,

Dit rechtvaardigt de naam ‘logistische regressie’. De gegevens worden in een lineair regressiemodel ingepast, waarna een logistische functie de categorische afhankelijke doelvariabele voorspelt.
Typen logistische regressie
1. Binaire logistische regressie
De categorale respons heeft slechts twee mogelijke uitkomsten. Voorbeeld: Spam of Niet
2. Multinomiale logistische regressie
Drie of meer categorieën zonder volgorde. Voorbeeld: Voorspellen welk voedsel meer de voorkeur heeft (Veg, Niet-Veg, Vegan)
3. Ordinale Logistische Regressie
Drie of meer categorieën met ordening. Voorbeeld: Filmwaardering van 1 tot 5
Beslissingsgrens
Om te voorspellen tot welke klasse een gegeven behoort, kan een drempel worden ingesteld. Op basis van deze drempel wordt de verkregen geschatte waarschijnlijkheid in klassen ingedeeld.
Zeg, als voorspelde_waarde ≥ 0,5, dan classificeer e-mail als spam anders als geen spam.
De beslissingsgrens kan lineair of niet-lineair zijn. De polynomiale orde kan worden verhoogd om een complexe beslissingsgrens te krijgen.
Kostenfunctie
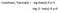
Waarom kan de kostenfunctie die voor lineaire regressie is gebruikt, niet worden gebruikt voor logistische regressie?
Lineaire regressie gebruikt de gemiddelde gekwadrateerde fout als kostenfunctie. Als deze wordt gebruikt voor logistische regressie, dan wordt het een niet-convexe functie van parameters (theta). Gradient descent convergeert alleen naar een globaal minimum als de functie convex is.

Kostenfunctie uitleg


Versimpelde kostenfunctie

Waarom deze kostenfunctie?
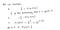
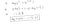
Deze negatieve functie is omdat we, wanneer we trainen, de waarschijnlijkheid moeten maximaliseren door de verliesfunctie te minimaliseren. Door de kosten te verlagen, neemt de maximale waarschijnlijkheid toe, ervan uitgaande dat de monsters uit een identiek onafhankelijke verdeling worden getrokken.
Het afleiden van de formule voor het Gradient Descent Algoritme


Python-implementatie
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Cost vs Number_of_Iterations

Train- en testnauwkeurigheid van het systeem is 100 %
Deze implementatie is voor binaire logistische regressie. Voor data met meer dan 2 klassen moet softmax regressie worden gebruikt.
Dit is een educatieve post en geïnspireerd op de deep learning cursus van Prof. Andrew Ng.
Volledige code : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb