
In een eerder artikel hebben we de lineaire regressieanalyse en de toepassing ervan in financiële analyse en modellering onderzocht. U kunt ons artikel over Regressieanalyse in financiële modellering lezen om meer inzicht te krijgen in de statistische concepten die in de methode worden gebruikt en waar deze wordt toegepast binnen de financiële wereld.
Dit artikel zal een praktische blik werpen op het modelleren van een Meervoudig Regressiemodel voor het Bruto Binnenlands Product (BBP) van een land.
Voordat ik begin, wil ik een korte disclaimer toevoegen. Ik ben geen statisticus, en ik beweer niet dat de gekozen afhankelijke en onafhankelijke variabelen de juiste analysekeuzes zijn. Het artikel is bedoeld om u te laten zien hoe u meervoudige regressie in Excel uitvoert en de output interpreteert, niet om u te leren hoe u onze modelaannames opstelt en de meest geschikte variabelen kiest.
Nu we dit uit de weg hebben en de verwachtingen zijn vastgesteld, laten we Excel openen en aan de slag gaan.
Wij halen voor deze exercitie openbare gegevens uit Eurostat, de statistische database van de Europese Commissie. Alle relevante brongegevens zijn voor uw gemak opgenomen in het modelbestand, dat u hieronder kunt downloaden. Ik heb ook de links naar de brontabellen bewaard, zodat u die desgewenst verder kunt onderzoeken.
De EU-dataset geeft ons informatie voor alle lidstaten van de Unie. Als grote fan van Agatha Christie’s Hercule Poirot, richten we onze aandacht op België.
Zoals u in de tabel hieronder kunt zien, hebben we negentien waarnemingen van onze doelvariabele (BBP), evenals onze drie voorspellende variabelen:
- X1 – Onderwijsuitgaven in mln.
- X2 – Werkloosheidspercentage als % van de beroepsbevolking;
- X3 – Beloning van werknemers in milj.

Nog voordat we ons regressiemodel hebben uitgevoerd, zien we een aantal afhankelijkheden in onze gegevens. Als we naar de ontwikkeling over de perioden kijken, kunnen we aannemen dat het BBP samen met de uitgaven aan onderwijs en de beloning van werknemers toeneemt.
Een meervoudige lineaire regressie uitvoeren
Er zijn manieren om alle relevante statistieken in Excel te berekenen met behulp van formules. Maar het is veel eenvoudiger met het hulppakket Gegevensanalyse, dat u kunt inschakelen vanaf het tabblad Ontwikkelaar -> Excel invoegtoepassingen.
Kijk naar het tabblad Gegevens, en aan de rechterkant ziet u het hulpprogramma Gegevensanalyse binnen het gedeelte Analyseren.
Uitvoeren en kies Regressie uit alle opties. Merk op dat we hetzelfde menu gebruiken voor zowel eenvoudige (enkelvoudige) als meervoudige lineaire regressiemodellen.
Nu is het tijd om enkele bereiken en instellingen in te stellen.
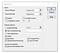
Het Y-bereik zal onze afhankelijke variabele, het BBP, bevatten. En in het X-bereik selecteren we alle kolommen van de X-variabele. Merk op dat dit hetzelfde is als het uitvoeren van een enkele lineaire regressie, met als enige verschil dat we meerdere kolommen kiezen voor het X-bereik.
Bedenk dat Excel vereist dat alle X-variabelen in aangrenzende kolommen staan.
Zoals ik de kolom Titels heb geselecteerd, is het van cruciaal belang het selectievakje voor Labels aan te vinken. Een betrouwbaarheidsinterval van 95% is geschikt in de meeste financiële analysescenario’s, dus we zullen dit niet veranderen.
U kunt vervolgens overwegen de gegevens op hetzelfde blad of een nieuw blad te plaatsen. Een nieuw werkblad werkt meestal het beste, omdat de tool nogal wat gegevens invoegt.
Ik zal ook alle extra opties onderaan aanvinken. Ik gebruik ze uiteindelijk zelden allemaal, maar het is gemakkelijker om de opties die we niet nodig hebben te verwijderen dan alles opnieuw te doen.
Teken in op onze nieuwsbrief voor een GRATIS Excel Benchmark Analyse Sjabloon
Evaluatie van de regressieresultaten
Nu we onze samenvattende output van Excel hebben, gaan we ons regressiemodel verder onderzoeken.
De informatie die wij uit de gegevensanalysemodule van Excel hebben gehaald, begint met de regressiestatistieken.
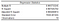
R-kwadraat is het belangrijkst van allemaal, dus we kunnen beginnen met er naar te kijken. In ons geval moeten we met name kijken naar het aangepaste R-kwadraat, omdat we meer dan één X-variabele hebben. Het geeft ons een idee van de algemene goedheid van de fit.
Een adjusted R Square van 0,98 betekent dat ons regressiemodel ongeveer 98% van de variatie van de afhankelijke variabele Y (BBP) rond de gemiddelde waarde van de waarnemingen (het gemiddelde van onze steekproef) kan verklaren. Met andere woorden, 98% van de variabiliteit in ŷ (y-hat, onze afhankelijke variabele voorspellingen) wordt door ons model opgevangen. Zo’n hoge waarde zou er gewoonlijk op wijzen dat er een probleem zou kunnen zijn met ons model. We gaan door met ons model, maar een te hoge R kwadraat kan problematisch zijn in een real-life scenario. Ik stel voor dat je dit artikel over Statistiek van Jim leest, om te leren waarom te goed niet altijd goed is in termen van R kwadraat.
De Standaardafwijking geeft ons een schatting van de standaardafwijking van de fout (residuen). In het algemeen geldt dat als de coëfficiënt groot is in vergelijking met de standaardfout, deze waarschijnlijk statistisch significant is.
Analysis of Variance (ANOVA)

Het gedeelte Analyse van variantie is iets dat we vaak overslaan bij het modelleren van regressie. Het kan echter waardevolle inzichten opleveren, en het is de moeite waard om er eens naar te kijken. U kunt meer lezen over het uitvoeren van een ANOVA-test en een voorbeeldmodel bekijken in ons speciale artikel.
Deze tabel geeft ons een algemene significantietest voor de regressieparameters.
De F-kolom van de ANOVA-tabel geeft ons de algemene F-test voor de nulhypothese dat alle coëfficiënten gelijk zijn aan nul. De alternatieve hypothese is dat ten minste een van de coëfficiënten niet gelijk is aan nul. De kolom Significantie F toont ons de p-waarde voor de F-test. Aangezien deze lager is dan het significantieniveau van 0,05 (bij het door ons gekozen betrouwbaarheidsniveau van 95%), kunnen wij de nulhypothese, dat alle coëfficiënten gelijk zijn aan nul, verwerpen. Dit betekent dat onze regressieparameters gezamenlijk niet statistisch insignificant zijn.
U kunt meer lezen over hypothesetoetsing in ons speciale artikel.
De volgende tabel geeft ons informatie over de coëfficiënten in ons Meervoudige Regressiemodel en is het spannendste deel van de analyse.

Hier hebben we veel details voor de intercept en elk van onze voorspellers (onafhankelijke variabelen). Laten we eens kijken wat deze kolommen voorstellen:
- Coefficiënten – dit zijn schattingen die zijn afgeleid met de kleinste-kwadratenmethode;
- Standaardfout – de standaardafwijking van de kleinste-kwadratenramingen;
- T-Stat – dit is de t-statistiek voor de nulhypothese dat de coëfficiënt gelijk is aan nul, versus de alternatieve hypothese dat deze verschillend is van nul;
- De P-waarde voor de t-test;
- Lager en Hoger 95% definiëren het betrouwbaarheidsinterval voor de coëfficiënten.
Test van statistische significantie
Dit is de toets van een nulhypothese die stelt dat de coëfficiënt een helling van nul heeft. We kunnen de p-waarden voor elke coëfficiënt bekijken en ze vergelijken met het significantieniveau van 0,05.
Als onze p-waarde lager is dan het significantieniveau, betekent dit dat onze onafhankelijke variabele statistisch significant is voor het model. Als we kijken naar onze voorspellers X1 tot X3, zien we dat alleen X3 Employee Compensation een p-waarde heeft van minder dan 0,05, wat betekent dat X1 Education Spend en X2 Unemployment Rate niet statistisch significant lijken te zijn voor ons regressiemodel.
Aangezien we de nulhypothese (dat de coëfficiënten gelijk zijn aan nul) niet kunnen verwerpen, kunnen we X1 en X2 uit het model elimineren. We kunnen dit ook bevestigen omdat de waarde nul tussen de onderste en bovenste betrouwbaarheidsintervallen ligt.
We kunnen besluiten het model uit te voeren zonder de variabelen X1 en X2 en te evalueren of dit leidt tot een significante daling van de aangepaste R-kwadraatmaat. Als dat niet het geval is, kunnen X1 en X2 veilig uit het regressiemodel worden verwijderd.
Als we dat doen, krijgen we de volgende regressiestatistieken.

We zien geen daling van het R-kwadraat, dus we kunnen X1 en X2 veilig uit ons model verwijderen en het vereenvoudigen tot een enkele lineaire regressie.
Residuele output
De residuen geven informatie over hoe ver de werkelijke gegevenspunten (y) afwijken van de voorspelde gegevenspunten (ŷ), gebaseerd op ons regressiemodel.

Kansberekening
Deze tabel toont de waargenomen waarden voor de onafhankelijke variabele (y) en de bijbehorende steekproefpercentielen. We kunnen het eerste percentiel berekenen als (100 / 2 * Aantal waarnemingen), en van daaruit worden deze berekend als het vorige percentiel + (100 / 2).

Residuplots
De meervoudige regressieanalyse geeft ons een plot voor elke onafhankelijke variabele versus de residuen. We kunnen deze plots gebruiken om te evalueren of onze steekproefgegevens voldoen aan de aannames voor lineariteit en homogeniteit.
Homogeniteit betekent dat de plot een willekeurig patroon moet vertonen en een constante verticale spreiding moet hebben.
Lineariteit vereist dat de residuen een gemiddelde van nul hebben. We kunnen dit visueel waarnemen door te beoordelen of de punten ongeveer gelijk verdeeld zijn onder en boven de x-as.



Line Fit Plots
Het model geeft ons een Line Fit Plot voor elke onafhankelijke variabele (voorspeller). Deze toont de voorspelde waarden (ŷ) tegenover de waargenomen waarden (y). Hoe beter deze overeenkomen, hoe beter ons model de afhankelijke variabele voorspelt op basis van de regressoren.



Normale waarschijnlijkheidsplot
De normale waarschijnlijkheidsplot helpt ons bepalen of de gegevens in een normale verdeling passen. We kunnen een Trendline toevoegen en evalueren of de datapunten een rechte lijn volgen. In ons geval ligt dat voor de hand, en voegen we de trendlijn misschien niet eens toe.

U kunt het voorbeeldmodel in Excel downloaden in het oorspronkelijke artikel.
Excel-beperkingen
Aangezien Excel geen gespecialiseerde statisticus-software is, zijn er enkele inherente beperkingen bij het uitvoeren van een regressiemodel waar we ons bewust van moeten zijn:
- Kolommen voor alle regressoren (onafhankelijke variabelen) moeten aangrenzend zijn;
- We kunnen maximaal 16 voorspellers hebben (ik weet niet meer waar ik dat gelezen heb, dus neem het met de nodige voorzichtigheid);
- De regressieanalyse in Excel gaat ervan uit dat de fout onafhankelijk is met constante variantie (homoskedasticiteit);
- Als we de functies route gaan, is het cruciaal om te weten dat Excel functies SLOPE, INTERCEPT, en FORECAST niet werken voor Meervoudige Regressie. TREND en LINEST daarentegen werken op dezelfde manier als bij een enkelvoudig regressiemodel, maar nemen waarden voor meerdere X-variabelen.
Conclusie
We begonnen met drie onafhankelijke variabelen, voerden een regressieanalyse uit, en stelden vast dat twee voorspellers geen statistische significantie voor ons model hebben.
Die hebben we vervolgens geëlimineerd om uit te komen op een Enkelvoudig Lineair Regressiemodel.
Als u tevreden bent met uw model, kunt u uw regressievergelijking opstellen, zoals we in andere artikelen hebben besproken. Met deze vergelijking kunt u dan de afhankelijke variabele voor de toekomst voorspellen.
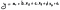
Waar:
- y is onze afhankelijke variabele;
- a is het intercept (onze constante) uit de regressiestatistiek;
- b, c, en d zijn de coëfficiënten voor elke variabele;
- x1 tot x3 zijn de onafhankelijke variabelen (onze regressoren of voorspellers);
- ɛ is de fout of residuen, die we vaak kunnen uitsluiten.
Houd in gedachten dat dit artikel is bedoeld om de concepten van het uitvoeren van een Meervoudige Regressie Analyse in Excel te illustreren. Het probeert uit te leggen waar we ons op moeten richten bij het evalueren van de resultaten. Elk goed model begint met het vaststellen van redelijke aannames en verwachtingen, waar ik geen expert in ben, dus ik beweer niet dat de gekozen afhankelijke en onafhankelijke variabelen de juiste keuzes waren.
Dank je voor het lezen! U kunt uw steun betuigen door dit artikel te delen met collega’s en vrienden.