- Behavior of the Sample Mean (x-bar)
- The Sampling Distribution of the Sample Mean
Gedrag van het steekproefgemiddelde (x-bar)
Tot nu toe hebben we het gedrag van de statistiek p-hat, de steekproefverhouding, ten opzichte van de parameter p, de populatieverhouding, besproken (wanneer de variabele van belang categorisch is).
We gaan nu verder met het onderzoeken van het gedrag van de statistiek x-bar, het steekproefgemiddelde, ten opzichte van de parameter μ (mu), het populatiegemiddelde (wanneer de variabele van belang kwantitatief is).
Laten we beginnen met een voorbeeld.
VOORBEELD 9: Gedrag van steekproefgemiddelden
Boortegewichten zijn geregistreerd voor alle baby’s in een stad. Het gemiddelde geboortegewicht is 3.500 gram, µ = mu = 3.500 g. Als we veel aselecte steekproeven nemen van 9 baby’s tegelijk, hoe zullen de steekproefgemiddelden zich dan gedragen?
Ook hier werken we met een toevalsvariabele, omdat aselecte steekproeven gemiddelden zullen hebben die op korte termijn onvoorspelbaar variëren, maar op lange termijn patronen vertonen.
Gebaseerd op onze intuïtie en wat we hebben geleerd over het gedrag van steekproefverhoudingen, kunnen we het volgende verwachten over de verdeling van steekproefmiddelen:
Centrum: Sommige steekproefgemiddelden zullen aan de lage kant zijn – zeg 3.000 gram of zo – terwijl andere aan de hoge kant zullen zijn – zeg 4.000 gram of zo. Bij herhaalde bemonstering mogen we verwachten dat de willekeurige steekproeven gemiddeld uitkomen op het onderliggende populatiegemiddelde van 3.500 g. Met andere woorden, het gemiddelde van de steekproefgemiddelden zal µ (mu) zijn, net zoals het gemiddelde van de steekproefproporties p was.
Spreiding: Voor grote steekproeven mogen we verwachten dat de steekproefgemiddelden niet te ver van het populatiegemiddelde van 3.500 zullen afwijken. Steekproefgemiddelden lager dan 3.000 of hoger dan 4.000 kunnen verrassend zijn. Voor kleinere steekproeven zouden we minder verrast zijn door steekproefgemiddelden die nogal van 3.500 afwijken. Met andere woorden, bij kleinere steekproeven zouden we een grotere variabiliteit in steekproefgemiddelden kunnen verwachten. De steekproefgrootte zal dus weer een rol spelen bij de spreiding van de verdeling van de steekproefmaten, zoals we ook bij de steekproefverhoudingen hebben gezien.
Vorm: Steekproefgemiddelden die het dichtst bij 3.500 liggen, zullen het meest voorkomen, terwijl steekproefgemiddelden die in beide richtingen ver van 3.500 liggen, geleidelijk minder waarschijnlijk worden. Met andere woorden, de vorm van de verdeling van de steekproefgemiddelden moet in het midden uitpuilen en aan de uiteinden taps toelopen met een vorm die enigszins normaal is. Dit is opnieuw wat we zagen toen we naar de steekproefverhoudingen keken.
Commentaar:
- De verdeling van de waarden van het steekproefgemiddelde (x-bar) bij herhaalde steekproeven wordt de steekproefverdeling van x-bar genoemd.
Laten we eens kijken naar een simulatie:
De resultaten die we in onze simulaties vonden, zijn niet verrassend. Geavanceerde kansrekening bevestigt dat door het volgende te beweren:
De steekproefverdeling van het steekproefgemiddelde
Als herhaalde aselecte steekproeven van een gegeven grootte n worden genomen uit een populatie van waarden voor een kwantitatieve variabele, waarbij het populatiegemiddelde μ (mu) is en de populatiestandaardafwijking σ (sigma), dan is het gemiddelde van alle steekproefgemiddelden (x-barren) populatiegemiddelde μ (mu).
Wat de spreiding van alle steekproefgemiddelden betreft, de theorie dicteert het gedrag veel preciezer dan te zeggen dat er minder spreiding is voor grotere steekproeven. In feite is de standaardafwijking van alle steekproefgemiddelden direct gerelateerd aan de steekproefgrootte, n, zoals hieronder is aangegeven.
![]()
Omdat de vierkantswortel van steekproefgrootte n in de noemer voorkomt, neemt de standaardafwijking inderdaad af naarmate de steekproefgrootte toeneemt.
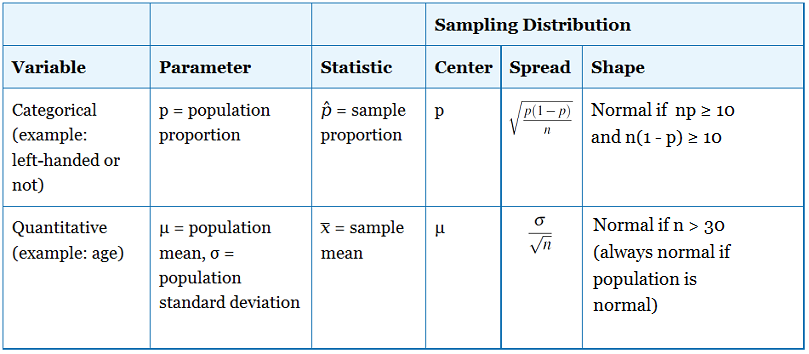
Laten we eens vergelijken en contrasteren wat we nu weten over de steekproefverdelingen voor steekproefgemiddelden en steekproefproporties.

Nu gaan we onderzoeken wat de vorm is van de steekproefverdeling van steekproefgemiddelden. Toen we de steekproefverdeling van steekproefproporties bespraken, zeiden we dat deze verdeling bij benadering normaal is als np ≥ 10 en n(1 – p) ≥ 10. Met andere woorden, we hadden een richtlijn op basis van steekproefgrootte voor het bepalen van de voorwaarden waaronder we normale kansberekeningen konden gebruiken voor steekproefverhoudingen.
Wanneer zal de verdeling van steekproefgemiddelden ongeveer normaal zijn? Hangt dit af van de grootte van de steekproef?
Het lijkt redelijk dat een populatie met een normale verdeling steekproefgemiddelden zal hebben die normaal verdeeld zijn, zelfs voor zeer kleine steekproeven. We zagen dit geïllustreerd in de vorige simulatie met steekproeven van grootte 10.
Wat gebeurt er als de verdeling van de variabele in de populatie sterk scheef is? Hebben steekproefgemiddelden ook een scheve verdeling? Als we echt grote steekproeven nemen, worden de steekproefgemiddelden dan meer normaal verdeeld?
In de volgende simulatie zullen we deze vragen onderzoeken.
Om samen te vatten: de verdeling van steekproefgemiddelden zal bij benadering normaal zijn, zolang de steekproefgrootte groot genoeg is. Deze ontdekking is waarschijnlijk het belangrijkste resultaat dat in inleidende cursussen statistiek wordt gepresenteerd. Het is formeel geformuleerd als de Central Limit Theorem.
We zullen steeds weer op de Central Limit Theorem terugvallen om normale kansberekeningen uit te voeren wanneer we steekproefgemiddelden gebruiken om conclusies te trekken over een populatiegemiddelde. We weten nu dat we dit zelfs kunnen doen als de populatieverdeling niet normaal is.
Hoe groot moet de steekproefomvang zijn om aan te nemen dat steekproefgemiddelden normaal verdeeld zijn? Nou, dat hangt echt af van de verdeling van de populatie, zoals we in de simulatie hebben gezien. De algemene vuistregel is dat steekproeven met een grootte van 30 of meer een tamelijk normale verdeling zullen hebben, ongeacht de vorm van de verdeling van de variabele in de populatie.
Commentaar:
- Voor categorische variabelen is onze bewering dat steekproefproporties bij benadering normaal zijn voor groot genoeg n eigenlijk een speciaal geval van de Central Limit Theorem. In dit geval beschouwen we de gegevens als 0’s en 1’s en is het “gemiddelde” van deze 0’s en 1’s gelijk aan de verhouding die we hebben besproken.
Voordat we met enkele voorbeelden aan de slag gaan, vergelijken en contrasteren we eerst wat we nu weten over de steekproefverdelingen voor steekproefgemiddelden en steekproefproporties.
VoorBEELD 10: Gebruik maken van de steekproefverdeling van x-bar
De grootte van het huishouden in de Verenigde Staten heeft een gemiddelde van 2,6 personen en een standaardafwijking van 1,4 personen. Het moet duidelijk zijn dat deze verdeling rechts scheef is, want de kleinst mogelijke waarde is een huishouden van 1 persoon, maar de grootste huishoudens kunnen zeer groot zijn.
(a) Wat is de kans dat een willekeurig gekozen huishouden meer dan 3 personen telt?
Een normale benadering mag hier niet worden gebruikt, want dan zou de verdeling van de grootte van huishoudens sterk naar rechts scheef zijn. We hebben niet genoeg informatie om dit probleem op te lossen.
(b) Wat is de kans dat de gemiddelde grootte van een aselecte steekproef van 10 huishoudens groter is dan 3?
Naar ieders maatstaven is 10 een kleine steekproefgrootte. De Central Limit Theorem garandeert niet dat steekproefgemiddelden uit een scheve populatie bij benadering normaal zijn, tenzij de steekproefgrootte groot is.
(c) Wat is de kans dat de gemiddelde grootte van een aselecte steekproef van 100 huishoudens groter is dan 3?
Nu kunnen we ons beroepen op de Central Limit Theorem: ook al is de verdeling van huishoudgrootte X scheef, de verdeling van de steekproefgemiddelde huishoudgrootte (x-bar) is bij benadering normaal voor een grote steekproefgrootte zoals 100. Het gemiddelde is gelijk aan het populatiegemiddelde, 2.6, en de standaardafwijking is de standaardafwijking van de populatie gedeeld door de vierkantswortel van de steekproefgrootte:

Om
te vinden
![]()
we standaardiseren 3 tot een z-score door het gemiddelde ervan af te trekken en het resultaat te delen door de standaardafwijking (van het steekproefgemiddelde). Vervolgens kunnen we de kans vinden met behulp van de standaard normale rekenmachine of tabel.

Huishoudens van meer dan 3 personen komen natuurlijk vrij vaak voor, maar het zou uiterst ongebruikelijk zijn als de gemiddelde grootte van een steekproef van 100 huishoudens meer dan 3 zou zijn.
Het doel van de volgende activiteit is om onder begeleiding te oefenen met het vinden van de steekproefverdeling van het steekproefgemiddelde (x-bar), en deze te gebruiken om te leren over de waarschijnlijkheid van het krijgen van bepaalde waarden van x-bar.