Je vraagt je misschien af wat al die sommen van kwadraten allemaal inhouden. Misschien ben je daarom hier terechtgekomen. Wel, het zijn de determinanten van een goede lineaire regressie. Deze handleiding is gebaseerd op het ANOVA-raamwerk dat je misschien al eerder hebt gehoord.
Voordat je dit leest, moet je er echter voor zorgen dat je regressie niet verwart met correlatie. Als je dit hebt gecontroleerd, kunnen we meteen aan de slag.
Een korte kanttekening: wil je meer leren over lineaire regressie? Bekijk dan onze uitlegvideo’s The Linear Regression Model. Geometrical Representation and The Simple Linear Regression Model.
SST, SSR, SSE: Definition and Formulas
Er zijn drie termen die we moeten definiëren. De som van de kwadraten totaal, de som van de kwadraten regressie, en de som van de kwadraten fout.

Wat is de SST?
De som van de kwadraten totaal, aangeduid met SST, is het gekwadrateerde verschil tussen de waargenomen afhankelijke variabele en zijn gemiddelde. Je kunt dit zien als de spreiding van de waargenomen variabelen rond het gemiddelde – ongeveer zoals de variantie in beschrijvende statistieken.
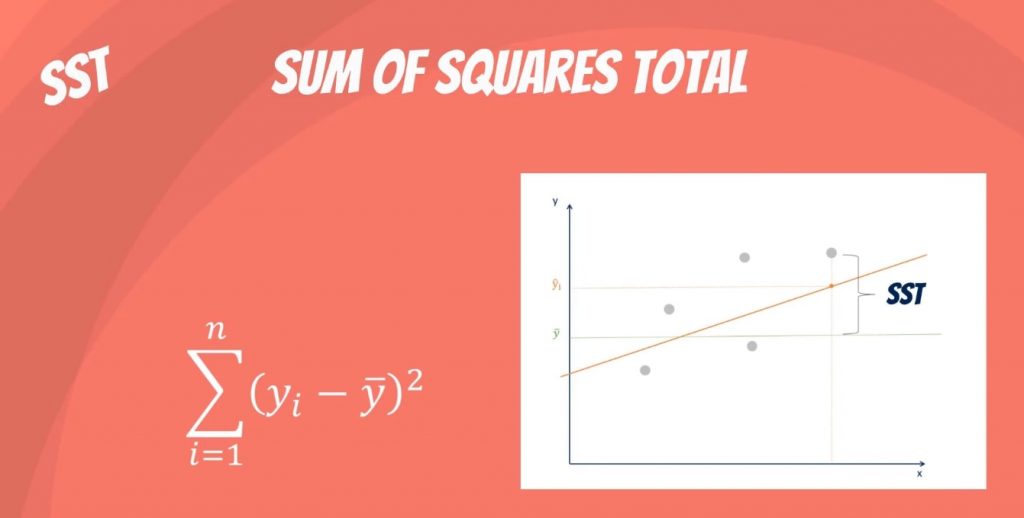
Het is een maat voor de totale variabiliteit van de dataset.
Noot terzijde: Er is een andere notatie voor de SST. Het is TSS of totale som van kwadraten.
Wat is de SSR?
De tweede term is de som van de kwadraten als gevolg van regressie, of SSR. Het is de som van de verschillen tussen de voorspelde waarde en het gemiddelde van de afhankelijke variabele. Zie het als een maatstaf die beschrijft hoe goed onze lijn bij de gegevens past.

Als deze waarde van SSR gelijk is aan de som van de kwadraten, betekent dit dat ons regressiemodel alle waargenomen variabiliteit vangt en perfect is. Nogmaals, een andere gebruikelijke notatie is ESS of verklaarde som van de kwadraten.
Wat is de SSE?
De laatste term is de som van de kwadraten fout, of SSE. De fout is het verschil tussen de waargenomen waarde en de voorspelde waarde.

Wij willen de fout meestal minimaliseren. Hoe kleiner de fout, hoe beter het schattingsvermogen van de regressie. Tot slot moet ik hieraan toevoegen dat het ook bekend staat als RSS of residuele som van kwadraten. Residueel als in: overgebleven of onverklaard.
De verwarring tussen de verschillende afkortingen
Het wordt echt verwarrend omdat sommige mensen het aanduiden als SSR. Daardoor is het onduidelijk of we het hebben over de som van de kwadraten als gevolg van regressie of over de som van de gekwadrateerde residuen.

In elk geval is geen van beide universeel gangbaar, dus de verwarring blijft bestaan en we zullen ermee moeten leven.
Bedenk gewoon dat de twee notaties SST, SSR, SSE zijn, of TSS, ESS, RSS.

Er is een conflict over de afkortingen, maar niet over het concept en de toepassing ervan. Laten we ons daar dus op richten.
Hoe zijn ze met elkaar verbonden?
Mathematisch gezien is SST = SSR + SSE.

De grondgedachte is als volgt: de totale variabiliteit van de gegevensverzameling is gelijk aan de variabiliteit die door de regressielijn wordt verklaard plus de onverklaarde variabiliteit, die als fout bekend staat.

Gezien een constante totale variabiliteit, zal een lagere fout een betere regressie opleveren. Omgekeerd zal een grotere fout een minder krachtige regressie tot gevolg hebben. En dat is wat u moet onthouden, ongeacht de notatie.
De volgende stap: De R-kwadraat
Wel, als u niet zeker weet waarom we al die sommen van kwadraten nodig hebben, hebben we precies het juiste hulpmiddel voor u. De R-kwadraat. Wilt u meer weten? Duik dan in de gelinkte tutorial waar je zult begrijpen hoe het de verklarende kracht van een lineaire regressie meet!
***
Interesseerd om meer te leren? U kunt uw vaardigheden van goed naar geweldig brengen met onze cursus statistiek.
Probeer gratis een cursus statistiek
Volgende tutorial: Het meten van variabiliteit met de R-kwadraat