Guinguette Marais Poitevin

Inhoud:

• Wat is een T-Test?
• De T Score
• T Waarden en P Waarden
• Bereken de T Test
• Wat is een Gekoppelde T Test (Paired Samples T Test)?

Wat is een T Test?

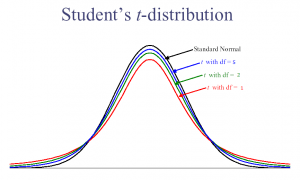
Verschillende vrijheidsgraden voor studenten-T.

De t-test vertelt je hoe significant de verschillen tussen groepen zijn; met andere woorden, hij laat je weten of die verschillen (gemeten in gemiddelden) door toeval zouden kunnen zijn ontstaan.

Een heel eenvoudig voorbeeld: Stel, u bent verkouden en u probeert een natuurgeneeskundig middel. Uw verkoudheid duurt een paar dagen. De volgende keer dat je verkouden bent, koop je een vrij verkrijgbaar geneesmiddel en de verkoudheid duurt een week. U ondervraagt uw vrienden en zij vertellen u allemaal dat hun verkoudheid korter duurde (gemiddeld 3 dagen) toen zij het homeopathische middel gebruikten. Wat u echt wilt weten is of deze resultaten herhaalbaar zijn. Een t-toets kan u dat vertellen door de gemiddelden van de twee groepen te vergelijken en u te laten weten hoe groot de kans is dat die resultaten toevallig zijn.

Een ander voorbeeld: Student’s T-tests kunnen in het echte leven worden gebruikt om gemiddelden te vergelijken. Een farmaceutisch bedrijf wil bijvoorbeeld een nieuw medicijn tegen kanker testen om te zien of het de levensverwachting verbetert. In een experiment is er altijd een controlegroep (een groep die een placebo, of “suikerpil” krijgt). De controlegroep kan een gemiddelde levensverwachting van +5 jaar hebben, terwijl de groep die het nieuwe geneesmiddel krijgt een levensverwachting van +6 jaar kan hebben. Het lijkt erop dat het medicijn zou kunnen werken. Maar het zou te wijten kunnen zijn aan een toevalstreffer. Om dit te testen, zouden onderzoekers een Student’s t-test gebruiken om uit te vinden of de resultaten herhaalbaar zijn voor een hele populatie.

Heb je nog steeds problemen? Chegg.com koppelt je aan een virtuele tutor (en de eerste 30 minuten zijn gratis!).

De T-Score.

De t-score is een verhouding tussen het verschil tussen twee groepen en het verschil binnen de groepen. Hoe groter de t-score, hoe meer verschil er is tussen de groepen. Hoe kleiner de t-score, hoe meer overeenkomst er is tussen de groepen. Een t-score van 3 betekent dat de groepen drie keer zo veel van elkaar verschillen als ze binnen elkaar verschillen. Wanneer je een t-test uitvoert, geldt: hoe groter de t-waarde, hoe waarschijnlijker het is dat de resultaten herhaalbaar zijn.

• Een grote t-score vertelt je dat de groepen verschillend zijn.
• Een kleine t-score vertelt je dat de groepen vergelijkbaar zijn.

T-waarden en P-waarden

Hoe groot is “groot genoeg”? Bij elke t-waarde hoort een p-waarde. Een p-waarde is de waarschijnlijkheid dat de resultaten van uw steekproef door toeval zijn verkregen. P-waarden gaan van 0% tot 100%. Ze worden meestal als decimaal geschreven. Bijvoorbeeld, een p-waarde van 5% is 0,05. Lage p-waarden zijn goed; ze geven aan dat uw gegevens niet toevallig zijn verkregen. Bijvoorbeeld, een p-waarde van .01 betekent dat er slechts 1% kans is dat de resultaten van een experiment toevallig zijn. In de meeste gevallen wordt een p-waarde van 0,05 (5%) geaccepteerd om aan te geven dat de gegevens geldig zijn.

Berekenen van de statistiek / Soorten tests

Er zijn drie hoofdtypen t-tests:

• Een Independent Samples t-test vergelijkt de gemiddelden van twee groepen.
• Een gepaarde t-toets vergelijkt de gemiddelden van dezelfde groep op verschillende tijdstippen (bijvoorbeeld een jaar na elkaar).
• Een t-toets met één steekproef vergelijkt het gemiddelde van één groep met een bekend gemiddelde.

Je wilt de toets waarschijnlijk niet met de hand berekenen (de wiskunde kan erg rommelig worden, maar als je erop staat, vind je de stappen voor een onafhankelijke t-toets hier.

Gebruik de volgende hulpmiddelen om de t-toets te berekenen:
Hoe doe je een T-toets in Excel.
T-toets in SPSS.
T-verdeling op de TI 89.
T-verdeling op de TI 83.

Wat is een gepaarde T-toets (Paired Samples T Test / Afhankelijke Steekproeven T-toets)?

Een gepaarde t-toets (ook wel een correlated pairs t-toets, een gepaarde steekproeven t-toets of afhankelijke steekproeven t-toets genoemd) is wanneer je een t-toets uitvoert op afhankelijke steekproeven. Afhankelijke steekproeven zijn in wezen met elkaar verbonden – het zijn tests op dezelfde persoon of hetzelfde ding. Bijvoorbeeld:

• Knee MRI-kosten in twee verschillende ziekenhuizen,
• Twee tests bij dezelfde persoon voor en na de training,
• Twee bloeddrukmetingen bij dezelfde persoon met verschillende apparatuur.

Wanneer kies je een gepaarde T-test / Paired Samples T Test / Dependent Samples T Test

Kies de gepaarde t-test als je twee metingen op hetzelfde item, persoon of ding hebt. U moet deze test ook kiezen als u twee items hebt die worden gemeten met een unieke voorwaarde. U meet bijvoorbeeld de veiligheidsprestaties van auto’s bij Vehicle Research and Testing en onderwerpt de auto’s aan een reeks crashtests. Hoewel de fabrikanten verschillend zijn, onderwerpt u ze aan dezelfde omstandigheden.

Bij een “gewone” twee-monsters t-toets vergelijkt u de gemiddelden van twee verschillende steekproeven. U kunt bijvoorbeeld twee verschillende groepen medewerkers van de klantenservice testen op een bedrijfsgerelateerde test of studenten van twee universiteiten testen op hun Engelse vaardigheden. Als je van elke groep afzonderlijk een willekeurige steekproef neemt en ze aan verschillende voorwaarden voldoen, zijn je steekproeven onafhankelijk en moet je een onafhankelijke steekproeven t-toets uitvoeren (ook wel tussen-steekproeven en ongepaarde-steekproeven genoemd).

De nulhypothese voor de onafhankelijke steekproeven t-toets is μ1 = μ2. Met andere woorden, er wordt aangenomen dat de gemiddelden gelijk zijn. Bij de gepaarde t-toets is de nulhypothese dat het paarsgewijze verschil tussen de twee toetsen gelijk is (H0: µd = 0). Het verschil tussen de twee toetsen is heel subtiel; welke je kiest, hangt af van je dataverzamelingsmethode.

Paired Samples T Test By hand

Voorbeeldvraag: Bereken een gepaarde t-toets met de hand voor de volgende gegevens: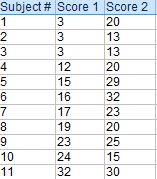

Stap 1: Trek elke Y-score af van elke X-score.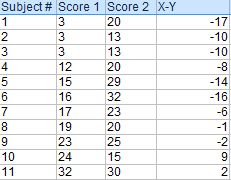

Stap 2: Tel alle waarden uit stap 1 bij elkaar op.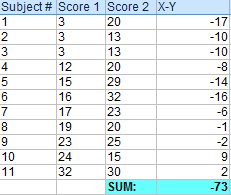

Stap 3: Kwadrateer de verschillen uit Stap 1.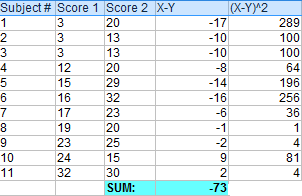

Stap 4: Tel alle gekwadrateerde verschillen uit Stap 3 bij elkaar op.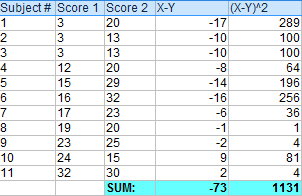

Stap 5: Gebruik de volgende formule om de t-score te berekenen: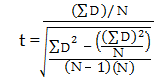

• ΣD: Som van de verschillen (som van X-Y uit stap 2)
• ΣD2: Som van de gekwadrateerde verschillen (uit stap 4)
• (ΣD)2: Som van de verschillen (uit stap 2), gekwadrateerd.

Als u niet bekend bent met Σ, wilt u misschien eerst meer lezen over sommatienotatie.

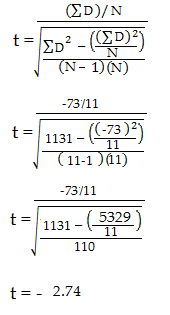
Step 6: Trek 1 af van de steekproefgrootte om de vrijheidsgraden te krijgen. We hebben 11 items, dus 11-1 = 10.

Stap 7: vind de p-waarde in de t-tabel, met behulp van de vrijheidsgraden in stap 6. Als u geen alfaniveau hebt opgegeven, gebruik dan 0,05 (5%). Voor dit voorbeeldprobleem, met df = 10, is de t-waarde 2,228.

Stap 8: Vergelijk uw t-tabelwaarde uit stap 7 (2,228) met uw berekende t-waarde (-2,74). De berekende t-waarde is groter dan de tabelwaarde bij een alfaniveau van .05. De p-waarde is kleiner dan het alfa-niveau: p <.05. We kunnen de nulhypothese verwerpen dat er geen verschil is tussen de gemiddelden.

Note: U kunt het minteken negeren bij het vergelijken van de twee t-waarden, want &pm; geeft de richting aan; de p-waarde blijft voor beide richtingen gelijk.

Kijk op ons YouTube-kanaal voor meer hulp en tips op het gebied van statistieken!

Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp. 50-55, 1956.

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!