Hoe ga je om met afhankelijke gebeurtenissen
Het leven zit vol willekeurige gebeurtenissen! Je moet er een “gevoel” voor krijgen om een slim en succesvol persoon te zijn.
Onafhankelijke gebeurtenissen
Gebeurtenissen kunnen “Onafhankelijk” zijn, wat betekent dat elke gebeurtenis niet wordt beïnvloed door andere gebeurtenissen.

Voorbeeld: Het opgooien van een munt.
Elke opgooi van een munt is een perfect op zichzelf staand iets.
Wat het in het verleden heeft gedaan, heeft geen invloed op de huidige opgooi.
De kans is gewoon 1 op 2, of 50%, net als bij ELKE opgooi van de munt.
Dus elke opgooi is een Onafhankelijke Gebeurtenis.
Afhankelijke Gebeurtenissen
Maar gebeurtenissen kunnen ook “afhankelijk” zijn … wat betekent dat ze kunnen worden beïnvloed door eerdere gebeurtenissen ….

Voorbeeld: Knikkers in een zak
2 blauwe en 3 rode knikkers zitten in een zak.
Wat is de kans dat je een blauwe knikker krijgt?
De kans is 2 op 5
Maar nadat je er een uit hebt gehaald verandert de kans!
Dus de volgende keer:
als we eerder een rode knikker hebben gekregen, dan is de kans op een blauwe knikker de volgende keer 2 op 4
als we eerder een blauwe knikker hebben gekregen, dan is de kans op een blauwe knikker 1 op 4
Dit komt omdat we knikkers uit de zak halen.
Dus de volgende gebeurtenis is afhankelijk van wat er in de vorige gebeurtenis is gebeurd, en wordt afhankelijk genoemd.
Vervanging
Opmerking: als we de knikkers in de zak elke keer vervangen, dan veranderen de kansen niet en zijn de gebeurtenissen onafhankelijk:
- Met Vervanging: de gebeurtenissen zijn Onafhankelijk (de kansen veranderen niet)
- Zonder Vervanging: de gebeurtenissen zijn Afhankelijk (de kansen veranderen)
Onafhankelijke gebeurtenissen is waar we hier naar kijken.
Boomdiagram
Een boomdiagram is een prachtige manier om ons voor te stellen wat er gaande is, dus laten we er een maken voor ons knikkervoorbeeld.
Er is een kans van 2/5 om een blauwe knikker te pakken, en een kans van 3/5 voor een rode:
We kunnen nog een stap verder gaan en kijken wat er gebeurt als we een tweede knikker pakken:
Als er eerst een blauwe knikker werd gekozen, is er nu een kans van 1/4 op een blauwe knikker en een kans van 3/4 op een rode knikker.
Als er eerst een rode knikker is gekozen, is er nu een kans van 2/4 op het krijgen van een blauwe knikker en een kans van 2/4 op het krijgen van een rode knikker.
Nu kunnen we vragen beantwoorden als “Wat is de kans dat je 2 blauwe knikkers trekt?”
Antwoord: het is een kans van 2/5 gevolgd door een kans van 1/4:
Heb je gezien hoe we de kansen hebben vermenigvuldigd? En als resultaat 1/10 kregen.
De kans om 2 blauwe knikkers te trekken is 1/10
Notatie
Wij zijn dol op notatie in de wiskunde! Het betekent dat we dan de kracht van algebra kunnen gebruiken om met de ideeën te spelen. Dus hier is de notatie voor waarschijnlijkheid:
P(A) betekent “Waarschijnlijkheid van gebeurtenis A”
In ons knikkervoorbeeld Gebeurtenis A is “als eerste een blauwe knikker krijgen” met een waarschijnlijkheid van 2/5:
P(A) = 2/5
En gebeurtenis B is “als tweede een blauwe knikker krijgen” … maar daarvoor hebben we 2 keuzes:
- Als we eerst een Blauwe Knikker hebben gekregen is de kans nu 1/4
- Als we eerst een Rode Knikker hebben gekregen is de kans nu 2/4
Dus moeten we zeggen welke we willen, en het symbool “|” gebruiken om “gegeven” te betekenen:
P(B|A) betekent “gebeurtenis B gegeven gebeurtenis A”
Met andere woorden, gebeurtenis A is al gebeurd, wat is nu de kans op gebeurtenis B?
P(B|A) wordt ook wel de “Voorwaardelijke Waarschijnlijkheid” van B gegeven A genoemd.
En in ons geval:
P(B|A) = 1/4
Dus de kans dat je 2 blauwe knikkers krijgt is:
En we schrijven het als
“Waarschijnlijkheid van gebeurtenis A en gebeurtenis B is gelijk aan
de waarschijnlijkheid van gebeurtenis A maal de waarschijnlijkheid van gebeurtenis B gegeven gebeurtenis A”
Laten we het volgende voorbeeld eens doen met alleen notatie:
Voorbeeld: Het trekken van 2 Koningen uit een kaartspel
Voorval A is het trekken van een Koning als eerste, en gebeurtenis B is het trekken van een Koning als tweede.
Voor de eerste kaart is de kans om een Koning te trekken 4 op 52 (er zijn 4 Koningen in een kaartspel van 52 kaarten):
P(A) = 4/52
Maar na het verwijderen van een Koning uit het kaartspel is de kans dat de tweede getrokken kaart een Koning is kleiner (slechts 3 van de 51 overgebleven kaarten zijn Koningen):
P(B|A) = 3/51
En dus:
P(A en B) = P(A) x P(B|A) =(4/52)x (3/51) = 12/2652 = 1/221
Dus de kans om 2 Koningen te krijgen is 1 op 221, of ongeveer 0.5%
Het vinden van verborgen gegevens
Met behulp van Algebra kunnen we ook het onderwerp van de formule “veranderen”, zoals dit:
| Start met: | P(A en B) = P(A) x P(B|A) | |
| Verwissel de kanten: | P(A) x P(B|A) = P(A en B) | |
| P(B|A) = P(A en B) / P(A) |
En we hebben weer een handige formule:
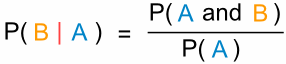
“De waarschijnlijkheid van gebeurtenis B gegeven gebeurtenis A is gelijk aan
de waarschijnlijkheid van gebeurtenis A en gebeurtenis B gedeeld door de waarschijnlijkheid van gebeurtenis A
Voorbeeld: IJs
70% van je vrienden houdt van Chocolade, en 35% houdt van Chocolade EN van Aardbei.
Welk percentage van degenen die Chocolade lekker vinden, vinden ook Aardbei lekker?
P(Aardbei|Chocolade) = P(Chocolade en Aardbei) / P(Chocolade)
50% van je vrienden die van Chocolade houden, houden ook van Aardbei

Groot Voorbeeld: Voetbalwedstrijd
Je gaat voetballen, en wilt de keeper zijn, maar dat hangt ervan af wie vandaag de coach is:
- met coach Sam is de kans dat je keeper bent 0,5
- met coach Alex is de kans dat je keeper bent 0.3
Sam is vaker Coach … ongeveer 6 van de 10 wedstrijden (een waarschijnlijkheid van 0.6).
Dus, wat is de waarschijnlijkheid dat je vandaag Doelman bent?
Laten we een boomdiagram bouwen. Eerst laten we de twee mogelijke coaches zien: Sam of Alex:
De kans dat je Sam krijgt is 0,6, dus de kans dat je Alex krijgt moet 0,4 zijn (samen is de kans 1)
Nu, als je Sam krijgt, is er 0,5 kans dat je Goalie bent (en 0,5 dat je geen Goalie bent):
Nu, als je Sam krijgt, is er 0,5 kans dat je Goalie bent (en 0.5 van het niet zijn van Goalie):
Als je Alex krijgt, is er 0,3 kans dat je Goalie bent (en 0.7 niet):
Het boomdiagram is compleet, laten we nu de totale waarschijnlijkheid berekenen. Onthoud dat:
P(A en B) = P(A) x P(B|A)
Hier volgt hoe je dat doet voor de “Sam, Ja”-tak:
(Als we de 0.6 kans dat Sam coach is maal de 0,5 kans dat Sam jou keeper laat zijn, komen we uit op een kans van 0,3.)
Maar we zijn nog niet klaar! We hebben Alex als Coach niet meegenomen:
Een kans van 0,4 op Alex als Coach, gevolgd door een kans van 0,3 geeft 0,12
En de twee “Ja”-takken van de boom samen maken:
0,3 + 0,12 = 0.42 kans om vandaag keeper te zijn
(Dat is een kans van 42%)
Check
Een laatste stap: voltooi de berekeningen en controleer of ze optellen tot 1:
0.3 + 0,3 + 0,12 + 0,28 = 1
Ja, ze tellen op tot 1, dus dat ziet er goed uit.
Vrienden en willekeurige getallen
Hier volgt een heel ander voorbeeld van Voorwaardelijke Waarschijnlijkheid.
4 vrienden (Alex, Blake, Chris en Dusty) kiezen elk een willekeurig getal tussen 1 en 5. Wat is de kans dat een van hen hetzelfde getal kiest?
Laten we onze vrienden een voor een optellen …
Eerst, wat is de kans dat Alex en Blake hetzelfde getal hebben?
Blake vergelijkt zijn getal met dat van Alex. Er is een kans van 1 op 5 dat ze overeenkomen.
Als boomdiagram:
Note: “Ja” en “Nee” samen maakt 1
(1/5 + 4/5 = 5/5 = 1)
Nu, laten we Chris erbij betrekken …
Maar er zijn nu twee gevallen te overwegen:
- Als Alex en Blake overeenkwamen, dan heeft Chris maar één getal om mee te vergelijken.
- Maar als Alex en Blake niet overeenkwamen, dan heeft Chris twee getallen om mee te vergelijken.
En dan krijgen we dit:
Voor de bovenste regel (Alex en Blake matchen wel) hebben we al een match (een kans van 1/5).
Maar voor de “Alex en Blake kwamen niet overeen” is er nu een kans van 2/5 dat Chris overeenkomt (omdat Chris zijn nummer mag vergelijken met zowel Alex als Blake).
En we kunnen de gecombineerde kans berekenen door de kansen te vermenigvuldigen die nodig waren om er te komen:
Volgend het “Nee, Ja” pad … is er een 4/5 kans op Nee, gevolgd door een 2/5 kans op Ja:
Volgend het “Nee, Nee” pad …. is er een kans van 4/5 op Nee, gevolgd door een kans van 3/5 op Nee:
Ook valt op dat als we alle kansen bij elkaar optellen we nog steeds 1 krijgen (een goede controle dat we ons niet hebben vergist):
(5/25) + (8/25) + (12/25) = 25/25 = 1
Nu wat gebeurt er als we Dusty meerekenen?
Het is hetzelfde idee, alleen meer ervan:
OK, dat zijn alle 4 vrienden, en de “Ja”-kansen samen maken 101/125:
Antwoord: 101/125
Maar hier is iets interessants … als we het “Nee”-pad volgen, kunnen we alle andere berekeningen overslaan en ons leven eenvoudiger maken:
De kansen om niet te matchen zijn:
(4/5) × (3/5) × (2/5) = 24/125
Dus de kans op matching is:
1 – (24/125) = 101/125
(En daar hadden we niet echt een boomdiagram voor nodig!)
















