Guinguette Marais Poitevin

Comment gérer les événements dépendants

La vie est pleine d’événements aléatoires ! Vous devez les  » sentir  » pour être une personne intelligente et performante.

Événements indépendants

Les événements peuvent être  » indépendants « , ce qui signifie que chaque événement n’est affecté par aucun autre événement.

Événements dépendants

Mais les événements peuvent aussi être  » dépendants « … ce qui signifie qu’ils peuvent être affectés par des événements précédents….

C’est parce que nous retirons des billes du sac.

Donc l’événement suivant dépend de ce qui s’est passé lors de l’événement précédent, et est appelé dépendant.

Les événements dépendants sont ce que nous regardons ici.

Diagramme en arbre

Un diagramme en arbre:estunmagnifiquemoyend’imaginercequisepasse,alorsconstruisons-en un pour notre exemple de billes.

Il y a 2/5 de chances de tirer une bille Bleue, et 3/5 de chances pour la Rouge:

Nous pouvons aller plus loin et voir ce qui se passe lorsque nous tirons une deuxième bille :

Si une bille bleue a été sélectionnée en premier, il y a maintenant 1/4 de chance d’obtenir une bille bleue et 3/4 de chance d’obtenir une bille rouge.

Si une bille rouge a été sélectionnée en premier, il y a maintenant une chance sur quatre d’obtenir une bille bleue et une chance sur quatre d’obtenir une bille rouge.

Notation

Nous adorons la notation en mathématiques ! Cela signifie que nous pouvons ensuite utiliser la puissance de l’algèbre pour jouer avec les idées. Voici donc la notation des probabilités :

P(A) signifie  » Probabilité de l’événement A « 

Dans notre exemple des billes, l’événement A est  » obtenir une bille bleue en premier  » avec une probabilité de 2/5 :

P(A) = 2/5

Et l’événement B est  » obtenir une bille bleue en second  » …. mais pour cela nous avons 2 choix :

• Si nous avons obtenu une bille bleue en premier, la chance est maintenant de 1/4
• Si nous avons obtenu une bille rouge en premier, la chance est maintenant de 2/4

Donc nous devons dire lequel nous voulons, et utiliser le symbole « | » pour signifier « donné » :

P(B|A) signifie « Événement B donné événement A »

En d’autres termes, l’événement A s’est déjà produit, maintenant quelle est la chance de l’événement B ?

P(B|A) est également appelée la  » probabilité conditionnelle  » de B étant donné A.

Et dans notre cas :

P(B|A) = 1/4

Donc la probabilité d’obtenir 2 billes bleues est de :

Et nous l’écrivons sous la forme

.

« La probabilité d’un événement A et d’un événement B est égale
à la probabilité de l’événement A multipliée par la probabilité de l’événement B étant donné l’événement A »

Faisons l’exemple suivant en utilisant uniquement la notation :

Découvrir des données cachées

En utilisant l’algèbre, nous pouvons également « changer le sujet » de la formule, comme ceci:

Débutant par :		P(A et B) = P(A) x P(B|A)
Intervertir les côtés :		P(A) x P(B|A) = P(A et B)
Diviser par P(A) :		P(B|A) = P(A et B) / P(A)

Et nous avons une autre formule utile :

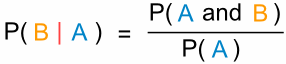
« La probabilité de l’événement B étant donné l’événement A est égale
à la probabilité de l’événement A et de l’événement B divisée par la probabilité de l’événement A

Grand exemple : Match de foot

Vous partez au foot, et vous voulez être le Gardien de but, mais cela dépend de qui est l’Entraîneur aujourd’hui :

• avec l’Entraîneur Sam la probabilité d’être Gardien de but est de 0,5
• avec l’Entraîneur Alex la probabilité d’être Gardien de but est de 0.3

Sam est Coach plus souvent… environ 6 matchs sur 10 (une probabilité de 0,6).

Donc, quelle est la probabilité que vous soyez Gardien de but aujourd’hui ?

Construisons un diagramme en arbre. Tout d’abord, nous montrons les deux entraîneurs possibles : Sam ou Alex:

La probabilité d’obtenir Sam est de 0,6, donc la probabilité d’Alex doit être de 0,4 (ensemble la probabilité est de 1)

Maintenant, si vous obtenez Sam, il y a 0,5 probabilité d’être Gardien de but (et 0.5 de ne pas être Goalie):

Si vous obtenez Alex, il y a 0,3 probabilité d’être Goalie (et 0.7 pas):

Le diagramme en arbre est complet, calculons maintenant les probabilités globales. Rappelez-vous que :

P(A et B) = P(A) x P(B|A)

Voici comment procéder pour la branche  » Sam, oui  » :

(Lorsque nous prenons les 0.6 chance que Sam soit entraîneur fois la 0,5 chance que Sam te laisse être Gardien de but, nous obtenons une chance de 0,3.)

Mais nous n’avons pas encore fini ! Nous n’avons pas inclus Alex comme entraîneur :

Une chance de 0,4 qu’Alex soit entraîneur, suivie d’une chance de 0,3 donne 0,12

Et les deux branches  » Oui  » de l’arbre ensemble font :

0,3 + 0,12 = 0.42 probabilité d’être gardien de but aujourd’hui

(Soit une chance de 42%)

Vérifier

Une dernière étape : compléter les calculs et s’assurer que leur somme est égale à 1:

0.3 + 0,3 + 0,12 + 0,28 = 1

Oui, leur somme est égale à 1, cela semble donc correct.

Des amis et des nombres aléatoires

Voici un autre exemple assez différent de probabilité conditionnelle.

4 amis (Alex, Blake, Chris et Dusty) choisissent chacun un nombre aléatoire entre 1 et 5. Quelle est la chance que l’un d’entre eux ait choisi le même numéro ?

Ajoutons nos amis un par un…

D’abord, quelle est la chance qu’Alex et Blake aient le même numéro ?

Blake compare son numéro à celui d’Alex. Il y a une chance sur 5 qu’il y ait correspondance.

Sous forme d’arborescence :

Note :  » Oui  » et  » Non  » réunis font 1
(1/5 + 4/5 = 5/5 = 1)

Maintenant, incluons Chris ….

Mais il y a maintenant deux cas à considérer :

• Si Alex et Blake ont bien correspondu, alors Chris n’a qu’un seul nombre à comparer.
• Mais si Alex et Blake n’ont pas correspondu, alors Chris a deux nombres à comparer.

Et nous obtenons ceci :

Pour la ligne supérieure (Alex et Blake ont concordé), nous avons déjà une concordance (une chance de 1/5).

Mais pour le  » Alex et Blake n’ont pas correspondu « , il y a maintenant une chance sur 2/5 que Chris corresponde (parce que Chris a la possibilité de faire correspondre son numéro à la fois à Alex et à Blake).

Et nous pouvons calculer la chance combinée en multipliant les chances qu’il a fallu pour y arriver :

Notez également que lorsque nous additionnons toutes les chances, nous obtenons toujours 1 (une bonne vérification que nous n’avons pas fait d’erreur) :

(5/25) + (8/25) + (12/25) = 25/25 = 1

Que se passe-t-il maintenant lorsque nous incluons Dusty ?

C’est la même idée, mais en plus grand nombre:

OK, cela fait les 4 amis, et les chances de « Oui » ensemble font 101/125:

Réponse : 101/125