Qu’est-ce que la probabilité conjointe ?
La probabilité conjointe est un type de mesure trouvée en calculant la probabilité que deux événements se produisent ensemble. En d’autres termes, c’est la probabilité que l’événement X se produise en même temps que l’événement Y, comme une intersection de deux événements.
Probabilité conjointe pour les événements dépendants
Pour mesurer la probabilité conjointe, les deux événements doivent se produire en même temps et doivent être indépendants l’un de l’autre. Cela signifie que la probabilité conjointe pour les événements dépendants ne peut pas être déterminée.
Disons que vous voulez déterminer s’il va pleuvoir au moment où il y a des nuages dans le ciel. Ces deux événements sont dépendants l’un de l’autre car lorsqu’il pleut, il y aura très probablement une présence de nuages. Par conséquent, ces événements sont dépendants les uns des autres.
Au lieu de la probabilité conjointe, il faut utiliser la probabilité conditionnelle pour les événements dépendants.
Probabilité conjointe pour les événements indépendants
Comme mentionné, pour déterminer la probabilité conjointe, les deux événements doivent être indépendants l’un de l’autre. Par exemple, la probabilité d’obtenir « pile » ou « face » à un tirage au sort sont des événements indépendants. En d’autres termes, la probabilité d’obtenir une queue lors du premier lancer n’aura pas d’impact sur la probabilité d’obtenir une tête lorsque vous lancez la pièce une deuxième fois.
Comment calculer la probabilité conjointe
Lorsque vous apprenez à calculer la probabilité conjointe, il est crucial de comprendre que la formule exige que les deux événements soient indépendants l’un de l’autre. Cela signifie que le résultat d’un événement ne peut pas affecter l’impact du résultat de l’autre événement. Avant de calculer la probabilité conjointe, demandez-vous si le résultat d’un événement va influencer le résultat de l’autre.
Puisque la probabilité conjointe peut être décrite comme » l’intersection de deux événements « , la formule inclura les deux – et comment ils peuvent se croiser.
Dans la formule ci-dessous, vous verrez le symbole « ∩ » utilisé pour représenter une intersection. Pour les apprenants plus visuels, l’utilisation d’un diagramme de Venn est la meilleure façon d’illustrer comment deux événements peuvent se croiser ensemble.
Formule de probabilité conjointe
La formule de probabilité conjointe est la suivante :
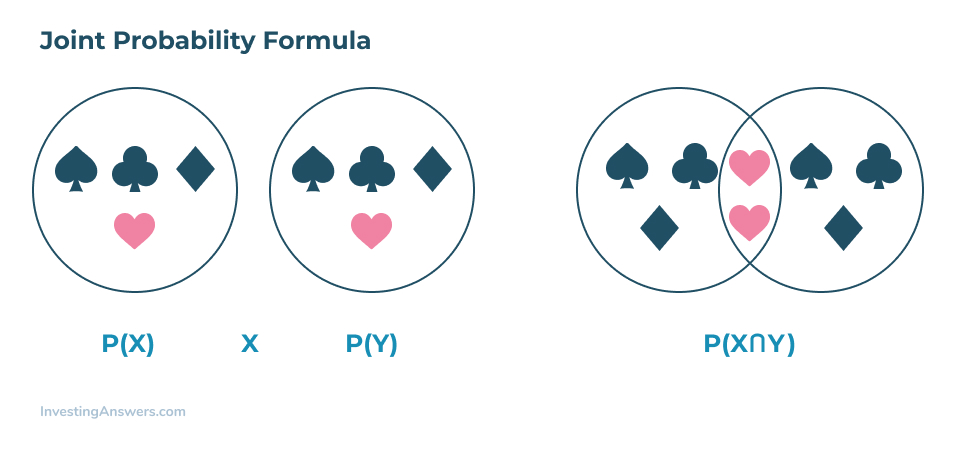
Dans cette formule, X et Y représentent tous deux deux des événements différents qui se croisent, et P est égale à la probabilité de jonction de X et de Y.
Les autres façons d’exprimer la formule de probabilité conjointe sont également P( X et Y) et P(XY).
Exemple de probabilité conjointe #1
Disons que vous voulez calculer la probabilité conjointe pour un lancer de pièce de monnaie où vous pouvez obtenir une queue (événement X) suivie d’une tête (événement Y).
Dans ce cas, la probabilité de l’événement X est de 50 % (ou 0,5) et la probabilité de l’événement Y est également de 50 %. Maintenant, nous pouvons brancher les chiffres dans la formule :
P(0,5 x 0,5) = 0,25 ou 25%
Ce qui signifie que la probabilité conjointe d’obtenir une queue puis une tête lors d’un tirage au sort est de 25%.
Probabilité conjointe Exemple #2
Vous lancez un dé et vous voulez calculer la probabilité conjointe de faire apparaître le chiffre six deux fois de suite. La probabilité de suivre un six la première fois est de 1/6, car il n’y a que six options dans un dé à six faces. Cela équivaut à ⅙, ou 17% (en décimales, cela fait 0,1666). C’est la même chose pour lancer un six la deuxième fois.
En utilisant ces informations, nous pouvons déterminer que la probabilité conjointe de lancer un six la première et la deuxième fois sera la suivante :
P(0,1666 x 0,1666) = 0,02777 ou 2,8 %
Cela signifie que vous avez une probabilité de 2,8 % que les deux événements se produisent.
Quand utiliser la probabilité conjointe
La probabilité conjointe est utile lorsque vous voulez mesurer deux événements indépendants pour déterminer s’ils peuvent se produire simultanément.
Comment la probabilité conjointe est-elle utilisée par rapport à l’investissement ?
La probabilité conjointe est une statistique utile pour les analystes et les statisticiens lorsque deux phénomènes observables ou plus peuvent se produire simultanément. Par exemple, lorsqu’une baisse de la moyenne industrielle Dow Jones s’accompagne d’une perte substantielle de la valeur du dollar.
Vous pouvez également comparer deux actions distinctes pour voir si la valeur de l’une augmente (et si l’autre le fera aussi).