Objectivos de Aprendizagem
Ao fim desta secção, será capaz de:
- Explicar como os intervalos de tempo podem ser medidos diferentemente em diferentes quadros de referência.
- Descrever como distinguir um intervalo de tempo adequado de um intervalo de tempo dilatado.
- Descrever o significado da experiência muon.
- Explicar porque é que o paradoxo gémeo não é uma contradição.
- Calcular a dilatação temporal dada a velocidade de um objecto num dado quadro.
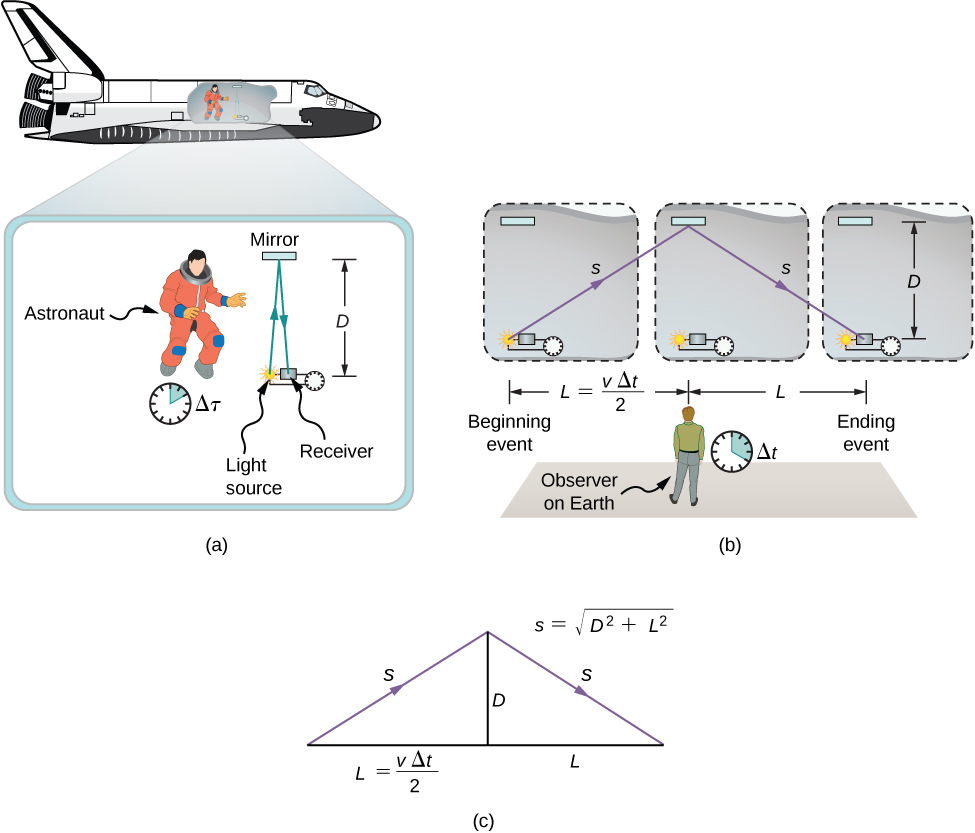
A análise da simultaneidade mostra que os postulados de Einstein implicam um efeito importante: Os intervalos de tempo têm valores diferentes quando medidos em diferentes quadros de inércia. Suponha, por exemplo, que um astronauta mede o tempo que leva para um impulso de luz percorrer uma distância perpendicular à direcção do movimento do seu navio (em relação a um observador terrestre), ricochetear num espelho, e regressar (Figura \PageIndex{1a})). Como se compara o tempo decorrido que o astronauta mede na nave com o tempo decorrido que um observador terrestre mede observando o que está a acontecer na nave?
p>Examinar esta questão leva a um resultado profundo. O tempo decorrido para um processo depende do observador que o está a medir. Neste caso, o tempo medido pelo astronauta (dentro da nave espacial onde o astronauta está em repouso) é menor do que o tempo medido pelo observador ligado à terra (para quem o astronauta se desloca). O tempo decorrido para o mesmo processo é diferente para os observadores, porque a distância que o pulso de luz percorre na armação do astronauta é menor do que na armação ligada à terra, como se vê na Figura 1b). A luz viaja à mesma velocidade em cada moldura, pelo que demora mais tempo a percorrer a maior distância na moldura ligada à terra.
Definition: Time Dilation
Time dilation is the lengthening of the time interval between two events for an observer in an inertial frame that is moving with respect to the rest frame of the events (in which the events occur at the same location).
Para comparar quantitativamente as medições de tempo nos dois quadros de inércia, podemos relacionar as distâncias na Figura 1b, depois expressar cada distância em termos do tempo de viagem (respectivamente, ou delta t) ou delta t) do pulso no quadro de referência correspondente. A equação resultante pode então ser resolvida para Delta t) em termos de Delta t).
Os comprimentos D e L na figura 1c) são os lados de um triângulo direito com hipotenusa. Do teorema de Pitágoras,
p>p> Os comprimentos de Pietágoras (2s) e (2L) são, respectivamente, as distâncias que o pulso de luz e a nave espacial percorrem no tempo na moldura do observador ligado à terra. O comprimento é a distância que o pulso de luz percorre no tempo na moldura do astronauta. Isto dá-nos três equações:
\ 2L &= v\Delta t; \ 2D &= c\Delta \tau. \{alinhamento*}]
Nota que utilizámos o segundo postulado de Einstein, tomando a velocidade da luz para ser c em ambos os quadros inercial. Substituímos estes resultados na expressão anterior do teorema de Pitágoras:
p> esquerda(c\dfrac{\Delta t}{2}{2}direita)^2 &= ^esquerda(c\dfrac{\Delta ^2 direita)^2 +esquerda(v\dfrac{\Delta t}{2}{2}direita)^2 ^2end{alinhamento*}]
Então reordenamos para obter
p>>p>Finalmente, resolvendo para o Delta, em termos de Delta, dá-nos factor relativista (muitas vezes chamado factor Lorentz) dado por
/p>p>e \(v) e \(c) são as velocidades do observador em movimento e da luz, respectivamente.
Nota a assimetria entre as duas medidas. Apenas uma delas é uma medição do intervalo de tempo entre dois eventos – emissão e chegada do pulso de luz – na mesma posição. É uma medição do intervalo de tempo no quadro de descanso de um único relógio. A medição no quadro de terra implica a comparação do intervalo de tempo entre dois eventos que ocorrem em locais diferentes. O intervalo de tempo entre eventos que ocorrem num único local tem um nome separado para o distinguir do tempo medido pelo observador ligado à terra, e usamos o símbolo separado \(\Delta \tau) para nos referirmos a ele ao longo deste capítulo.
Definição: O intervalo de tempo adequado entre dois eventos é o intervalo de tempo medido por um observador para quem ambos os eventos ocorrem no mesmo local.
A equação relacionada com o intervalo de tempo adequado entre dois eventos é verdadeiramente notável. Em primeiro lugar, como foi dito anteriormente, o tempo decorrido não é o mesmo para observadores diferentes que se deslocam um em relação ao outro, mesmo que ambos se encontrem em estruturas inercialmente. Um intervalo de tempo adequado para um observador que, tal como o astronauta, se move com o aparelho, é menor do que o intervalo de tempo para outros observadores. É o menor tempo medido possível entre dois eventos. O observador ligado à Terra vê os intervalos de tempo dentro do sistema em movimento como dilatados (ou seja, alongados) relativamente à forma como o observador em movimento em relação à Terra os vê dentro do sistema em movimento. Em alternativa, de acordo com o observador ligado à Terra, passa menos tempo entre os eventos dentro do quadro em movimento. Note-se que o tempo decorrido mais curto entre eventos está no quadro inercial em que o observador vê os eventos (por exemplo, a emissão e chegada do sinal luminoso) ocorrer no mesmo ponto.
Este efeito de tempo é real e não é causado por relógios imprecisos ou medições inadequadas. As medições do intervalo de tempo do mesmo evento diferem para os observadores em movimento relativo. A dilatação do tempo é uma propriedade intrínseca do próprio tempo. Todos os relógios em movimento relativo a um observador, incluindo os relógios biológicos, tais como o bater do coração de uma pessoa, ou o envelhecimento, são observados a correr mais lentamente em comparação com um relógio que está parado em relação ao observador.
Nota que se a velocidade relativa for muito inferior à velocidade da luz (v << c), então \(v^2/c^2\) é extremamente pequena, e os tempos decorridos são quase iguais. A baixas velocidades, a física baseada na relatividade moderna aborda a física clássica – todas as experiências quotidianas envolvem efeitos relativistas muito pequenos. No entanto, para velocidades próximas da velocidade da luz, (v^2/c^2) está próximo de uma, pelo que oqrt{1 – v^2/c^2}) é muito pequeno e torna-se significativamente maior do que o delta t).
Half-Life of a Muon
Existem provas experimentais consideráveis de que a equação {Delta t = {gamma {Delta t} está correcta. Um exemplo é encontrado em partículas de raios cósmicos que chovem continuamente na Terra a partir do espaço profundo. Algumas colisões destas partículas com núcleos na atmosfera superior resultam em partículas de curta duração chamadas muões. A meia-vida (quantidade de tempo para metade de um material se decompor) de um muão é 1,52 μs quando está em repouso em relação ao observador que mede a meia-vida. Este é o intervalo de tempo adequado. Este curto tempo permite que muito poucos muões cheguem à superfície da Terra e sejam detectados se as suposições Newtonianas sobre o tempo e o espaço estiverem correctas. No entanto, os muões produzidos por partículas de raios cósmicos têm uma gama de velocidades, com alguns a moverem-se perto da velocidade da luz. Verificou-se que a meia-vida do muão, medida por um observador ligado à Terra (Delta t), varia com a velocidade exactamente como previsto pela equação (Delta t = Delta t = Delta t = Delta t). Quanto mais rápido o muon se move, mais tempo vive. Nós na Terra vemos o muon durar muito mais tempo do que a sua meia-vida prevê dentro da sua própria estrutura de repouso. Como visto da nossa moldura, o muon decai mais lentamente do que quando em repouso em relação a nós. Uma fracção muito maior de muões atinge o solo como resultado.
Antes de apresentarmos o primeiro exemplo de resolução de um problema em relatividade, indicamos uma estratégia que pode usar como orientação para estes cálculos.
ESTRATÉGIA DE RESOLUÇÃO DE PROBLEMAS: RELATIVIDADE
- Faça uma lista do que é dado ou que pode ser inferido a partir do problema, tal como indicado (identifique os conhecimentos). Procurar em particular informações sobre velocidade relativa v.
- Identificar exactamente o que precisa de ser determinado no problema (identificar as incógnitas).
Li>Tenham a certeza de compreender os aspectos conceptuais do problema antes de fazer quaisquer cálculos (expressar a resposta como uma equação). Decidir, por exemplo, qual o observador que vê o tempo dilatado ou a duração contraída antes de trabalhar com as equações ou utilizá-las para efectuar o cálculo. Se tiver pensado sobre quem vê o quê, quem se move com o evento a ser observado, quem vê o tempo adequado, etc., achará muito mais fácil determinar se o seu cálculo é razoável.li>Determinar o tipo primário de cálculo a ser feito para encontrar as incógnitas identificadas acima (fazer o cálculo). O resumo da secção será útil para determinar se está envolvida uma contracção de comprimento, energia cinética relativista, ou algum outro conceito.
Nota que não deve terminar durante o cálculo. Tal como referido no texto, deve frequentemente efectuar os seus cálculos a muitos dígitos para ver o efeito desejado. Pode arredondar no final da solução do problema, mas não utilize um número arredondado num cálculo subsequente. Verifique também a resposta para ver se ela é razoável: Será que faz sentido? Isto pode ser mais difícil para a relatividade, que tem poucos exemplos diários para proporcionar experiência com o que é razoável. Mas pode procurar velocidades superiores a c ou efeitos relativistas que estejam na direcção errada (tal como uma contracção temporal onde se esperava uma dilatação).
Exemplo \\i(PageIndex{1A}}): Dilatação temporal num veículo de alta velocidade
O veículo de tecnologia hipersónica 2 (HTV-2) é um veículo experimental de foguete capaz de viajar a 21.000 km/h (5830 m/s). Se um relógio electrónico no HTV-2 mede um intervalo de tempo de exactamente 1-s de duração, o que é que os observadores na Terra mediriam o intervalo de tempo a ser?
Estratégia
Aplicar a fórmula de dilatação temporal para relacionar o intervalo de tempo adequado do sinal no HTV-2 com o intervalo de tempo medido no solo.
Solução
- Identificar os conhecimentos: \(v = 5830m/s.\)
- Faz o cálculo. Use a expressão para {gamma} para determinar a partir de Delta t
\i>&
li>Identificar o desconhecido: \(delta t).li>Expressa a resposta como uma equação:
\
= 1.000000000189, s &= 1 {-10}s, s + 1.89 ^{-10}s. \{alinhamento*}]
Significação
A velocidade muito elevada do HTV-2 é ainda apenas 10-5 vezes a velocidade da luz. Os efeitos relativistas do HTV-2 são negligenciáveis para quase todos os fins, mas não são zero.
Que velocidades são relativistas?
Quão rápido deve um veículo viajar durante 1 segundo de tempo medido no relógio de um passageiro no veículo para diferir em 1% para um observador que o mede do solo no exterior?
Estratégia
Utilizar a fórmula de dilatação temporal para encontrar v/c para a relação de tempos dada.
p>Solução
- Identificar o conhecido:
\\
- Expressar a resposta como uma equação:
p>>&
li>Identificar o desconhecido: v/c.
= ^dfrac{1}{sqrt{1 – v^2/c^2}}delta ^tau ^dfrac{Delta ^delta t} &= \sqrt{1 – v^2/c^2} \\ esquerda(ddelta t) direita)2 &= 1 – ^dfrac{v^2}{c^2}{c^2} \\ dfrac{v}{c} &= \sqrt{1 – (\Delta \tau/\Delta t)^2}. \^end{align*}]
\
Significação
O resultado mostra que um objecto deve viajar a cerca de 10% da velocidade da luz para que o seu movimento produza efeitos relativistas de dilatação temporal significativos.
Cálculo de um Evento Relativista
p>Se um raio cósmico colidir com um núcleo na atmosfera superior da Terra produz um muão que tem uma velocidade \(v = 0,950c\). O muão viaja então a uma velocidade constante e vive 2,20 μs tal como medido no quadro de referência do muão. (Pode imaginar isto como o relógio interno do muon.) Quanto tempo vive o muon medido por um observador terrestre (Figura \PageIndex{2}}?
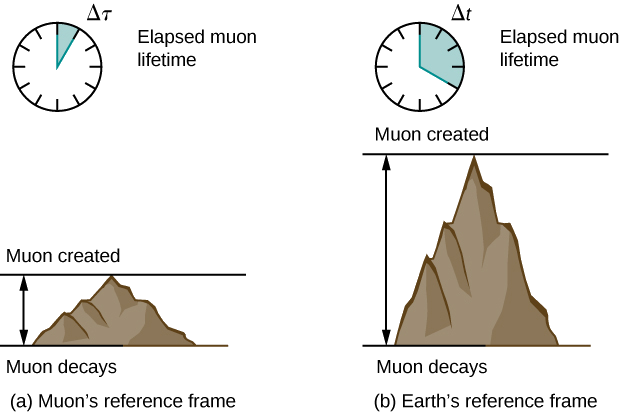
Como discutiremos mais tarde, no quadro de referência do muão, ele percorre uma distância menor do que a medida no quadro de referência da Terra.
Estratégia
Um relógio em movimento com o muon mede o tempo adequado do seu processo de decaimento, pelo que o tempo que nos é dado é {Delta \tau = 2,20mu s}). O observador ligado à terra mede como dado pela equação Delta t = Delta gamma). Como a velocidade é dada, podemos calcular o tempo no quadro de referência da Terra.
Solução
- Identificar os conhecimentos: \(v = 0,950c); {delta {tau = 2,20mu s}.
- Faz o cálculo. Usar a expressão para {gamma} para determinar a partir de {delta t}:
&=dfrac{1}{sqrt{1 – {v^2}{c^2}}delta {delta ^tau {&=dfrac{2.20mu s}{sqrt{1 – (0.950)^2}}} \\&= 7.05, \u s.|end{align*}]
Lembre-se de manter números extra significativos até à resposta final.
Identificar o desconhecido: \(delta t).li>Expressar a resposta como uma equação. Usar:
\\
com
\
Significado
Uma implicação deste exemplo é que porque \(\gamma = 3,20\) a 95,0% da velocidade da luz (\ v = 0,950c)), os efeitos relativistas são significativos. Os dois intervalos de tempo diferem por um factor de 3,20, quando classicamente seriam os mesmos. Diz-se que algo que se move a 0,950c é altamente relativista.
Exemplo \(\PageIndex{1B}}): Televisão relativista
Um ecrã não plano, de estilo mais antigo (Figura \PageIndex{3}}) funciona acelerando os electrões numa curta distância até à velocidade relativista, e depois utilizando campos electromagnéticos para controlar onde o feixe de electrões atinge uma camada fluorescente na parte da frente do tubo. Suponha que os electrões viajam a \(6,00 \postos 10^7 m/s) através de uma distância de 0,200m0,200m desde o início do feixe até ao ecrã.
- Qual é o tempo de viagem de um electrão no quadro de descanso do televisor?
- Qual é o tempo de viagem de um electrão no seu próprio quadro de descanso?
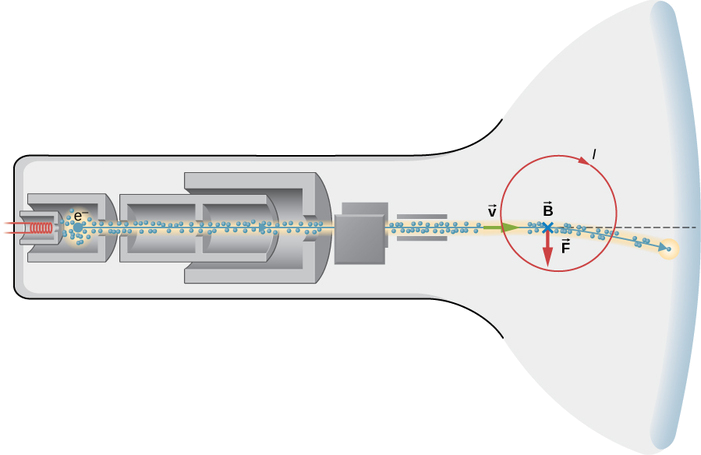
Estratégia para (a)
(a) Calcular o tempo a partir de \(vt = d\). Ainda que a velocidade seja relativista, o cálculo está inteiramente num quadro de referência, e a relatividade não está portanto envolvida.
Solução
- Identificar os conhecimentos:
/p>
- Expressar a resposta como uma equação:
\
- Faz o cálculo:
\i>&
li>Identificar o desconhecido: o tempo de viagem \\(Delta t\).
= 3,33 vezes 10^{-9} \s. {alinhamento*}]/li>/ol>
Significação
O tempo de viagem é extremamente curto, como se esperava. Como o cálculo está inteiramente dentro de um único quadro de referência, a relatividade não está envolvida, embora a velocidade do electrão esteja próxima de c.
Estratégia para (b)
(b) No quadro de referência do electrão, o tubo de vácuo está em movimento e o electrão está estacionário. O cátodo emissor de electrões deixa o electrão e a parte frontal do tubo de vácuo atinge o electrão com o electrão no mesmo local. Por conseguinte, utilizamos a fórmula de dilatação temporal para relacionar o tempo adequado no quadro de repouso do electrão com o tempo no quadro de televisão.
Solução
- Identificar os conhecimentos (da parte a):
\
- Identificar o desconhecido: \(da parte a).
- Faz o cálculo:
\ &= 3,26 ^{-9}s vezes 10^{-9}s. \{{alinhamento*}]
Expressar a resposta como uma equação:
\
Significação
O tempo de viagem é mais curto no quadro electrónico de referência. Como o problema requer encontrar o intervalo de tempo medido em diferentes quadros de referência para o mesmo processo, a relatividade está envolvida. Se tivéssemos tentado calcular o tempo no quadro de repouso do electrão simplesmente dividindo os 0,200 m pela velocidade, o resultado seria ligeiramente incorrecto devido à velocidade relativista do electrão.
Exercicio \(\PageIndex{1})
p>O que é \PageIndex{1}p>O que é \PageIndex(v = 0.650c\)? Resposta
O Paradoxo do Gémeo
Uma consequência intrigante da dilatação do tempo é que um viajante espacial em movimento a alta velocidade em relação à Terra envelheceria menos do que o gémeo terrestre do astronauta. Isto é frequentemente conhecido como o paradoxo dos gémeos. Imagine-se o astronauta movendo-se a uma velocidade tal que o astronauta (gamma = 30,0), como na Figura 4). Uma viagem que leva 2,00 anos no seu quadro levaria 60,0 anos no quadro do gémeo terrestre. Suponhamos que o astronauta viaja 1,00 ano para outro sistema estelar, explora brevemente a área, e depois viaja 1,00 ano de volta. Um astronauta com 40 anos de idade no início da viagem teria 42 anos quando a nave espacial regressasse. Tudo na Terra, no entanto, teria 60,0 anos de idade. O gémeo terrestre, se ainda estivesse vivo, teria 100 anos.
A situação pareceria diferente da do astronauta da Figura \PageIndex{4}}. Como o movimento é relativo, a nave espacial pareceria estacionária e a Terra pareceria mover-se. (Esta é a sensação que se tem quando se voa num jacto.) Olhando pela janela da nave espacial, o astronauta veria o tempo abrandar na Terra por um factor de {\gamma = 30,0}. Visto da nave espacial, o irmão com destino à Terra teria apenas 2/30, ou 0,07, de um ano, enquanto que o astronauta teria 2,00 anos.
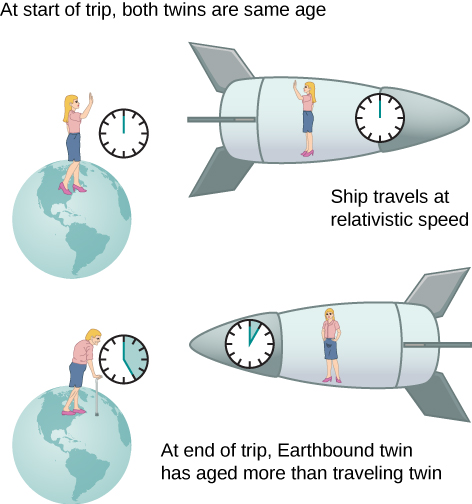
O paradoxo aqui é que os dois gémeos não podem estar ambos correctos. Como com todos os paradoxos, as conclusões contraditórias partem de uma falsa premissa. De facto, o movimento do astronauta é significativamente diferente do do gémeo terrestre. O astronauta acelera a uma velocidade elevada e depois desacelera para ver o sistema estelar. Para regressar à Terra, ela acelera e desacelera novamente. A nave espacial não se encontra num único quadro inercial ao qual a fórmula de dilatação temporal pode ser directamente aplicada. Ou seja, o astronauta gémeo muda as referências de inércia. O gémeo terrestre não sofre estas acelerações e permanece no mesmo quadro de inércia. Assim, a situação não é simétrica, e é incorrecto afirmar que o astronauta observa os mesmos efeitos que o seu gémeo. A falta de simetria entre os gémeos será ainda mais evidente quando analisarmos a viagem mais tarde neste capítulo em termos do caminho que o astronauta segue através do espaço-tempo tetradimensional.
Em 1971, os físicos americanos Joseph Hafele e Richard Keating verificaram a dilatação do tempo a baixas velocidades relativas ao voar em aviões comerciais com relógios atómicos extremamente precisos em todo o mundo. Mediram o tempo decorrido com uma precisão de alguns nanossegundos e compararam-no com o tempo medido pelos relógios deixados para trás. Os resultados de Hafele e Keating estavam dentro das incertezas experimentais das previsões de relatividade. Tanto a relatividade especial como a geral tiveram de ser tidas em conta, porque a gravidade e as acelerações estavam envolvidas, bem como o movimento relativo.
Exercicio \(\PageIndex{2A})
p>a. Uma partícula viaja a 1,90 vezes 10^8, m/s) e vive (2,1 vezes 10^8, s) quando em repouso em relação a um observador. Quanto tempo vive a partícula tal como vista em laboratório? Resposta
Exercício \(\PageIndex{2B})
p>p>Os veículos A e B passam em direcções opostas a uma velocidade relativa de \(4,00 ^7, m/s). Um relógio interno na nave A faz com que esta emita um sinal de rádio durante 1,00 s. O computador na nave B corrige o início e o fim do sinal depois de ter percorrido distâncias diferentes, para calcular o intervalo de tempo durante o qual a nave A estava a emitir o sinal. Qual é o intervalo de tempo que o computador na nave B calcula? Resposta
Apenas a velocidade relativa das duas naves espaciais importa porque não há movimento absoluto através do espaço. O sinal é emitido a partir de um local fixo no quadro de referência de A, pelo que o intervalo de tempo adequado da sua emissão é {\tau = 1,00, s}). A duração do sinal medido a partir do quadro de referência B é então
p>
Contribuidores e Atribuições
- p>Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs com muitos autores contribuintes. Esta obra é licenciada pela OpenStax University Physics sob uma Creative Commons Attribution License (by 4.0).