OBJECTIVOS DE APRENDIZAGEM
No final desta secção, será capaz de o fazer:
- Explicar o que é uma distribuição de carga de fonte contínua e como está relacionada com o conceito de quantização de carga
- Descrever cargas de linha, cargas de superfície e cargas de volume
- Calcular o campo de uma distribuição de carga de fonte contínua de qualquer sinal
As distribuições de carga que vimos até agora têm sido discretas: compostas de partículas pontuais individuais. Isto está em contraste com uma distribuição de carga contínua, que tem pelo menos uma dimensão não nula. Se uma distribuição de carga for contínua em vez de discreta, podemos generalizar a definição do campo eléctrico. Simplesmente dividimos a carga em peças infinitesimais e tratamos cada peça como uma carga pontual.
Nota que, porque a carga é quantizada, não existe uma distribuição de carga “verdadeiramente” contínua. No entanto, na maioria dos casos práticos, a carga total que cria o campo envolve um número tão grande de cargas discretas que podemos seguramente ignorar a natureza discreta da carga e considerá-la como contínua. Este é exactamente o tipo de aproximação que fazemos quando lidamos com um balde de água como um fluido contínuo, em vez de uma colecção de moléculas (H2O).
O nosso primeiro passo é definir uma densidade de carga para uma distribuição de carga ao longo de uma linha, através de uma superfície, ou dentro de um volume, como mostrado na Figura \PageIndex{1}}.
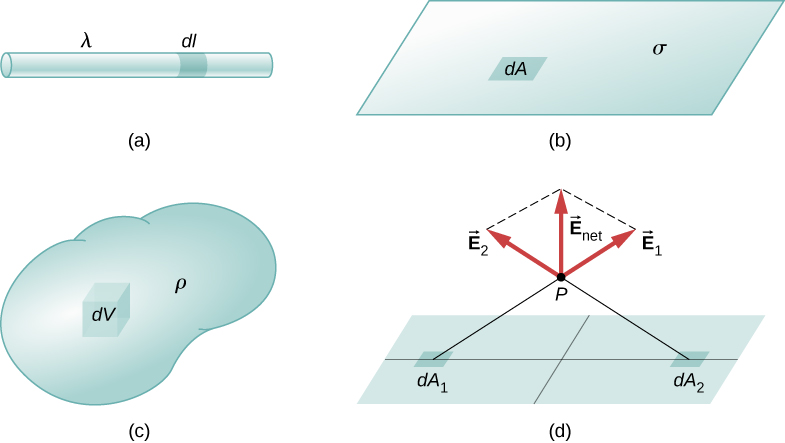
Definitions: Densidades de carga
Definições de densidade de carga:
- densidade de carga linear: \carga por unidade de comprimento (Figura 1a); unidades são coulombs por metro (C/m))
- densidade de carga de volume: \(Figura 1c)) carga por unidade de volume (Figura 1c)); unidades são coulombs por metro quadrado \((C/m^3)\)
densidade de carga superficial: \(Figura 1b)); unidades são coulombs por metro quadrado ((C/m^2)})
Para uma carga de linha, uma carga de superfície, e uma carga de volume, a soma na definição de um campo eléctrico discutida anteriormente torna-se integral e \(q_i\) é substituída por \(dq = lambda dl), \(\sigma dA\), ou \(rho dV\), respectivamente:
\vec{E}(P) &= {\i} {\i}{4\i}epsilon_0} \int_{line} \esquerda(esquerda(esquerda), dlambda, dl, direita) \etiqueta \\ ivec{E}(P) &= sobbrace{\i}{4\i}{4\i}epsilon_0} \int_{surface} \esquerda(fracracrac{sigma,dA}{r^2}{r^2}direita) que{r} }_{\text{Surface charge}}\label{eq3} \\ ivec{E}(P) &= sobbrace{\i}{4\i}{4\i}epsilon_0} \int_{volume} \esquerda(ffrac{rho,dV}{r^2}{r^2}{r^2}}_esquerda_esquerda_texto{cobra de volume}} \etiqueta \end{align}]
Os integrais em Equações {eq1}-ref{eq4} são generalizações da expressão para o campo de uma carga pontual. Incluem e assumem implicitamente o princípio da sobreposição. O “truque” para utilizá-los é quase sempre encontrar expressões correctas para {dl}, { dA}, ou {dV}, conforme o caso, expressas em termos de r, e também expressando adequadamente a função de densidade de carga. Pode ser constante; pode ser dependente da localização.
Nota cuidadosamente o significado de \(r\) nestas equações: É a distância do elemento de carga (q_i, lambda, dl, dl, sigma, dA, rho, dV)) ao local de interesse, (P(x, y, z)}) (o ponto no espaço onde se pretende determinar o campo). No entanto, não confunda isto com o significado de {r}; estamos a usá-lo e a notação vectorial para escrever três integrais de uma só vez. Ou seja, a equação {eq2} é na realidade
= E_y(P) &= ^dfrac{1}{4}pi ^epsilon_0} \int_{line} \esquerda, dl, dl, dl direita, E_z(P) &= |dfrac{1}{4pi |epsilon_0} \int_{line} \esquerda(ffrac, dlambda, dl, direita)_z, end, alinhar… \P>>div>p>exemplo {1}(PageIndex{1})): Campo Eléctrico de um Segmento de Linha
P>Cobrir o campo eléctrico a uma distância acima do ponto médio de um segmento de linha recta de comprimento que transporta uma densidade de carga de linha uniforme.
Estratégia
P>Porque esta é uma distribuição de carga contínua, partimos conceptualmente o segmento de fio em peças diferenciais de comprimento \(dl\), cada uma das quais transporta uma quantidade diferencial de carga
p>> Em seguida, calculamos o campo diferencial criado por duas peças simetricamente colocadas do fio, utilizando a simetria da configuração para simplificar o cálculo (Figura \PageIndex{2}). Finalmente, integramos esta expressão do campo diferencial ao longo do comprimento do fio (metade dele, na verdade, como explicamos abaixo) para obter a expressão completa do campo eléctrico.
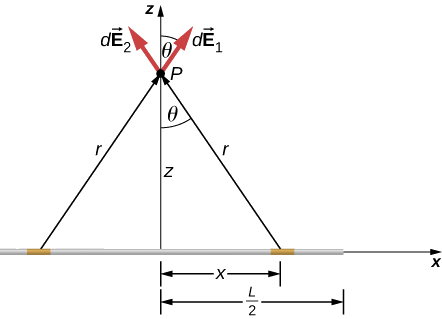
Solução
p>p> Antes de saltarmos para ele, como esperamos que o campo “se pareça” de longe? Uma vez que é um segmento de linha finito, de longe, deve parecer-se com uma carga pontual. Vamos verificar a expressão que obtemos para ver se corresponde a esta expectativa.
O campo eléctrico para uma carga de linha é dado pela expressão geral
>p>
A simetria da situação (a nossa escolha das duas peças diferenciais idênticas de carga) implica o cancelamento dos componentes horizontais (x) do campo, de modo a que o campo líquido aponte na direcção \(z). Vamos verificar isto formalmente.
O campo total {E}(P)} é a soma vectorial dos campos de cada um dos dois elementos de carga (chame-os {E}_1} e {E}_2}, por agora):
&= E_{1x}=hat{i} + E_{1z}}hat{k} + E_{2x} (- que{i}) + E_{2z} que{k}. \Fim{alinhamento*}]
p>Porque os dois elementos de carga são idênticos e estão à mesma distância do ponto em que queremos calcular o campo, { E_{1x} = E_{2x}), por isso esses componentes cancelam. Isto deixa
&= E_1, {\i1}, {\i}cc, {\i}theta {k}hat{\i} + E_2, E_2, E_2, E_2, E_2, E_2, E_2, E_2, E_2, E_2. \end{align*}]
Estes componentes também são iguais, por isso temos
&= ^dfrac{1}{4 ^pi ^epsilon_0}int_0^{L/2} ^dfrac{2=lambda dx}{r^2} \, custos, teta que \{alinhamento*}]
onde o nosso elemento de linha diferencial dl é dx, neste exemplo, uma vez que estamos a integrar ao longo de uma linha de carga que se situa no eixo x. (Os limites de integração são de 0 a {L2}, e não de 0 a {L2} a {2], porque construímos o campo líquido a partir de duas peças de carga diferencial dq]. Se nos integrássemos ao longo de todo o comprimento, detectaríamos um factor errado de 2.)
Em princípio, isto está completo. No entanto, para calcular realmente esta integral, precisamos de eliminar todas as variáveis que não são dadas. Neste caso, tanto as variáveis mudam à medida que nos integramos até ao fim da linha de carga, pelo que estas são as variáveis de que nos devemos livrar. Podemos fazer isso da mesma forma que fizemos para as cargas de dois pontos: notando que
e
>p>>p>Substituting, obtemos
\i>div id&= ^dfrac{1}{4 ^pi ^epsilon_0}int_0^{L/2} ^dfrac{2}{(z^2 + x^2)^{3/2}} dx ^hat{k} \\ {\i1}div id&= {2 lambda z}{4 {\i }epsilon_0} \esquerda_0^{L/2}hat{k}hat{k}. \{alinhamento*}]
o que simplifica a
p>>Significance
Nota, mais uma vez, o uso da simetria para simplificar o problema. Esta é uma estratégia muito comum para o cálculo de campos eléctricos. Os campos de distribuição de cargas não simétricas têm de ser tratados com vários integrais e podem precisar de ser calculados numericamente por um computador.
Exercicio \(\PageIndex{1})
p>Como é que a estratégia usada acima mudaria para calcular o campo eléctrico num ponto a uma distância \(z\) acima de uma extremidade do segmento de linha finita? Resposta
Não poderemos mais tirar partido da simetria. Em vez disso, teremos de calcular cada um dos dois componentes do campo eléctrico com o seu próprio integral.
Exemplo \(\PageIndex{2}}): Campo Eléctrico de uma Linha Infinita de Carga
P>Conhecer o campo eléctrico a uma distância acima do ponto médio de uma linha infinita de carga que transporta uma densidade de carga uniforme da linha {lambda}.
Estratégia
Isto é exactamente como o exemplo anterior, excepto que os limites de integração serão de { -infty} a { +infty}.
Solução
Ganho, os componentes horizontais cancelam, por isso acabamos com
p>>p>onde o nosso elemento de linha diferencial dl é dx, neste exemplo, uma vez que estamos a integrar ao longo de uma linha de carga que se situa no eixo x. Novamente,
\ &= \dfrac{z}{(z^2 + x^2)^{1/2}}. \end{align*} \]
Substituting, obtemos
\ &= \dfrac{1}{4 \pi \i \i}epsilon_0} \int_{-\infty}^{\infty} \dfrac{\i1}{(z^2 + x^2)^{3/2}dxhat{k} \\ {\i1}div id&
= {4 \i {\i}epsilon_0} \left_{-\infty}^{\infty} \o que \{alinhamento*}]
o que simplifica a
p>>Significação
A nossa estratégia de trabalho com distribuições de carga contínua também dá resultados úteis para cargas com dimensão infinita.
No caso de uma linha finita de carga, note-se que para { z ^gg L}, ^2} domina o L no denominador, de modo que a Equação {5}ref{5.12} simplifica para
p>>p> Se se lembrar que {\lambda L = q=) a carga total no fio, recuperámos a expressão para o campo de uma carga pontual, como esperado.
No limite {\i1}(L=lambda L = q=) por outro lado, obtemos o campo de um fio recto infinito, que é um fio recto cujo comprimento é muito, muito maior do que qualquer uma das suas outras dimensões, e também muito, muito maior do que a distância a que o campo deve ser calculado:
\\
Um artefacto interessante deste limite infinito é que perdemos a habitual dependência a que estamos habituados \(1/r^2\). Isto tornar-se-á ainda mais intrigante no caso de um plano infinito.
Exemplo \\(\PageIndex{3A}}): Campo eléctrico devido a um Anel de Carga
Um anel tem uma densidade de carga uniforme {lambda}, com unidades de coulomb por unidade de metro de arco. Encontrar o campo eléctrico num ponto do eixo que passa pelo centro do anel.
Estratégia
Usamos o mesmo procedimento que para o fio carregado. A diferença aqui é que a carga é distribuída sobre um círculo. Dividimos o círculo em elementos infinitesimais em forma de arcos no círculo e utilizamos as coordenadas polares mostradas na Figura \(\PageIndex{3}}.
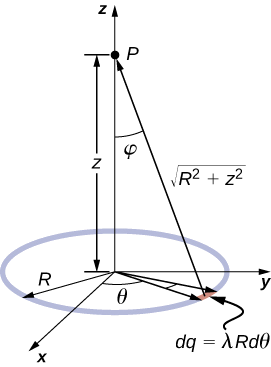
Solução
O campo eléctrico para uma carga de linha é dado pela expressão geral
pp>A O elemento geral do arco entre a lambda R e a dtheta + dtheta) é de comprimento (Rdtheta) e, portanto, contém uma carga igual à lambda R,d). O elemento está a uma distância de {z^2 + R^2}(r =sqrt{z^2 + R^2}), o ângulo é de {cos }, \phi = {z}{sqrt{z^2+R^2}} e portanto o campo eléctrico é
&
= ^dfrac{1}{4}pi ^epsilon_0} \ffrac{\i1}{(z^2 + R^2)^{3/2}}}{(z^2 + R^2)^{3/2}} \o que (z) \int_0^{2\pi} dtheta d&=dfrac{1}{4\pi {4\pi ^epsilon_0} \dfrac{2}{(z^2 + R^2)^{3/2}}{(z^2 + R^2)^{3/2}} \o que (z) \\ {4\i} &= dfrac{1}{4\i }epsilon_0} \^dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}}}{(z^2 + R^2)^{3/2}} \que{z}. \{z}]
Significação
Como de costume, a simetria simplificou este problema, neste caso particular resultando num integral trivial. Além disso, quando tomamos o limite de \\(z \gg R\), descobrimos que
como esperamos.
Exemplo \(\PageIndex{3B}}): O Campo de um Disco
Encontrar o campo eléctrico de um disco circular fino de raio \(R) e densidade de carga uniforme a uma distância \(z) acima do centro do disco (Figura \PageIndex{4}})
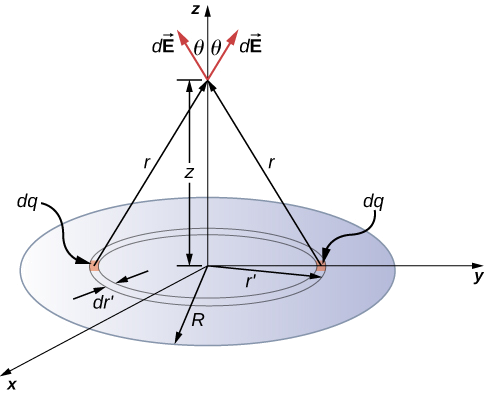
Estratégia
O campo eléctrico para uma carga de superfície é dado por
p>>p> Para resolver problemas de carga de superfície, quebramos a superfície em “faixas” diferenciais simétricas que correspondem à forma da superfície; aqui, usaremos anéis, como mostra a figura. Mais uma vez, por simetria, os componentes horizontais cancelam e o campo está inteiramente na direcção vertical ((k}){k}). A componente vertical do campo eléctrico é extraída multiplicando por \\\(\theta), por isso
>p>>p>Como antes, precisamos de reescrever os factores desconhecidos na integração e em termos das quantidades dadas. Neste caso,
p>
/p>
/p>p>(Por favor, tome nota dos dois “r” diferentes aqui; r(r) é a distância do anel diferencial de carga até ao ponto em que desejamos determinar o campo, enquanto que r(r’}) é a distância do centro do disco até ao anel diferencial de carga). Além disso, já realizámos a integral do ângulo polar por escrito \(dA\).
Solução
Substituindo tudo isto, obtemos
\ &= \dfrac{1}{4 \pi \pi \epsilon_0} \int_0^R ^R ^dfrac{\i r’ dr’)z}{(r’^2 + z^2)^{3/2}}}{(r’^2 + z^2)^{3/2}} \o que (k) \\ {\i1}div id&
= {4 \i {\i}epsilon_0} (2\pi ^sigma z)esquerda(1}{z} – ^dfrac{1}{1}{sqrt{R^2 + z^2}}direita) {k}hat{k} \P>P>p>ou, mais simplesmente,p>p>>p>P>Significancep>p>Again, pode ser mostrado (através de uma expansão de Taylor) que, quando se reduz ap>p>p>p>p>p>p> que é a expressão para uma carga de ponto { Q = ^2^pi R^2}).
Exercicio \\(\PageIndex{3})
Como mudaria o limite acima com um rectângulo uniformemente carregado em vez de um disco?
Resposta
A carga de ponto seria {Q = ^sigma ab} onde {a} e {b} são os lados do rectângulo, mas de resto idênticos.
As {R-rightarrow {infty}), Equação Ref{5.14} reduz-se ao campo de um plano infinito, que é uma folha plana cuja área é muito, muito maior do que a sua espessura, e também muito, muito maior do que a distância a que o campo deve ser calculado:
\i>div id&= \dfrac{\sigma}{2 \epsilon_0} \o que (k). \rótulo{5.15} \Fim de linha de campo Este resultado surpreendente é, mais uma vez, um artefacto do nosso limite, embora um que faremos uso repetidamente no futuro. Para compreender por que razão isto acontece, imagine ser colocado acima de um plano infinito de carga constante. Será que o avião tem um aspecto diferente se variar a sua altitude? Não, ainda se vê o avião a descolar para o infinito, por muito longe que se esteja dele. É importante notar que a Equação \ref{5.15} é porque estamos acima do avião. Se estivéssemos abaixo, o campo apontaria na direcção {k}(-hat{k}).
Exemplo {4}(PageIndex{4}): O Campo de Dois Planos Infinitos
Encontrar o campo eléctrico em todo o lado resultante de dois planos infinitos com densidades de carga iguais mas opostas (Figura \PageIndex{5}).
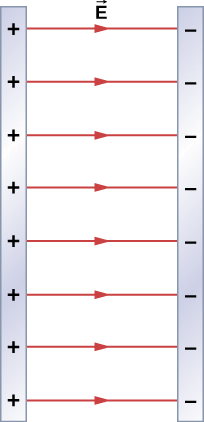
Estratégia
Já conhecemos o campo eléctrico resultante de um único plano infinito, pelo que podemos utilizar o princípio da sobreposição para encontrar o campo de dois.
Solução
O campo eléctrico aponta para longe do plano com carga positiva e para o plano com carga negativa. Uma vez que o \sigma é igual e oposto, isto significa que na região fora dos dois planos, os campos eléctricos cancelam-se mutuamente até zero. Contudo, na região entre os planos, os campos eléctricos acrescentam, e obtemos
para o campo eléctrico. O {i}(que é o que se obtém) é porque na figura, o campo aponta na direcção +x.
Significado
Sistemas que podem ser aproximados como dois planos infinitos deste tipo proporcionam um meio útil de criar campos eléctricos uniformes.
Exercicio \(\PageIndex{4})
Como seria o campo eléctrico num sistema com dois planos paralelos de carga positiva com densidades de carga iguais?
Resposta
O campo eléctrico seria zero no meio, e teria magnitude {\i}{\i1}(ffrac{\i}{\i1}epsilon_0} em qualquer outro lugar.
Contribuidores e Atribuições
- p>Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs com muitos autores contribuintes. Esta obra é licenciada pela OpenStax University Physics sob uma licença Creative Commons Attribution License (por 4.0).