
Num artigo anterior, explorámos a Análise de Regressão Linear e a sua aplicação na análise financeira e modelação. Pode ler o nosso artigo Análise de Regressão na Modelação Financeira para obter mais informações sobre os conceitos estatísticos empregues no método e onde encontra aplicação dentro das finanças.
Este artigo irá dar uma olhada prática à modelação de um modelo de Regressão Múltipla para o Produto Interno Bruto (PIB) de um país.
Antes de começar, deixe-me acrescentar uma breve declaração de exoneração de responsabilidade. Não sou um estatístico, e não pretendo que as variáveis dependentes e independentes seleccionadas sejam as escolhas de análise correctas. O artigo visa mostrar como executar Regressão múltipla em Excel e interpretar os resultados, e não ensinar a estabelecer os nossos pressupostos de modelo e a escolher as variáveis mais apropriadas.
Agora que isto esteja fora do caminho e que as expectativas estejam estabelecidas, vamos abrir o Excel e começar!
Obteremos dados públicos do Eurostat, a base de dados estatísticos para a Comissão Europeia para este exercício. Todos os dados de fonte relevantes estão dentro do ficheiro modelo para sua conveniência, que pode descarregar abaixo. Também mantive os links para as tabelas de fontes para explorar mais se quiser.
O conjunto de dados da UE dá-nos informações para todos os estados membros da união. Como grande fã de Agatha Christie’s Hercule Poirot, vamos dirigir a nossa atenção para a Bélgica.
Como pode ver na tabela abaixo, temos dezanove observações da nossa variável alvo (PIB), bem como as nossas três variáveis preditoras:
- X1 – Gastos com educação em mil.;
li>X2 – Taxa de desemprego como % da Força de Trabalho;li>X3 – Remuneração dos empregados em mil.

Even antes de executarmos o nosso modelo de regressão, notamos algumas dependências nos nossos dados. Olhando para o desenvolvimento ao longo dos períodos, podemos assumir que o PIB aumenta juntamente com as despesas de Educação e Remuneração de Funcionários.
Executar uma Regressão Linear Múltipla
Existem formas de calcular todas as estatísticas relevantes em Excel utilizando fórmulas. Mas é muito mais fácil com o Pacote de Ferramentas de Análise de Dados, que pode activar a partir do separador Desenvolvedor ->Adicionamento Excel.
Localize o separador Dados, e à direita, verá a ferramenta de Análise de Dados dentro da secção Análise.
Executar e escolher Regressão a partir de todas as opções. Nota, utilizamos o mesmo menu tanto para modelos de regressão linear simples (simples) como múltiplos.
P>Agora é altura de definir alguns intervalos e configurações.
A Intervalo Y incluirá a nossa variável dependente, PIB. E na Gama X, iremos seleccionar todas as colunas de X variáveis. Por favor, note que isto é o mesmo que executar uma única regressão linear, a única diferença é que escolhemos várias colunas para o Gama X.
Lembrem-se que o Excel requer que todas as variáveis X estejam em colunas adjacentes.
Como seleccionei os Títulos das colunas, é crucial marcar a caixa de verificação para os Rótulos. Um intervalo de confiança de 95% é apropriado na maioria dos cenários de análise financeira, pelo que não alteraremos isto.
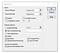
P>Pode então considerar a colocação dos dados na mesma folha ou numa nova. Uma nova folha de trabalho geralmente funciona melhor, uma vez que a ferramenta insere uma grande quantidade de dados.
Eu também marcarei todas as opções adicionais na parte inferior. Raramente acabo por utilizar todas elas, mas é mais fácil apagar as que não precisamos do que voltar a executar tudo de novo.
p>Junte-se à nossa Newsletter para um Modelo de Análise de Benchmark Excel GRÁTIS
Avaliação dos Resultados da Regressão
Agora temos o nosso Resumo de Resultados do Excel vamos explorar melhor o nosso modelo de regressão.
A informação que obtivemos do módulo de Análise de Dados do Excel começa com as Estatísticas de Regressão.
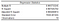
quadrado R é o mais importante de todos, para que possamos começar por olhar para ela. Especificamente, devemos olhar para a Praça R Ajustada no nosso caso, uma vez que temos mais de uma variável X. Dá-nos uma ideia da bondade geral do ajuste.
Um quadrado R ajustado de 0,98 significa que o nosso modelo de regressão pode explicar cerca de 98% da variação da variável dependente Y (PIB) em torno do valor médio das observações (a média da nossa amostra). Por outras palavras, 98% da variabilidade em ŷ (y-hat, as nossas previsões da variável dependente) é captada pelo nosso modelo. Um valor tão elevado indicaria normalmente que poderia haver algum problema com o nosso modelo. Vamos continuar com o nosso modelo, mas um R Squared demasiado elevado pode ser problemático num cenário da vida real. Sugiro que leia este artigo sobre Estatísticas de Jim, para saber por que razão nem sempre é bom demais em termos de R Quadrado.
O erro padrão dá-nos uma estimativa do desvio padrão do erro (resíduos). Geralmente, se o coeficiente for grande em comparação com o erro padrão, é provavelmente estatisticamente significativo.
Análise de Variância (ANOVA)

A secção Análise de Variância é algo que muitas vezes saltamos quando modelamos a Regressão. No entanto, pode fornecer valiosos insights, e vale a pena dar uma vista de olhos. Pode ler mais sobre a execução de um teste ANOVA e ver um modelo exemplo no nosso artigo dedicado.
Esta tabela dá-nos um teste global de significância sobre os parâmetros de regressão.
A coluna F da tabela ANOVA dá-nos o teste F global da hipótese nula de que todos os coeficientes são iguais a zero. A hipótese alternativa é de que pelo menos um dos coeficientes não é igual a zero. A coluna Significância F mostra-nos o valor p para o teste F. Como é inferior ao nível de significância de 0,05 (ao nosso nível de confiança escolhido de 95%), podemos rejeitar a hipótese nula, de que todos os coeficientes são iguais a zero. Isto significa que os nossos parâmetros de regressão não são em conjunto estatisticamente insignificantes.
P>Pode ler mais sobre o teste de Hipótese no nosso artigo dedicado.
A tabela seguinte dá-nos informações sobre os coeficientes no nosso Modelo de Regressão Múltipla e é a parte mais excitante da análise.

Aqui temos muitos detalhes para a intercepção e cada um dos nossos preditores (variáveis independentes). Vamos explorar o que estas colunas representam:
- Coeficientes – estas são estimativas derivadas pelo método dos mínimos quadrados;
- Erro padrão – o desvio padrão das estimativas dos mínimos quadrados;
- T-Stat – esta é a estatística t para a hipótese nula de que o coeficiente é igual a zero, versus a hipótese alternativa de que é diferente de zero;
- O valor P para o teste t;
- Li>Baixo e Alto 95% definem o intervalo de confiança para os coeficientes.
Teste de significância estatística
Este é o teste de uma hipótese nula que declara que o coeficiente tem um declive de zero. Podemos olhar para os valores p de cada coeficiente e compará-los com o nível de significância de 0,05.
Se o nosso valor p for inferior ao nível de significância, isto significa que a nossa variável independente é estatisticamente significativa para o modelo. Olhando para os nossos preditores X1 a X3, notamos que apenas X3 Remuneração do Empregado tem um valor p inferior a 0,05, o que significa que X1 Gastos com educação e X2 Taxa de desemprego não parecem ser estatisticamente significativos para o nosso modelo de regressão.
Como não podemos rejeitar a hipótese nula (que os coeficientes são iguais a zero), podemos eliminar X1 e X2 do modelo. Podemos também confirmar isto porque o valor zero situa-se entre os parênteses de confiança inferior e superior.
Podemos decidir executar o modelo sem as variáveis X1 e X2 e avaliar se isto resulta numa queda significativa na medida ajustada do quadrado R. Se não resultar, então é seguro largar X1 e X2 do modelo de regressão.
Se o fizermos, obtemos as seguintes Estatísticas de Regressão.

Não podemos ver queda no R Quadrado, para que possamos remover com segurança X1 e X2 do nosso modelo e simplificá-lo para uma única regressão linear.
Residual Output
Os resíduos dão informações sobre até que ponto os pontos de dados reais (y) se desviam dos pontos de dados previstos (ŷ), com base no nosso modelo de regressão.

Probability Output
Esta tabela mostra os valores observados para a variável independente (y) e os percentis de amostra correspondentes. Podemos calcular o primeiro percentil como (100 / 2 * Número de observações), e a partir daí, estes são calculados como o percentil anterior + (100 / 2).

LotesResiduais
A análise de Regressão Múltipla dá-nos um lote para cada variável independente versus os resíduos. Podemos utilizar estas parcelas para avaliar se os nossos dados de amostra se ajustam às hipóteses de linearidade e homogeneidade da variância.
Homogeneidade significa que a parcela deve apresentar um padrão aleatório e ter uma propagação vertical constante.
Linearidade requer que os resíduos tenham uma média de zero. Podemos observar isto visualmente, avaliando se os pontos estão espalhados aproximadamente igualmente abaixo e acima do eixo x.



Line Fit Plots
O modelo fornece-nos um Line Fit Plot para cada variável independente (preditor). Isto mostra os valores previstos (ŷ) versus os valores observados (y). Quanto mais próximos estes corresponderem, melhor o nosso modelo prevê a variável dependente com base nos regressores.


/div>

/div>
Plote de Probabilidade Normal
O Plot de Probabilidade Normal ajuda-nos a determinar se os dados se ajustam a uma distribuição normal. Podemos adicionar uma linha de tendência e avaliar se os pontos de dados seguem uma linha recta. No nosso caso, isto é bastante óbvio, e podemos até não adicionar a linha de tendência.

P>Pode descarregar o modelo de exemplo em Excel no artigo original.
Excel Limitações
Como o Excel não é um software estatístico especializado, existem algumas limitações inerentes à execução de um modelo de regressão que devemos estar cientes:
- As colunas para todos os regressores (variáveis independentes) têm de ser adjacentes;
- Podemos ter até 16 preditores (não me lembro onde li isso, por isso tomem-no com cautela);
- A análise de regressão em Excel assume que o erro é independente com variância constante (homoskedasticidade);
- Se seguirmos a rota das funções, é crucial saber que as funções SLOPE, INTERCEPT, e FORECAST do Excel não funcionam para Regressão Múltipla. Em contraste, TREND e LINEST funcionam da mesma forma que com um único modelo de regressão mas tomam valores para múltiplas variáveis X.
Conclusion
Iniciamos com três variáveis independentes, efectuámos uma análise de regressão, e identificámos que dois preditores não têm significado estatístico para o nosso modelo.
Após eliminámos aqueles que acabaram com um modelo de Regressão Linear Única.
Após estar satisfeito com o seu modelo, pode construir a sua equação de regressão, como discutimos noutros artigos. Com esta equação poderá então prever a variável dependente para o futuro.
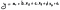
/div>>
p>Onde:
- y é a nossa variável dependente;
- a é a intercepção (a nossa constante) das estatísticas de regressão;
- b, c, e d são os coeficientes para cada variável;
- ɛ é o erro ou resíduo, que podemos frequentemente excluir.
li>x1 a x3 são as variáveis independentes (os nossos regressores ou preditores);
Keep, tendo em mente que este artigo pretende ilustrar os conceitos de execução de uma Análise de Regressão Múltipla em Excel. Tenta explicar em que nos devemos concentrar ao avaliar os resultados. Cada bom modelo começa com o estabelecimento de suposições e expectativas razoáveis, nas quais não sou especialista, pelo que não faço alegações de que as variáveis dependentes e independentes escolhidas foram as escolhas certas.
P>Obrigado pela leitura! Pode mostrar o seu apoio partilhando este artigo com colegas e amigos.