Show Mobile Notice Show All Notes Hide All Notes
Secção 1-12 : Coordenadas cilíndricas
As com espaço bidimensional o sistema de coordenadas padrão \(esquerda( {x,y,z} {direita)}) é chamado sistema de coordenadas cartesianas. Nas duas últimas secções deste capítulo, vamos analisar alguns sistemas de coordenadas alternativas para o espaço tridimensional.
Começaremos com o sistema de coordenadas cilíndrico. Este é bastante simples, pois nada mais é do que uma extensão de coordenadas polares em três dimensões. Não só é uma extensão de coordenadas polares, como também o estendemos para a terceira dimensão, tal como estendemos as coordenadas cartesianas para a terceira dimensão. Tudo o que fazemos é acrescentar um {\i1}(z) como a terceira coordenada. O {\i1}(r) e o {\i1}theta} são os mesmos que com as coordenadas polares.
Aqui está um esboço de um ponto em {\i1}(r}mathbb{R}^3}).
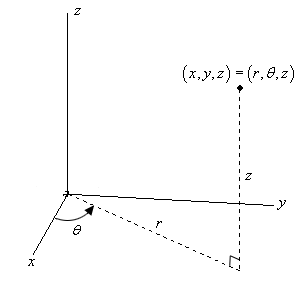
As conversões para \(x) e \(y) são as mesmas conversões que utilizámos quando olhávamos para as coordenadas polares. Assim, se tivermos um ponto em coordenadas cilíndricas, as coordenadas cartesianas podem ser encontradas utilizando as seguintes conversões.
A terceira equação é apenas um reconhecimento de que a coordenada \(z)-de um ponto em coordenadas cartesianas e polares é a mesma.
Likewise, se tivermos um ponto em coordenadas cartesianas as coordenadas cilíndricas podem ser encontradas utilizando as seguintes conversões.
Vejamos rapidamente algumas superfícies em coordenadas cilíndricas.
- \(r = 5\)
- \({r^2} + {z^2} = 100\)
- \(z = r\)
Mostrar todas as soluções Esconder todas as soluções
Em duas dimensões sabemos que se trata de um círculo de raio 5. Uma vez que agora estamos em três dimensões e não há \\(z) na equação, isto significa que é permitido variar livremente. Assim, para qualquer dado, teremos um círculo de raio 5 centrado no eixo {z} -p>> Por outras palavras, teremos um cilindro de raio 5 centrado no eixo {z} -p.
b \\({r^2} + {z^2} = 100\) Mostrar Solução
Esta equação será fácil de identificar uma vez que convertemos de volta para coordenadas cartesianas.
\\
Então, esta é uma esfera centrada na origem com raio 10.
c \(z = r\) Mostrar Solução
Again, esta não será muito má se nos convertermos de volta para cartesianas. Por razões que acabarão por ser aparentes, vamos primeiro esquadrinhar ambos os lados, depois converter.
\
Da secção sobre superfícies quadriculadas sabemos que esta é a equação de um cone.