- Comportamento da Média da Amostra (x-bar)
- Distribuição da Média da Amostragem
Comportamento da Média da Amostra (x-bar)
Até agora, discutimos o comportamento da estatística p-hat, a proporção da amostra, relativamente ao parâmetro p, a proporção da população (quando a variável de interesse é categórica).
Agora vamos explorar o comportamento da barra-x estatística, a média da amostra, relativamente ao parâmetro μ (mu), a média da população (quando a variável de interesse é quantitativa).
P>Comecemos com um exemplo.
EXEMPLO 9: Comportamento da Amostra Meios
Pesos de nascimento são registados para todos os bebés de uma cidade. O peso médio de nascimento é de 3.500 gramas, µ = mu = 3.500 g. Se recolhermos muitas amostras aleatórias de 9 bebés de cada vez, como acha que se comportarão os meios de amostra?
Aqui novamente, estamos a trabalhar com uma variável aleatória, uma vez que as amostras aleatórias terão meios que variam imprevisivelmente a curto prazo, mas exibem padrões a longo prazo.
Baseado na nossa intuição e no que aprendemos sobre o comportamento das proporções da amostra, podemos esperar o seguinte sobre a distribuição de meios de amostra:
Centro: Alguns meios de amostra estarão no lado baixo – digamos 3.000 gramas ou mais – enquanto outros estarão no lado alto – digamos 4.000 gramas ou mais. Na amostragem repetida, é de esperar que as amostras aleatórias se situem na média da média da população subjacente de 3.500 g. Por outras palavras, a média da média da amostra será µ (mu), tal como a média das proporções da amostra foi p.
Spread: Para amostras grandes, podemos esperar que os meios de amostra não se afastem demasiado da média da população de 3.500 g. A amostra significa menos de 3.000 ou mais de 4.000 pode ser surpreendente. Para amostras mais pequenas, seríamos menos surpreendidos por meios de amostra que variavam bastante entre 3.500. Por outras palavras, poderíamos esperar uma maior variabilidade nos meios de amostra para amostras mais pequenas. Assim, o tamanho da amostra desempenhará novamente um papel na propagação da distribuição das medidas da amostra, tal como observámos para as proporções da amostra.
Forma: Os meios de amostra mais próximos de 3.500 serão os mais comuns, com os meios de amostra longe de 3.500 em qualquer direcção progressivamente menos prováveis. Por outras palavras, a forma da distribuição dos meios da amostra deve ser a mais proeminente no meio e cónica nas extremidades, com uma forma que seja um pouco normal. Isto, mais uma vez, foi o que vimos quando olhámos para as proporções da amostra.
Comentário:
- A distribuição dos valores da média da amostra (x-bar) em amostras repetidas chama-se a distribuição da amostra de x-bar.
p> Vamos olhar para uma simulação:
Consegui isto? Simulação #3 (x-bar)
Os resultados que encontramos nas nossas simulações não são surpreendentes. A teoria avançada da probabilidade confirma que ao afirmar o seguinte:
A Distribuição da Média da Amostragem
Se amostras aleatórias repetidas de um determinado tamanho n forem retiradas de uma população de valores para uma variável quantitativa, onde a média da população é μ (mu) e o desvio padrão da população é σ (sigma) então a média de todas as médias da amostra (x-bars) é a média da população μ (mu).
Como para a dispersão de todas as médias de amostra, a teoria dita o comportamento muito mais precisamente do que dizer que há menos dispersão para amostras maiores. Na realidade, o desvio padrão de todos os meios de amostra está directamente relacionado com o tamanho da amostra, n como indicado abaixo.
![]()
Desde que a raiz quadrada do tamanho da amostra n aparece no denominador, o desvio padrão diminui à medida que o tamanho da amostra aumenta.
Aprender Fazendo: Distribuição de Amostragem (barra x)
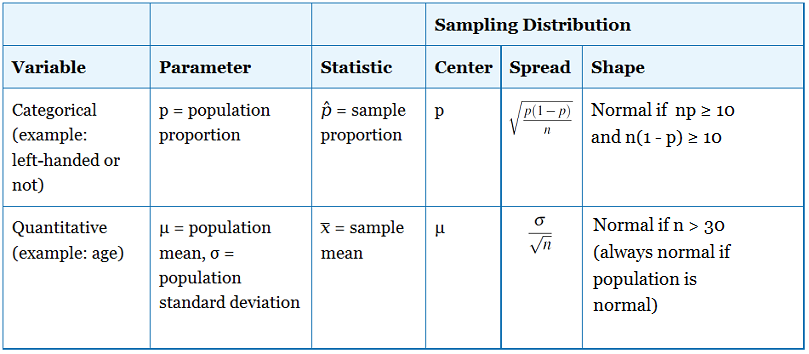
Vamos comparar e contrastar o que sabemos agora sobre as distribuições de amostra para as médias e proporções da amostra.

Agora vamos investigar a forma da distribuição de amostra das médias de amostra. Quando estávamos a discutir a distribuição das proporções das amostras, dissemos que esta distribuição é aproximadamente normal se np ≥ 10 e n(1 – p) ≥ 10. Por outras palavras, tínhamos uma orientação baseada no tamanho da amostra para determinar as condições sob as quais poderíamos utilizar cálculos de probabilidade normais para as proporções da amostra.
Quando é que a distribuição de meios de amostra será aproximadamente normal? Isto depende do tamanho da amostra?
Parece razoável que uma população com uma distribuição normal tenha meios de amostra que são normalmente distribuídos mesmo para amostras muito pequenas. Vimos isto ilustrado na simulação anterior com amostras de tamanho 10,
O que acontece se a distribuição da variável na população for fortemente enviesada? Os meios de amostra também têm uma distribuição enviesada? Se recolhermos amostras realmente grandes, os meios de amostra tornar-se-ão mais normalmente distribuídos?
Na próxima simulação, investigaremos estas questões.
Consegui isto? Simulação #4 (x-bar)
Para resumir, a distribuição de meios de amostra será aproximadamente normal desde que o tamanho da amostra seja suficientemente grande. Esta descoberta é provavelmente o resultado mais importante apresentado nos cursos de estatística introdutória. É declarado formalmente como o Teorema do Limite Central.
dependeremos do Teorema do Limite Central uma e outra vez para fazer cálculos normais de probabilidade quando utilizamos meios de amostra para tirar conclusões sobre uma média populacional. Sabemos agora que podemos fazer isto mesmo que a distribuição da população não seja normal.
Quanto tamanho de amostra precisamos para assumir que os meios de amostra serão normalmente distribuídos? Bem, depende realmente da distribuição da população, como vimos na simulação. A regra geral é que as amostras de tamanho 30 ou superior terão uma distribuição bastante normal independentemente da forma da distribuição da variável na população.
Applet: Distribuição de Amostragem para uma Média de Amostra
Comentário:
- Para variáveis categóricas, a nossa alegação de que as proporções de amostra são aproximadamente normais para n suficientemente grandes é na realidade um caso especial do Teorema do Limite Central. Neste caso, pensamos nos dados como 0’s e 1’s e a “média” destes 0’s e 1’s é igual à proporção que discutimos.
Antes de trabalharmos alguns exemplos, vamos comparar e contrastar o que sabemos agora sobre as distribuições de amostras para as médias e proporções da amostra.
EXEMPLO 10: Usando a Distribuição de Amostragem de x-bar
Tamanho de casa nos Estados Unidos da América tem uma média de 2,6 pessoas e desvio padrão de 1,4 pessoas. Deve ficar claro que esta distribuição é enviesada para a direita, uma vez que o menor valor possível é um agregado familiar de 1 pessoa, mas os agregados familiares maiores podem ser de facto muito grandes.
(a) Qual é a probabilidade de um agregado familiar escolhido aleatoriamente ter mais de 3 pessoas?
Uma aproximação normal não deve ser usada aqui, porque a distribuição do tamanho do agregado familiar seria consideravelmente enviesada para a direita. Não temos informação suficiente para resolver este problema.
(b) Qual é a probabilidade de o tamanho médio de uma amostra aleatória de 10 agregados familiares ser superior a 3?
Pelos padrões de qualquer pessoa, 10 é um tamanho de amostra pequeno. O Teorema do Limite Central não garante que a média da amostra proveniente de uma população enviesada seja aproximadamente normal, a menos que o tamanho da amostra seja grande.
(c) Qual é a probabilidade de o tamanho médio de uma amostra aleatória de 100 agregados familiares ser superior a 3?
Agora podemos invocar o Teorema do Limite Central: mesmo que a distribuição do tamanho do agregado familiar X seja enviesada, a distribuição do tamanho médio da amostra (barra x) é aproximadamente normal para um tamanho de amostra grande como 100. A sua média é a mesma que a média da população, 2.6, e o seu desvio padrão é o desvio padrão da população dividido pela raiz quadrada do tamanho da amostra:

para encontrar
![]()
normalizamos 3 para um z-score, subtraindo a média e dividindo o resultado pelo desvio padrão (da média da amostra). Depois podemos encontrar a probabilidade usando a calculadora ou tabela normal.

Households of more than 3 people are, course, quite common, but it would be extremely unusual for the mean size of a sample of 100 households to be more than 3.
O objectivo da actividade seguinte é dar uma prática orientada na procura da distribuição da média da amostra (x-bar), e usá-la para aprender sobre a probabilidade de obter certos valores de x-bar.
Aprender Fazendo: Usando a distribuição de amostras de x-bar #2 Consegui isto? Usando a Distribuição de Amostragem de x-bar