Mecânica dos Materiais
Shear Equações de Tensão de Cisalhamento e Aplicações
Tensão de Cisalhamento Geral:
A fórmula para calcular a tensão de cisalhamento média é
onde τ = a tensão de cisalhamento; F = a força aplicada; A = a área da secção transversal do material com área perpendicular ao vector de força aplicada;
Cisalhamento de viga:
Cisalhamento de viga é definido como a tensão de cisalhamento interno de uma viga causada pela força de cisalhamento aplicada à viga.
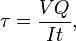onde V = força de corte total no local em questão; Q = momento estático da área; t = espessura no material perpendicular ao corte; I = momento de inércia de toda a área da secção transversal. Esta fórmula é também conhecida como a fórmula de Jourawski. As tensões de cisalhamento semi-monocrocoShear dentro de uma estrutura semi-monocroca podem ser calculadas através da idealização da secção transversal da estrutura num conjunto de cordas (transportando apenas cargas axiais) e teias (transportando apenas fluxos de cisalhamento). A divisão do fluxo de cisalhamento pela espessura de uma determinada porção da estrutura semi-monocoque produz a tensão de cisalhamento. Assim, a tensão de cisalhamento máxima ocorrerá quer na teia de fluxo de cisalhamento máximo, quer na espessura mínima, o peso de uma barragem ou dique cheio de terra pode causar o colapso do subsolo, como um pequeno deslizamento de terra.Cisalhamento de impactoA tensão máxima de cisalhamento criada numa barra redonda sólida sujeita a impacto é dada como a equação:
onde U = alteração da energia cinética; G = módulo de cisalhamento; V = volume da barra; e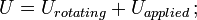 
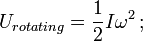
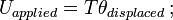
= momento de inércia da massa; ω = velocidade angular.
Tensão de corte em fluidos:
Um qualquer fluido real (líquidos e gases incluídos) em movimento ao longo de um limite sólido incorrerá numa tensão de corte nesse limite. A condição de não deslizamento dita que a velocidade do fluido no limite (relativamente ao limite) é zero, mas a alguma altura do limite a velocidade do fluxo deve ser igual à do fluido. A região entre estes dois pontos é apropriadamente denominada camada limite. Para todos os fluidos newtonianos em fluxo laminar, a tensão de corte é proporcional à taxa de deformação no fluido onde a viscosidade é a constante de proporcionalidade. Contudo, para os fluidos não Newtonianos, este já não é o caso, pois para estes fluidos a viscosidade não é constante. A tensão de cisalhamento é transmitida para o limite como resultado desta perda de velocidade. A tensão de cisalhamento, para um fluido Newtoniano, num elemento de superfície paralelo a uma placa plana, no ponto y, é dada por:
onde μ é a viscosidade dinâmica do fluido; u é a velocidade do fluido ao longo do limite; y é a altura acima do limite. Especificamente, a tensão de cisalhamento da parede é definida como: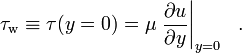 
Em caso de vento, a tensão de cisalhamento no limite é chamada tensão de vento.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Dia, Michael A. (2004), The noslip condition of fluid dynamics, Springer Netherlands, pp. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.Reynolds, W. C. (jan 1987), “Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Relatório Técnico N 87
4. Große, S.; Schröder, W. (2009), “Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars”, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), “Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³”, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008