A transformação de Fourier (FT) decompõe um sinal nas frequências que a compõem.
O que significa isto?
Então, vamos tomar um exemplo. Vamos ter um sinal S1.

/div>
se quisermos medir a força deste sinal em algum momento específico. Medimo-la pela sua amplitude.
Assim, a amplitude do sinal S1 é 1
Se fizermos o mesmo para outro sinal e seleccionarmos o mesmo momento no tempo e medirmos a sua amplitude. Vamos ter outro sinal S2 como este

>/div>>>>S2: x-eixo é tempo e o eixo y é amplitude
também, a amplitude do sinal S2 é 2
Agora, o que acontece quando emitimos estes dois sinais ao mesmo tempo (S1 e S2) ?
Então, quando emitimos estes dois sinais ao mesmo tempo, obtemos um novo sinal que é a soma da amplitude destes dois sinais. Isto é assim porque estes dois sinais estão a ser somados.

So, a amplitude de S3 = amplitude de S1 + amplitude de S2 = 1 + 2 = 3
Então, a amplitude do sinal S3 é 3
Agora, a questão interessante é :
Se nos for dado apenas o sinal S3 (que é a soma dos sinais S1 e S2).Podemos recuperar os sinais originais S1 e S2?
Sim. É o que faz uma transformada de Fourier. Ela pega num sinal e decompõe-o nas frequências que o compõem.
No nosso exemplo, uma transformada de Fourier decomporia o sinal S3 nas suas frequências constituintes como os sinais S1 e S2
Mas, como podemos recuperar os sinais originais? O que fará a transformação de Fourier por nós?

Deixe que os três sinais da imagem acima sejam S1, S2, e S3 e quando fundimos estes três sinais, obtemos o sinal em Vermelho que é na realidade a soma dos três sinais S1+S2+S3.
O que a transformada de Fourier faz é que nos move do domínio do tempo para o domínio da frequência.
No caso de alguém se interrogar, E se quisermos voltar do domínio da frequência para o domínio do tempo ?
Podemos fazê-lo utilizando a transformada de Fourier Inversa(IFT). Mas não vamos discutir isto neste artigo.
Signal Generation and Phase Shift
Se quisermos descrever um sinal, precisamos de três coisas :
- A frequência do sinal que mostra, quantas ocorrências no período que temos.
- Amplitude que mostra a altura do sinal ou em outros termos a força do sinal.
- Phase shift as to where does the signal starts.
O primeiro exemplo que tomámos foi muito simples, cada sinal tinha a mesma frequência e diferença de fase e apenas amplitudes diferentes.
Vamos agora olhar para um exemplo ligeiramente complexo e vamos olhar para o sinal individual do exemplo acima porque para compreender melhor a transformação de Fourier precisamos de olhar para os sinais individuais de perto.
Below são os sinais originais que estávamos a ver acima.



Frequência: Se olharmos atentamente para os três sinais, notaremos que a frequência dos três sinais é diferente.
se durante o mesmo período de tempo, no sinal 1 há n número de ondas então há 2n número de ondas no sinal 2 e vice-versa.
Fase: Também, quando olhamos de perto para onde o sinal realmente começa. Descobriremos que Enquanto o sinal 1 começa em (0,0), o sinal 2 começa em (-0,5,0) se traçarmos a onda para encontrar o eixo y a 0. Assim, a 0 já temos a amplitude máxima do sinal. Isto é o que chamamos deslocamento de fase.
Amplitude: Todos os três sinais têm amplitudes diferentes, o sinal 1 tem uma amplitude de 1 enquanto que o sinal 2 e o sinal 3 têm uma amplitude de 2 e 3 respectivamente.
Isto é tudo captado numa fórmula matemática elegante e super simples. Assim, nos exemplos acima, se o eixo x for denominado x e o eixo y for denominado y. Podemos gerar y em função de t de tal forma que :

p> usando esta fórmula, podemos gerar qualquer tipo de sinal que quisermos e depois podemos fundi-los e brincar com eles. Por exemplo, se fundirmos os sinais 1, 2 e 3. obteremos um sinal como este :

A matemática por detrás da transformação de Fourier
A ideia principal por detrás da transformação de Fourier é que :
Um sinal contínuo no domínio do tempo pode ser representado de forma única e inequívoca por uma série infinita de sinusoides.
O que é que isto significa?
Significa que, se tivermos um sinal e este sinal for gerado por alguma função x(t), então podemos inventar outra função f(t) tal que :

So, Não importa quão forte é o sinal, podemos encontrar uma função como f(t) que é uma soma de uma série infinita de sinusoides que representarão de facto o sinal na perfeição.
Agora, a questão que se coloca agora é, Como encontramos os coeficientes aqui na equação acima porque estes são os valores que determinariam a forma da saída e, portanto, do sinal.
So, para obter estes coeficientes utilizamos transformadas de Fourier e o resultado da transformação de Fourier é um grupo de coeficientes. Assim, usamos X(F) para denotar os coeficientes de Fourier e é uma função da frequência que obtemos ao resolver o integral de tal forma que :
A parte complicada neste integral é na realidade o i que denota um número complexo. Portanto, provavelmente lembramo-nos que i² = -1 ou i = √-1. Também pode ajudar a lembrar que a forma de um número complexo é a + ib . Assim, tem uma parte real e imaginária.
Também, quando realmente resolvemos o integral acima, obtemos estes números complexos onde a e b correspondem aos coeficientes que procuramos.
Temos contudo três problemas com os quais temos de lidar :
- Como lidar com
i. - Como lidar com sinais discretos.
Então, vamos começar com o segundo.
Para compreender a Transformada Discreta de Fourier, precisamos primeiro de compreender como se pode amostrar um sinal contínuo?
De acordo com a Wikipedia, No processamento de sinais, a amostragem é a redução de um sinal de tempo contínuo para um sinal de tempo discreto. Eis um exemplo de como a forma do sinal muda com a alteração da taxa de amostragem :
Deixe o sinal original ser um sinal com uma amplitude de dois e frequência de cinco ao longo de um período de um segundo :
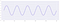
Now, à medida que diminuímos a taxa de amostragem, vejamos como a forma do sinal muda :
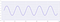
Asso que diminuímos ainda mais a taxa de amostragem, obtemos :

Agora, que sabemos como amostrar os sinais, vamos olhar para a modificação dos algoritmos conhecidos como Transformada Discreta de Fourier.
Transformação de Fourier Discreta
Ainda amostra de sinal de comprimento N no domínio do tempo pode ser representada única e inequivocamente por uma série finita de sinusoides.
Assim, já não temos de lidar com o infinito na nossa nova definição.
Qual é a diferença?
Na Transformada padrão de Fourier, utilizámos uma função de tempo x(t) para gerar um sinal contínuo. Agora, no caso discreto, não temos uma função, temos um conjunto de dados, um conjunto de pontos que obtemos através da amostragem do sinal contínuo. Assim, vou usar {x} para doar um conjunto de dados tal que contenha a leitura da amostragem de tal forma que :
e o que Discreto Fourier Transformará para nós o conjunto de dados de {x} em outro conjunto de dados {X} que conterá os coeficientes de Fourier tais que :
se olharmos para a definição de transformação de Fourier, cada X em {X} é um número complexo e contém o a e b componentes para as frequências.
mas, como é que os dois conjuntos de dados {x} e {X} têm o mesmo comprimento?
se pensarmos, o que impulsiona o comprimento de {x} conjunto de dados é a taxa de amostragem porque, durante um período de tempo, o número de pontos de dados que eu li é exactamente a taxa de amostragem correcta? Se pensarmos no outro conjunto de dados {X} , dizemos que a frequência é o número de ocorrências por unidade de tempo. Portanto, se estou a fazer amostragem com uma certa frequência, não consigo reconhecer sinais que têm uma frequência maior do que a frequência de amostragem só porque não obtemos pontos de dados suficientes.
Então, se tivermos sinais com frequências muito altas numa taxa de amostragem muito baixa, não seremos capazes de reconhecer estes sinais de todo. Assim, o número de frequências que podemos reconhecer aplicando a Transformada de Fourier é, na realidade, impulsionado também pela taxa de amostragem.
Assim, agora que temos o nosso conjunto de dados {x} vamos obter {Xk} tal que é um elemento em {X} que são os meus coeficientes de Fourier tais que :
So, esta é essencialmente a Transformada Discreta de Fourier. Podemos fazer este cálculo e ele produzirá um número complexo na forma de a + ib onde temos dois coeficientes para a série de Fourier.
Agora, sabemos como amostrar sinais e como aplicar uma Transformada de Fourier Discreta. A última coisa que gostaríamos de fazer é, gostaríamos de nos livrar do número complexo i porque não é suportado em mllib ou systemML usando algo conhecido como a fórmula de Euler que afirma :
So, Se ligarmos a fórmula de Euler na equação da Transformada de Fourier, obtemos

também sabemos que cos(-θ) = cos(θ) e sin(-θ) = -sin(θ) e se usarmos isto na equação acima, a equação poderia ser simplificada como :

e podemos de facto quebrar a equação acima em duas somas, de tal forma que :

Now, Se compararmos a equação acima com a equação de um número complexo que é a + ib então obtemos o valor correspondente como :
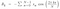
So, agora podemos colocar estes valores na equação de f(t) e obter o resultado.
Conclusion
Na prática utilizamos uma ligeira modificação da Transformada Discreta de Fourier conhecida como Transformada Rápida de Fourier porque a Transformada Discreta de Fourier é muito simples, básica e também lenta. Não é adequada ao fim a que se destina se quisermos realmente fazer algo no ambiente de produção. A complexidade de cálculo da Transformada Discreta de Fourier é tempo quadrático O(n²) e a Transformada Rápida de Fourier para comparação é tempo quase linear O(nlogn). A Transformada Rápida de Fourier faz isto através da exploração da assimetria na Transformada de Fourier.