Objectivos de aprendizagem
No final desta secção, será capaz de:
- descrever a acção de um condensador e definir a capacitância.
- Explicar condensadores de placas paralelas e as suas capacitâncias.
- Discutir o processo de aumentar a capacidade de um dieléctrico.
- Determinar a capacidade dada carga e tensão.
Um condensador é um dispositivo utilizado para armazenar carga eléctrica. Os condensadores têm aplicações que vão desde a filtragem estática da recepção de rádio até ao armazenamento de energia em desfibrilhadores cardíacos. Tipicamente, os condensadores comerciais têm duas partes condutoras próximas uma da outra, mas não tocantes, tais como as da Figura 1. (Na maioria das vezes é utilizado um isolador entre as duas placas para proporcionar separação – ver a discussão sobre dieléctricos abaixo). Quando os terminais das baterias são ligados a um condensador inicialmente não carregado, quantidades iguais de carga positiva e negativa, +Q e -Q, são separadas nas suas duas placas. O condensador permanece globalmente neutro, mas referimo-nos a ele como armazenando uma carga Q nesta circunstância.

Figure 1. Ambos os condensadores aqui mostrados foram inicialmente descarregados antes de serem ligados a uma bateria. Agora têm cargas separadas de +Q e -Q nas suas duas metades. (a) Um condensador de placa paralela. (b) Um condensador enrolado com um material isolante entre as suas duas placas condutoras.
Capacitor
Um condensador é um dispositivo utilizado para armazenar carga eléctrica.
A quantidade de carga Q que um condensador pode armazenar depende de dois factores principais – a tensão aplicada e as características físicas do condensador, tais como o seu tamanho.
A quantidade de carga Q um condensador pode armazenar
A quantidade de carga Q um condensador pode armazenar depende de dois factores principais – a voltagem aplicada e as características físicas do condensador, tais como o seu tamanho.

Figure 2. As linhas de campo eléctrico neste condensador de placa paralela, como sempre, começam em cargas positivas e terminam em cargas negativas. Como a intensidade do campo eléctrico é proporcional à densidade das linhas de campo, é também proporcional à quantidade de carga no condensador.
Um sistema composto por duas placas condutoras paralelas idênticas, separadas por uma distância, como na Figura 2, é chamado condensador de placa paralela. É fácil ver a relação entre a tensão e a carga armazenada para um condensador de placa paralela, como mostra a Figura 2. Cada linha de campo eléctrico começa numa carga positiva individual e termina numa negativa, para que haja mais linhas de campo se houver mais carga. (O desenho de uma única linha de campo por carga é apenas uma conveniência. Podemos desenhar muitas linhas de campo para cada carga, mas o número total é proporcional ao número de cargas). A força do campo eléctrico é, portanto, directamente proporcional a Q.
O campo é proporcional à carga:
E∝Q,
onde o símbolo ∝ significa “proporcional a”. Da discussão em Potencial eléctrico num campo eléctrico uniforme, sabemos que a voltagem através de placas paralelas é
V = Ed.
Thus, V∝E. Segue-se, então, que V∝Q, e inversamente,
Q∝V.
Isto é verdade em geral: Quanto maior for a tensão aplicada a qualquer condensador, maior será a carga nele armazenada.
Diferentes condensadores armazenarão diferentes quantidades de carga para a mesma tensão aplicada, dependendo das suas características físicas. Definimos a sua capacidade C para ser tal que a carga Q armazenada num condensador seja proporcional à C. A carga armazenada num condensador é dada por
Q = CV.
Esta equação expressa os dois principais factores que afectam a quantidade de carga armazenada. Esses factores são as características físicas do condensador, C, e a voltagem, V. Reorganizando a equação, vemos que a capacidade C é a quantidade de carga armazenada por volt, ou
C=frac{Q}{V}{V}.
Capacitância
Capacitância C é a quantidade de carga armazenada por volt, ou
C=\frac{Q}{V}\\
A unidade de capacitância é o farad (F), nomeado por Michael Faraday (1791-1867), um cientista inglês que contribuiu para os campos do electromagnetismo e da electroquímica. Uma vez que a capacitância é carga por unidade de tensão, vemos que um farad é uma coulomb por volt, ou
1\text{ F}=frac{1\text{ C}{1\text{ V}}{1\text{ V}\
Um condensador de 1 coulomb (uma grande quantidade de carga) com a aplicação de apenas 1 volt. Um farad é, portanto, uma capacitância muito grande. Os condensadores típicos variam de fracções de um picofarad (1 pF = 10-12 F) a milifarads (1 mF = 10-3 F).
Figure 3 mostra alguns condensadores comuns. Os condensadores são feitos principalmente de cerâmica, vidro, ou plástico, dependendo da finalidade e tamanho. Os materiais isolantes, chamados dieléctricos, são normalmente utilizados na sua construção, como discutido abaixo.

Figure 3. Alguns condensadores típicos. O tamanho e o valor da capacitância não estão necessariamente relacionados. (crédito: Windell Oskay)
Capacitor de placas paralelas

Figure 4. Condensador de placas paralelas com placas separadas por uma distância d. Cada placa tem uma área A.
O condensador de placas paralelas mostrado na Figura 4 tem duas placas condutoras idênticas, cada uma com uma área de superfície A, separada por uma distância d (sem material entre as placas). Quando uma tensão V é aplicada ao condensador, armazena uma carga Q, como se mostra. Podemos ver como a sua capacitância depende de A e d, considerando as características da força Coulomb. Sabemos que, tal como as cargas repelem, ao contrário das cargas atraem, e a força entre cargas diminui com a distância. Portanto, parece bastante razoável que quanto maiores forem as placas, mais carga podem armazenar – porque as cargas podem espalhar-se mais. Assim, C deveria ser maior para A maior. Da mesma forma, quanto mais próximas estão as placas, maior é a atracção das cargas opostas sobre elas. Assim, C deve ser maior para d.
Pode ser demonstrado que para um condensador de placas paralelas existem apenas dois factores (A e d) que afectam a sua capacidade C. A capacidade de um condensador de placas paralelas em forma de equação é dada por
C=epsilon_{o}frac{A}{d}{d}.
Capacitância de um condensador de placas paralelas
C=\epsilon_{o}frac{A}{d}{d}
A é a área de uma placa em metros quadrados, e d é a distância entre as placas em metros. A constante ε0 é a permissividade do espaço livre; o seu valor numérico em unidades SI é ε0 = 8,85 × 10-12 F/m. As unidades de F/m são equivalentes a C2/N – m2. O pequeno valor numérico de ε0 está relacionado com a grande dimensão do farad. Um condensador de placa paralela deve ter uma grande área para ter uma capacitância aproximando-se de um farad. (Note-se que a equação acima é válida quando as placas paralelas estão separadas por ar ou espaço livre. Quando outro material é colocado entre as placas, a equação é modificada, como discutido abaixo.)
Exemplo 1. Capacitância e carga armazenada num condensador de placas paralelas
- Qual é a capacidade de um condensador de placas paralelas com placas metálicas, cada uma de 1,00 m2 de área, separadas por 1,00 mm?
- Que carga é armazenada neste condensador se lhe for aplicada uma voltagem de 3,00 × 103 V?
Estratégia
Deve encontrar a capacitância C é uma aplicação directa da equação C=epsilon_{o}frac{a}{d}{d Uma vez encontrada C, a carga armazenada pode ser encontrada utilizando a equação Q = CV.
Solução para a Parte 1
Entrar os valores dados na equação para a capacitância de um condensador de placa paralela
\begin{array}{lll}C&&\epsilon_{o}\frac{A}{d}=\left(8.85\times10^{-12}\frac{\text{F}}{\text{m}}\right)\frac{1.00\text{ m}^2}{1.00\times10^{-3}\text{ m}}\\\text{ }&&8.85\times10^{-9}\text{ F}=8.85\text{ nF}{ nF}}end{array}}
Discussão para a Parte 1
Este pequeno valor para a capacitância indica como é difícil fazer um dispositivo com uma grande capacitância. Técnicas especiais ajudam, como a utilização de folhas finas de área muito grande colocadas juntas.
Solução para a Parte 2
A carga armazenada em qualquer condensador é dada pela equação Q = CV. A introdução dos valores conhecidos nesta equação dá
\begin{array}{lll}Q&&CV=esquerda(8.85\ vezes10^{-9}{{F}{direita)|esquerda(3.00\vezes10^{3}text{ V}direita){\i}text{\i1}&
=&26,6mu{C}end{arranjo}
Discussão para a Parte 2
Esta carga é apenas ligeiramente maior do que as encontradas na electricidade estática típica. Uma vez que o ar se decompõe a cerca de 3,00 × 106 V/m, não é possível armazenar mais carga neste condensador aumentando a voltagem.
Outro exemplo biológico interessante que trata do potencial eléctrico é encontrado na membrana de plasma da célula. A membrana expulsa uma célula do seu ambiente e também permite que os iões passem selectivamente para dentro e para fora da célula. Existe uma diferença potencial através da membrana de cerca de -70 mV . Isto deve-se aos iões carregados principalmente negativamente na célula e à predominância de iões de sódio (Na+) carregados positivamente no exterior. As coisas mudam quando uma célula nervosa é estimulada. Os iões Na+ são autorizados a passar através da membrana para dentro da célula, produzindo um potencial positivo de membrana – o sinal nervoso. A membrana da célula tem uma espessura de cerca de 7 a 10 nm. Um valor aproximado do campo eléctrico através dele é dado por
\displaystyle{E}=frac{V}{d}=frac{-70\times10^{-3}}text{ V}}{8\times10^{-9}text{ m}=-9\times10^{6}text{ V/m}
Este campo eléctrico é suficiente para causar uma avaria no ar.
Dielectric
O exemplo anterior realça a dificuldade de armazenar uma grande quantidade de carga em condensadores. Se d for feito menor para produzir uma maior capacidade, então a tensão máxima deve ser reduzida proporcionalmente para evitar avarias (uma vez que E=frac{V}{d}}). Uma solução importante para esta dificuldade é colocar um material isolante, chamado dieléctrico, entre as placas de um condensador e permitir que d seja tão pequeno quanto possível. Não só o d menor torna a capacitância maior, como muitos isoladores podem suportar maiores campos eléctricos do que o ar antes de se avariarem.
Há outro benefício na utilização de um dieléctrico num condensador. Dependendo do material utilizado, a capacitância é maior do que a dada pela equação C=\kappa\epsilon_{0}frac{A}{d}{d}} por um factor κ, chamado constante dieléctrica. Um condensador de placas paralelas com um dieléctrico entre as suas placas tem uma capacitância dada por C=\kappa\epsilon_{0}frac{A}{d}{d}{capacitor de placas paralelas com dieléctrico).
Valores da constante dieléctrica κ para vários materiais são dados na Tabela 1. Note-se que κ para o vácuo é exactamente 1, pelo que a equação acima é válida também nesse caso. Se for utilizado um dieléctrico, talvez colocando Teflon entre as placas do condensador no Exemplo 1, então a capacitância é maior pelo factor κ, que para o Teflon é 2.1.
Take-Home Experiment: Construir um condensador
Quão grande pode ser feito um condensador usando um invólucro de pastilha elástica? As placas serão a folha de alumínio, e a separação (dieléctrica) no meio será o papel.
| Constancia dieléctrica κ | Força dieléctrica (V/m) | |
|---|---|---|
| Vácuo | 1.00000 | – |
| Air | 1.00059 | 3 × 106 |
| 4.9 | 24 × 106 | |
| 3.78 | ||
| 6.7 | 12 × 106 | |
| Nylon | 3.4 | 14 × 106 |
| Papel | 3.7 | 16 × 106 |
| Poliestireno | 2.56 | 24 × 106 |
| Vidro pirex | 5.6 | 14 × 106 |
| Óleo de silício | 2.5 | 15 × 106 |
| Strontium titanate | 233 | 8 × 106 |
| Teflon | 2.1 | 60 × 106 |
| Water | 80 |
Nota também que a constante dieléctrica para o ar está muito próxima de 1, para que os condensadores cheios de ar actuem muito como aqueles com vácuo entre as suas placas, excepto que o ar pode tornar-se condutor se a força do campo eléctrico se tornar demasiado grande. (Relembrar que E=\frac{V}{d}} para um condensador de placas paralelas.) Também mostrado na Tabela 1 são forças máximas de campo eléctrico em V/m, chamadas forças dieléctricas, para vários materiais. Estes são os campos acima dos quais o material começa a decompor-se e a conduzir. A resistência dieléctrica impõe um limite à tensão que pode ser aplicada para uma determinada separação da placa. Por exemplo, no Exemplo 1, a separação é 1.00 mm, e assim o limite de tensão para o ar é
\begin{array}{lll}V&&E\cdot{d}\\\text{ }&&\left(3\times10^6\text{ V/m}\right)\left(1.00\vezes10^{-3}text{ m}direita){\i}text{\i1}&=&3000{\i}text{ V}end{array}
p>No entanto, o limite para uma separação de 1,00 mm cheia de teflon é de 60.000 V, uma vez que a resistência dieléctrica do teflon é de 60 × 106 V/m. Assim, o mesmo condensador cheio com teflon tem uma maior capacidade e pode ser submetido a uma tensão muito maior. Usando a capacitância calculada no exemplo acima para o condensador de placa paralela cheio de ar, descobrimos que o Teflon…condensador cheio pode armazenar uma carga máxima de
\begin{array}{lll}Q&&CV=texto }&&\kappa{C}_{{\i1}{\i1}{\i1}v&=&\i>(2.1)(8.85\text{ nF})(6.0\text 10^4\text{ V}){\text{ }&&1.1\text{ mC}}end{arranjo{\i}
p>Esta é 42 vezes a carga do mesmo condensador cheio de ar.
Resistência dieléctrica
A resistência máxima do campo eléctrico acima da qual um material isolante começa a decompor-se e a conduzir chama-se resistência dieléctrica.
Microscopicamente, como é que um dieléctrico aumenta a capacidade? A polarização do isolador é responsável. Quanto mais facilmente for polarizado, maior é a sua constante dieléctrica κ. A água, por exemplo, é uma molécula polar porque uma extremidade da molécula tem uma ligeira carga positiva e a outra extremidade tem uma ligeira carga negativa. A polaridade da água faz com que esta tenha uma constante dieléctrica relativamente grande de 80. O efeito da polarização pode ser melhor explicado em termos das características da força Coulomb. A figura 5 mostra a separação esquemática da carga nas moléculas de um material dieléctrico colocadas entre as placas carregadas de um condensador. A força Coulomb entre as extremidades mais próximas das moléculas e a carga nas placas é atractiva e muito forte, uma vez que elas estão muito próximas umas das outras. Isto atrai mais carga sobre as placas do que se o espaço estivesse vazio e as cargas opostas estivessem a uma distância d longe.

Figure 5. (a) As moléculas no material isolante entre as placas de um condensador são polarizadas pelas placas carregadas. Isto produz uma camada de carga oposta na superfície do dieléctrico que atrai mais carga para a placa, aumentando a sua capacitância. (b) O dieléctrico reduz a intensidade do campo eléctrico no interior do condensador, resultando numa menor tensão entre as placas para a mesma carga. O condensador armazena a mesma carga para uma tensão menor, implicando que tem uma maior capacitância devido ao dieléctrico.
Outra forma de compreender como um dieléctrico aumenta a capacitância é considerar o seu efeito sobre o campo eléctrico no interior do condensador. A figura 5(b) mostra as linhas do campo eléctrico com um dieléctrico no lugar. Uma vez que as linhas de campo terminam em cargas no dieléctrico, há menos linhas a passar de um lado do condensador para o outro. Assim, a intensidade do campo eléctrico é menor do que se houvesse um vácuo entre as placas, mesmo que a mesma carga esteja sobre as placas. A voltagem entre as placas é V = Ed, pelo que também é reduzida pelo dieléctrico. Assim, existe uma tensão V menor para a mesma carga Q; uma vez que C=\frac{Q}{V}, a capacidade C é maior.
A constante dieléctrica é geralmente definida como \kappa=\frac{E_0}{E_0}, ou a relação do campo eléctrico no vácuo com o do material dieléctrico, e está intimamente relacionada com a polarizabilidade do material.
Coisas Grandes e Pequenas: A Origem Submicroscópica da Polarização
Polarização é uma separação de carga dentro de um átomo ou molécula. Como já foi observado, o modelo planetário do átomo apresenta-o como tendo um núcleo positivo orbitado por electrões negativos, análogo aos planetas que orbitam o Sol. Embora este modelo não seja completamente exacto, é muito útil para explicar uma vasta gama de fenómenos e será aperfeiçoado noutros locais, tais como na Física Atómica. A origem submicroscópica da polarização pode ser modelada como mostrado na Figura 6.

Figure 6. A concepção do artista de um átomo polarizado. As órbitas dos electrões em redor do núcleo são ligeiramente deslocadas pelas cargas externas (mostradas exageradas). A separação resultante da carga dentro do átomo significa que ele é polarizado. Note-se que a carga diferente está agora mais próxima das cargas externas, causando a polarização.
Encontraremos na Física Atómica que as órbitas dos electrões são mais propriamente vistas como nuvens de electrões com a densidade da nuvem relacionada com a probabilidade de encontrar um electrão nesse local (por oposição aos locais e caminhos definidos dos planetas nas suas órbitas em torno do Sol). Esta nuvem é deslocada pela força Coulomb para que o átomo tenha, em média, uma separação de carga. Embora o átomo permaneça neutro, pode agora ser a fonte de uma força Coulomb, uma vez que uma carga trazida para perto do átomo estará mais próxima de um tipo de carga do que a outra.
p>algumas moléculas, tais como as da água, têm uma separação inerente de carga e são assim chamadas moléculas polares. A figura 7 ilustra a separação da carga numa molécula de água, que tem dois átomos de hidrogénio e um átomo de oxigénio (H2O). A molécula da água não é simétrica – os átomos de hidrogénio são repelidos para um lado, dando à molécula uma forma de bumerangue. Os electrões numa molécula de água são mais concentrados em torno do núcleo de oxigénio mais carregado do que em torno dos núcleos de hidrogénio. Isto torna a extremidade de oxigénio da molécula ligeiramente negativa e deixa as extremidades de hidrogénio ligeiramente positivas. A separação inerente da carga nas moléculas polares facilita o seu alinhamento com campos e cargas externas. As moléculas polares apresentam, portanto, maiores efeitos de polarização e têm maiores constantes dieléctricas. Aqueles que estudam a química descobrirão que a natureza polar da água tem muitos efeitos. Por exemplo, as moléculas de água reúnem iões muito mais eficazmente porque têm um campo eléctrico e uma separação de carga para atrair cargas de ambos os sinais. Além disso, tal como foi salientado no capítulo anterior, a água polar fornece um escudo ou uma blindagem dos campos eléctricos nas moléculas altamente carregadas de interesse em sistemas biológicos.

Figure 7. Concepção artística de uma molécula de água. Existe uma separação inerente da carga, pelo que a água é uma molécula polar. Os electrões na molécula são atraídos para o núcleo de oxigénio e deixam um excesso de carga positiva perto dos dois núcleos de hidrogénio. (Note-se que o esquema à direita é uma ilustração rudimentar da distribuição de electrões na molécula da água. Não mostra os números reais de prótons e electrões envolvidos na estrutura.)
PhET Explorations: Capacitor Lab
Explorar como funciona um condensador! Alterar o tamanho das placas e adicionar um dieléctrico para ver o efeito na capacitância. Alterar a voltagem e ver as cargas acumuladas nas placas. Observar o campo eléctrico no condensador. Medir a voltagem e o campo eléctrico.
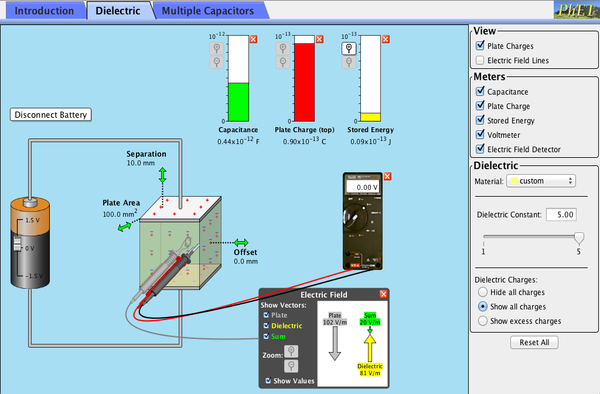
Clique para descarregar a simulação. Executar utilizando Java.
Secção Resumo
- Um condensador é um dispositivo utilizado para armazenar carga.
- A quantidade de carga Q que um condensador pode armazenar depende de dois factores principais – a tensão aplicada e as características físicas do condensador, tais como o seu tamanho.
- A capacitância C é a quantidade de carga armazenada por volt, ou C=\frac{Q}{V}{V}.
- A capacitância de um condensador de placas paralelas é C={\\\\\\\\i}_{0}frac{A}{d}, quando as placas estão separadas por ar ou espaço livre. A capacidade de um condensador de placas paralelas com um dieléctrico entre as suas placas tem uma capacitância dada por C=kappa_epsilon_{0}frac{A}, onde κ é a constante dieléctrica do material.
- A resistência máxima do campo eléctrico acima da qual um material isolante começa a quebrar e a conduzir chama-se resistência dieléctrica.
Perguntas conceptuais
- A capacitância de um dispositivo depende da tensão aplicada? E quanto à carga nele armazenada?
- Utiliza as características da força Coulomb para explicar porque é que a capacitância deve ser proporcional à área da placa de um condensador. Do mesmo modo, explicar porque é que a capacidade deve ser inversamente proporcional à separação entre placas.
- Dê a razão pela qual um material dieléctrico aumenta a capacidade em relação ao que seria com o ar entre as placas de um condensador. Qual é a razão independente pela qual um material dieléctrico também permite que uma maior voltagem seja aplicada a um condensador? (O dieléctrico aumenta assim C e permite uma maior V.)
- Como é que o carácter polar das moléculas de água ajuda a explicar a constante dieléctrica relativamente grande da água? (Ver Figura 7.)
- Espaços ocorrerão entre as placas de um condensador cheio de ar a uma tensão mais baixa quando o ar está húmido do que quando está seco. Explique porquê, considerando o carácter polar das moléculas de água.
- A água tem uma grande constante dieléctrica, mas raramente é utilizada em condensadores. Explique porquê.
- Membranas em células vivas, incluindo as humanas, caracterizam-se por uma separação de carga através da membrana. Efectivamente, as membranas são assim condensadores de carga com funções importantes relacionadas com a diferença potencial através da membrana. É necessária energia para separar estas cargas nas membranas vivas e, se assim for, é a sua fonte a metabolização da energia alimentar ou alguma outra fonte?
/ol>

Figure 8. A membrana semipermeável de uma célula tem diferentes concentrações de iões no interior e no exterior. A difusão move os iões K+ (potássio) e Cl- (cloreto) nas direcções indicadas, até que a força Coulomb interrompa a transferência. Isto resulta numa camada de carga positiva no exterior, uma camada de carga negativa no interior, e portanto uma voltagem através da membrana da célula. A membrana é normalmente impermeável a Na+ (iões de sódio).
Problemas & Exercícios
- Que carga é armazenada num condensador 180 μF quando lhe é aplicada 120 V?
- Li>Cobrir a carga armazenada quando 5.50 V é aplicada a um condensador de 8,00 pF.
- Que carga é armazenada no condensador no Exemplo 1?
- Calcular a tensão aplicada a um condensador de 2,00 μF quando detém 3,10 μC de carga.
- Que tensão deve ser aplicada a um condensador de 8,00 nF para armazenar 0.160 mC de carga?
- Que capacidade é necessária para armazenar 3,00 μC de carga a uma tensão de 120 V?
- Qual é a capacidade de um terminal de um grande gerador Van de Graaff, dado que armazena 8,00 mC de carga a uma tensão de 12,0 MV?
- Qual é a capacidade de um condensador de placas paralelas com placas de área 5,00 m2 que estão separadas por 0,100 mm de Teflon.
- (a)Qual é a capacidade de um condensador de placas paralelas com placas de área 1,50 m2 que estão separadas por 0,0200 mm de borracha de neoprene? (b) Que carga suporta quando lhe é aplicada 9,00 V?
- Conceitos Integrados. Uma partida aplica 450 V a um condensador de 80,0 μF e depois atira-a a uma vítima insuspeita. O dedo da vítima é queimado pela descarga do condensador através de 0,200 g de carne. Qual é o aumento da temperatura da carne? É razoável assumir que não há alteração de fase?
- Resultados irrazoáveis. (a) Um certo condensador de placas paralelas tem placas de área 4,00 m2, separadas por 0,0100 mm de nylon, e armazena 0,170 C de carga. Qual é a voltagem aplicada? (b) O que é que não é razoável sobre este resultado? (c) Que pressupostos são responsáveis ou inconsistentes?
Glossary
capacitor: um dispositivo que armazena carga eléctrica
capacitance: quantidade de carga armazenada por unidade volt
dieléctrica: um material isolante
força dieléctrica: o campo eléctrico máximo acima do qual um material isolante começa a quebrar e a conduzir
condensador de placa paralela: duas placas condutoras idênticas separadas por uma distância
molécula polar: uma molécula com separação inerente de carga
Soluções seleccionadas para problemas & Exercícios
1. 21,6 mC
3. 80,0 mC
5. 20,0 kV
7. 667 pF
9. (a) 4,4 μF; (b) 4,0 × 10-5 C
11. (a) 14,2 kV; (b) A tensão é excessivamente grande, mais de 100 vezes a tensão de ruptura do nylon; (c) A carga assumida é excessivamente grande e não pode ser armazenada num condensador com estas dimensões.