Introduction: PID Controller Design

Neste tutorial vamos introduzir uma estrutura compensadora simples, mas versátil, de feedback: o controlador Proporcional-Integral-Derivativo (PID). O controlador PID é amplamente utilizado porque é muito compreensível e porque é bastante eficaz. Uma atracção do controlador PID é que todos os engenheiros compreendem conceptualmente a diferenciação e integração, pelo que podem implementar o sistema de controlo mesmo sem uma profunda compreensão da teoria do controlo. Além disso, ainda que o compensador seja simples, é bastante sofisticado na medida em que capta a história do sistema (através da integração) e antecipa o comportamento futuro do sistema (através da diferenciação). Vamos discutir o efeito de cada um dos parâmetros PID na dinâmica de um sistema de ciclo fechado e vamos demonstrar como utilizar um controlador PID para melhorar o desempenho de um sistema.

comandos MATLAB chave utilizados neste tutorial são: tf , step , pid , feedback , pidtune

PID Overview

Neste tutorial, consideraremos o seguinte sistema unitário-feedback:

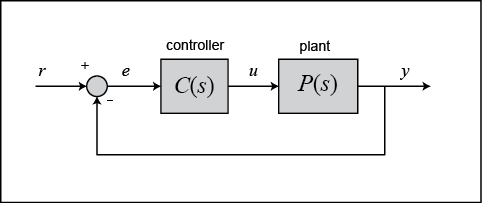
A saída de um controlador PID, que é igual à entrada de controlo para a central, é calculada no domínio do tempo a partir do erro de feedback como se segue:

(1)$ u(t) = K_p e(t) + K_i \int e(t)dt + K_p \frac{de}{dt} $

P>Primeiro, vejamos como funciona o controlador PID num sistema de ciclo fechado usando o esquema mostrado acima. A variável ($e$) representa o erro de seguimento, a diferença entre a saída desejada ($r$) e a saída real ($y$). Este sinal de erro ($e$) é alimentado ao controlador PID, e o controlador calcula tanto a derivada como a integral deste sinal de erro com respeito ao tempo. O sinal de controlo ($u$) para a planta é igual ao ganho proporcional ($K_p$) vezes a magnitude do erro mais a ganho integral ($K_i$) vezes o integral do erro mais o ganho derivado ($K_d$) vezes o derivado do erro.

Este sinal de controlo ($u$) é alimentado à fábrica e a nova saída ($y$) é obtida. A nova saída ($y$) é então alimentada de volta e comparada com a referência para encontrar o novo sinal de erro ($e$). O controlador toma este novo sinal de erro e calcula uma actualização da entrada de controlo. Este processo continua enquanto o controlador estiver em vigor.

A função de transferência de um controlador PID é encontrada tomando a transformação de Laplace da Equação (1).

p>(2)$ K_p + \frac {K_i} {s} + K_d s = \frac{K_d s^2 + K_p s + K_i} {s} $

where $K_p$ = ganho proporcional, $K_i$ = ganho integral, e $K_d$ = ganho derivado.

Podemos definir um controlador PID em MATLAB usando um modelo de função de transferência directamente, por exemplo:

Kp = 1;Ki = 1;Kd = 1;s = tf('s');C = Kp + Ki/s + Kd*s

C = s^2 + s + 1 ----------- s Continuous-time transfer function.

Alternativamente, podemos usar o objecto pid de MATLAB para gerar um controlador de tempo contínuo equivalente, como se segue: 

C = pid(Kp,Ki,Kd)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.

Vamos converter o objecto pid para uma função de transferência para verificar que produz o mesmo resultado que acima:

tf(C)
ans = s^2 + s + 1 ----------- s Continuous-time transfer function.

As Características dos Termos P, I, e D

Aumento do ganho proporcional ($K_p$) tem o efeito de aumentar proporcionalmente o sinal de controlo para o mesmo nível de erro. O facto de o controlador “empurrar” com mais força para um determinado nível de erro tende a fazer com que o sistema de ciclo fechado reaja mais rapidamente, mas também a ultrapassar mais. Outro efeito de aumentar $K_p$ é que tende a reduzir, mas não a eliminar, o erro de estado estável.

A adição de um termo derivado ao controlador ($K_d$) adiciona a capacidade do controlador para “antecipar” o erro. Com controlo proporcional simples, se $K_p$ for fixo, a única forma de o controlo aumentar é se o erro aumentar. Com controlo derivado, o sinal de controlo pode tornar-se grande se o erro começar a inclinar-se para cima, mesmo quando a magnitude do erro ainda é relativamente pequena. Esta antecipação tende a acrescentar amortecimento ao sistema, diminuindo assim o excesso. A adição de um termo derivado, contudo, não tem qualquer efeito sobre o erro de estado estável.

A adição de um termo integral ao controlador ($K_i$) tende a ajudar a reduzir o erro de estado estacionário. Se houver um erro persistente e constante, o integrador constrói e constrói, aumentando assim o sinal de controlo e diminuindo o erro. Uma desvantagem do termo integral, contudo, é que pode tornar o sistema mais lento (e oscilatório) uma vez que quando o sinal de erro muda de sinal, pode demorar algum tempo para o integrador “desenrolar”.

Os efeitos gerais de cada parâmetro do controlador ($K_p$$K_d$$K_i$) num sistema de ciclo fechado estão resumidos na tabela abaixo. Nota: estas directrizes são válidas em muitos casos, mas não em todos. Se quiser realmente saber o efeito da afinação dos ganhos individuais, terá de fazer mais análises, ou terá de realizar testes no sistema real.

Kp
Decrease

Decrease
>
Increase

>>

Muito Variação

>>

Decrease
>
Sem alterações

CL RESPOSTA
TEMPO DE RISE
OVERSHOOT
SETTLING TIME
S-S ERRO
Increase
Small Change
Decrease
Ki
Increase
Decrease
Kd
Decrease

Problema de amostra

Suponha que temos uma massa simples…sistema de amortecedor de molas.

A equação governante deste sistema é

(3)$ m\ddot{x} + b{x}dot{x} + kx = F $$

Tomando a transformação de Laplace da equação governante, obtemos

(4)$ ms^{2}X(s) + bsX(s) + kX(s) = F(s) $

A função de transferência entre a força de entrada $F(s)$ e o deslocamento de saída $X(s)$ então torna-se

(5)$ \frac{X(s)}{F(s)} = \frac{1}{ms^2 + bs + k} $

Let

 m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N

Substituindo estes valores na função de transferência acima referida

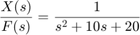
(6)$ \frac{X(s)}{F(s)} = \frac{1}{s^2 + 10s + 20} $

O objectivo deste problema é mostrar como cada um dos termos, $K_p$$K_i$, e $K_d$, contribui para a obtenção dos objectivos comuns de

  • Prazo de subida
  • Espera mínima
  • Zero erro de estado constante

Resposta de passo em aberto

P>Primeira vista da resposta de passo em aberto. Criar um novo ficheiro m e executar o seguinte código: 

s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)

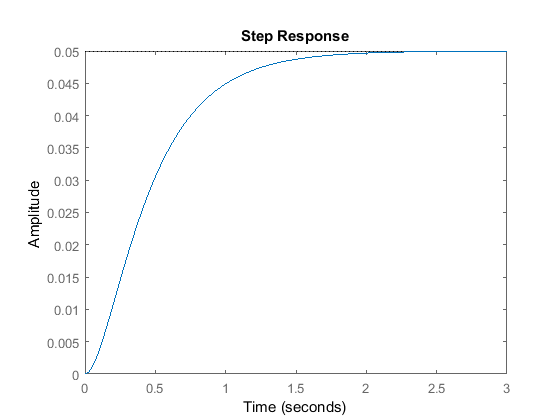
O ganho DC da função de transferência da planta é 1/20, portanto 0,05 é o valor final da saída para uma unidade de passo de entrada. Isto corresponde a um erro de estado estável de 0,95, o que é bastante grande. Além disso, o tempo de subida é de cerca de um segundo, e o tempo de assentamento é de cerca de 1,5 segundos. Vamos conceber um controlador que irá reduzir o tempo de subida, reduzir o tempo de assentamento, e eliminar o erro de estado estacionário.

Controlo proporcional

Da tabela apresentada acima, vemos que o controlador proporcional ($K_p$) reduz o tempo de subida, aumenta o excesso, e reduz o erro de estado estacionário.

A função de transferência em circuito fechado do nosso sistema de feedback de unidades com um controlador proporcional é a seguinte, onde $X(s)$ é a nossa saída (igual a $Y(s)$) e a nossa referência $R(s)$ é a entrada:

(7)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_p}{s^2 + 10s + (20 + K_p)} $

Deixe o ganho proporcional ($K_p$) igual a 300 e mude o m-arquivar para o seguinte: 

Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.

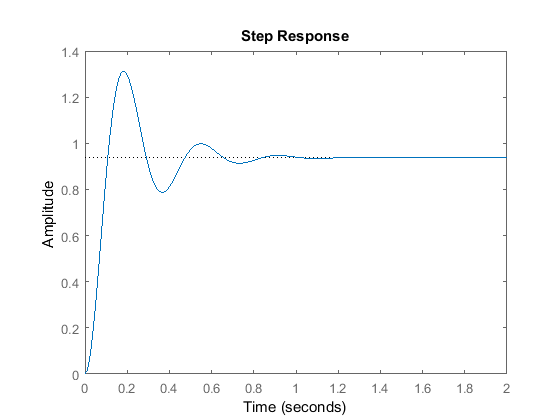
O gráfico acima mostra que o controlador proporcional reduziu tanto o tempo de subida como o erro de estado estacionário, aumentou o excesso, e reduziu o tempo de assentamento numa pequena quantidade.

Controlo Derivado Proporcional

Agora, vamos dar uma olhada no controlo PD. Da tabela acima apresentada, vemos que a adição de controlo de derivados ($K_d$) tende a reduzir tanto o excesso como o tempo de colonização. A função de transferência em circuito fechado do sistema dado com um controlador PD é:

(8)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_d s + K_p}{s^2 + (10 + K_d) s + (20 + K_p)} $

Let $K_p$ igual a 300 como antes e let $K_d$ igual a 10. Introduza os seguintes comandos num ficheiro m e execute-o na janela de comandos MATLAB. 

Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.

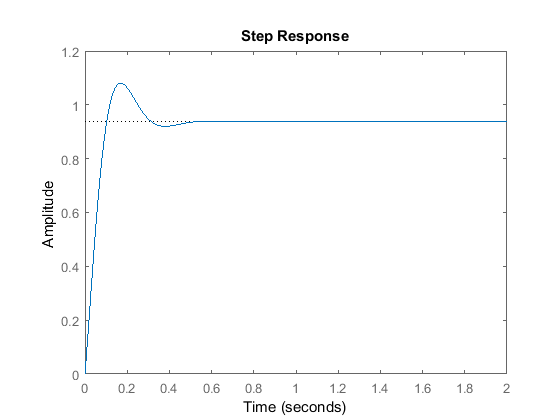
Este gráfico mostra que a adição do termo derivado reduziu tanto o tempo de sobreposição como o de estabilização, e teve um efeito negligenciável sobre o tempo de subida e o erro de estado estacionário.

Controlo proporcional-Integral

Antes de prosseguir para o controlo PID, vamos investigar o controlo PI. Da tabela, vemos que a adição de controlo integral ($K_i$) tende a diminuir o tempo de subida, a aumentar tanto o tempo de sobreposição como o de estabilização, e a reduzir o erro de estado estacionário. Para o sistema dado, a função de transferência em circuito fechado com um controlador PI é:

(9)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_p s + K_i}{s^3 + 10 s^2 + (20 + K_p )s + K_i} $

p>Demos reduzir $K_p$ a 30, e deixe $K_i$ igual a 70. Criar um novo ficheiro m e introduzir os seguintes comandos. 

Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.

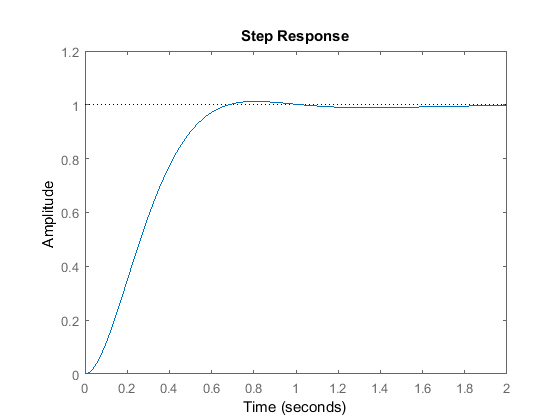
Executar este ficheiro m na janela de comandos MATLAB e deverá gerar o gráfico acima. Reduzimos o ganho proporcional ($K_p$) porque o controlador integral também reduz o tempo de subida e aumenta o excesso como o controlador proporcional faz (efeito duplo). A resposta acima mostra que o controlador integral eliminou o erro de estado estável neste caso.

Controlo proporcional-Integral-Derivativo

Agora, vamos examinar o controlo PID. A função de transferência em circuito fechado do sistema dado com um controlador PID é:

(10)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_d s^2 + K_p s + K_i}{s^3 + (10 + K_d)s^2 + (20 + K_p)s + K_i } $

Depois de várias iterações de afinação, os ganhos $K_p$$K_i$ = 300, e $K_d$ = 50 desde que a resposta desejada. Para confirmar, introduza os seguintes comandos num ficheiro m e execute-o na janela de comandos. Deve obter a seguinte resposta passo. 

Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.

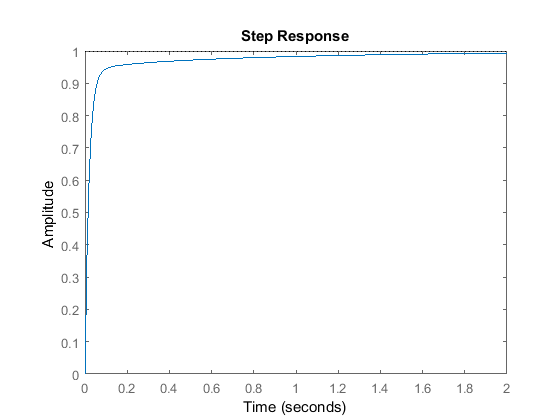
Agora, concebemos um sistema de ciclo fechado sem sobreposição, tempo de subida rápido, e sem erro de estado estável.

Dicas gerais para a concepção de um controlador PID

Quando estiver a conceber um controlador PID para um determinado sistema, siga os passos mostrados abaixo para obter uma resposta desejada.

  1. Obter uma resposta de ciclo aberto e determinar o que precisa de ser melhorado
  2. Adicionar um controlo proporcional para melhorar o tempo de subida
  3. Adicionar um controlo derivado para reduzir o excesso
  4. Adicionar um controlo integral para reduzir o excesso…state error
  5. Ajustar cada um dos ganhos $K_p$$K_i$, e $K_d$ até se obter uma resposta global desejada. Pode sempre consultar a tabela apresentada nesta página “PID Tutorial” para descobrir qual o controlador que controla quais as características.

Por favor, tenha em mente que não precisa de implementar os três controladores (proporcional, derivado, e integral) num único sistema, se não for necessário. Por exemplo, se um controlador PI cumprir os requisitos indicados (como o exemplo acima), então não precisa de implementar um controlador derivado no sistema. Mantenha o controlador tão simples quanto possível.

Um exemplo de afinação de um controlador PI num sistema físico real pode ser encontrado na seguinte ligação. Este exemplo também começa a ilustrar alguns desafios da implementação de controlo, incluindo: saturação de controlo, wind-up integrador, e amplificação de ruído.

Automatic PID Tuning

MATLAB fornece ferramentas para escolher automaticamente os ganhos óptimos do PID, o que torna desnecessário o processo de tentativa e erro descrito acima. Pode aceder ao algoritmo de afinação directamente usando o pidtune ou através de uma agradável interface gráfica de utilizador (GUI) usando o pidTuner.

O algoritmo de afinação automática MATLAB escolhe ganhos PID para equilibrar o desempenho (tempo de resposta, largura de banda) e robustez (margens de estabilidade). Por defeito, o algoritmo desenha para uma margem de fase de 60 graus.

Vamos explorar estas ferramentas automatizadas, gerando primeiro um controlador proporcional para o sistema de amortecimento da mola de massa, introduzindo o comando mostrado abaixo. Na sintaxe mostrada, P é o modelo de planta anteriormente gerado, e ‘p’ especifica que o sintonizador emprega um controlador proporcional. 

 pidTuner(P,'p')

A janela GUI do pidTuner, como a mostrada abaixo, deve aparecer.

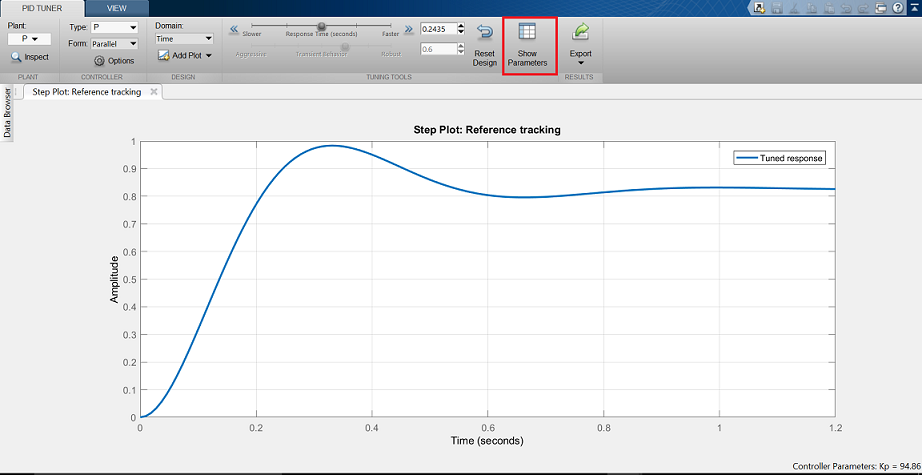
Notificação de que a resposta de passos mostrada é mais lenta do que o controlador proporcional que concebemos à mão. Agora clique no botão Mostrar Parâmetros no canto superior direito. Como esperado, o ganho proporcional, $K_p$, é menor do que o que empregamos, $K_p$< 300.

Agora podemos afinar interactivamente os parâmetros do controlador e ver imediatamente a resposta resultante na janela GUI. Tente arrastar o cursor de Tempo de Resposta para a direita até 0,14 s, como mostra a figura abaixo. Isto faz com que a resposta acelere efectivamente, e podemos ver $K_p$ está agora mais perto do valor escolhido manualmente. Também podemos ver outros parâmetros de desempenho e robustez para o sistema. Note-se que antes de ajustarmos o selector, a margem da fase alvo era de 60 graus. Este é o padrão para o pidTuner e geralmente proporciona um bom equilíbrio entre robustez e desempenho.

Agora vamos tentar conceber um controlador PID para o nosso sistema. Ao especificar o controlador previamente concebido ou (linha de base), C, como segundo parâmetro, pidTuner desenhará outro controlador PID (em vez de P ou PI) e comparará a resposta do sistema com o controlador automatizado com a da linha de base. 

 pidTuner(P,C)

Vemos na janela de saída que o controlador automático responde mais lentamente e exibe mais ultrapassagens do que a linha de base. Agora escolha o Domínio: Opção de frequência a partir da faixa de ferramentas, que revela parâmetros de afinação do domínio de frequência.

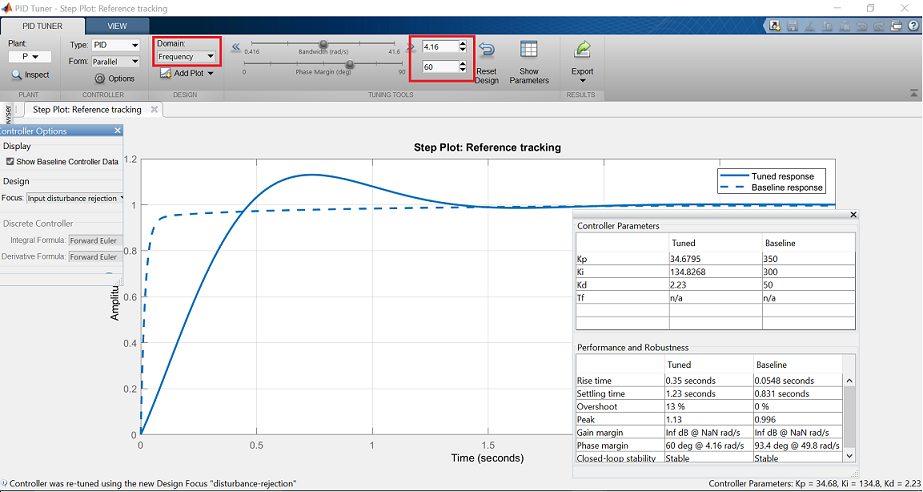
P>Novo tipo em 32 rad/s para largura de banda e 90 graus para margem de fase, para gerar um controlador semelhante em desempenho à linha de base. Tenha em mente que uma maior largura de banda em circuito fechado resulta num tempo de subida mais rápido, e uma maior margem de fase reduz o excesso e melhora a estabilidade do sistema.

Finalmente, notamos que podemos gerar o mesmo controlador utilizando a ferramenta de linha de comando pidtune em vez da GUI pidTuner, empregando a seguinte sintaxe. 

opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90

br>>Publicado com MATLAB® 9.2

Deixe uma resposta

O seu endereço de email não será publicado. Campos obrigatórios marcados com *