Hi there! Esta página web cobre o espaço e o tempo das complexidades Big-O de algoritmos comuns usados na Informática. Ao preparar-me para entrevistas técnicas no passado, dei por mim a passar horas a rastejar pela Internet reunindo as melhores, médias e piores complexidades de algoritmos de pesquisa e classificação para que eu não ficasse perplexo quando me perguntassem sobre eles. Ao longo dos últimos anos, entrevistei em várias empresas de ponta do Vale do Silício, e também algumas empresas maiores, como o Google, Facebook, Yahoo, LinkedIn, e Uber, e cada vez que me preparava para uma entrevista, pensava para mim mesmo “Porque é que alguém não criou uma boa folha de respostas de fraude Big-O?”. Assim, para poupar a todos vocês, gente fina, uma tonelada de tempo, eu fui em frente e criei uma. Aproveitem! – Eric
Veja o El Grapho, uma biblioteca de visualização de dados gráficos que suporta milhões de nós e bordas
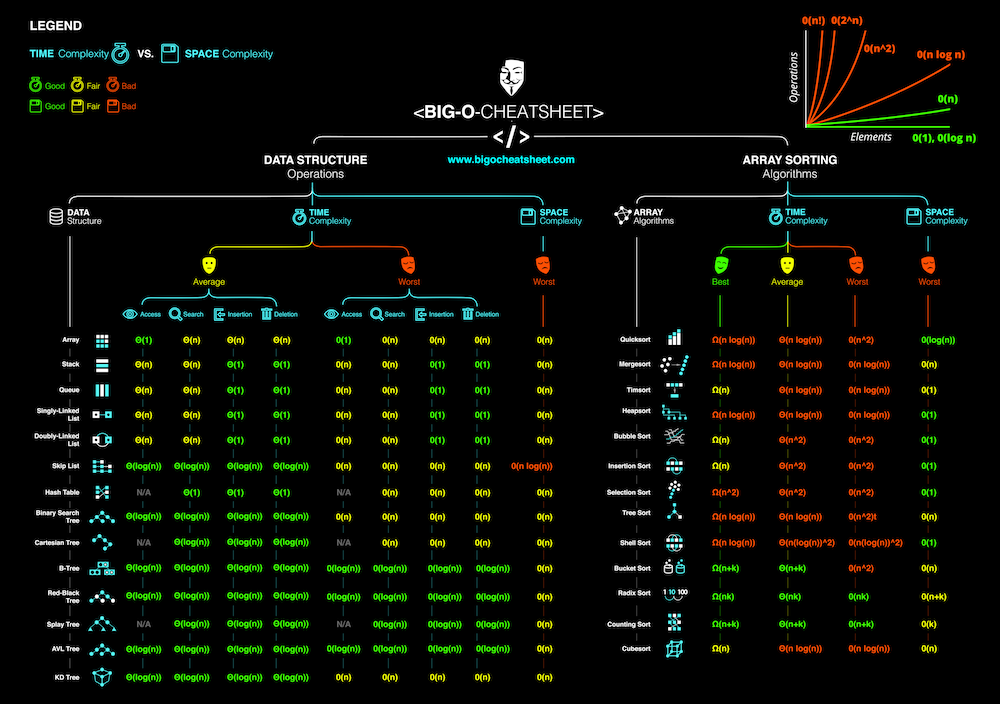
Big-O Gráfico de Complexidade
Horrible |
Bad |
Fair |
Good |
Estrutura Comum de Dados Operações
| Estrutura de Dados | Complexidade Temporal | Complexidade Espacial | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Média | Pior | th>>Worst | th> | Search | Θ(n) |
O(n) |
|||||||
| Stack | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(1) |
|||||||
| Queue | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
||||||||
| Singly-Lista ligada | |||||||||||||
Θ(1) |
O(1) |
||||||||||||
| Skip List | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n log(n)) |
||||||
| Hash Table | N/A |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
||||||||
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
||||||
| Árvore cartesiana | N/A |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(n) |
O(n) |
|||||||
O(log(n)) |
O(log(n)) |
Red-Black Tree | O(log(n)) |
O(log(n)) |
|||||||||
| Splay Tree | N/A |
Θ(log(n)) |
N/A |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
||||||
| AVL Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
|||||
| KD Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
||||
Array Sorting Algorithms
| Algorithm | Time Complexity | Space Complexity | >th>>Best | Average | Worst |
|---|---|---|---|---|
| Quicksort | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
|
| Mergesort | Ω(n log(n)) |
Θ(n log(n)) |
O(n) |
|
| Timsort | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
||
| Bubble Sort | Ω(n) |
Θ(n^2) |
O(1) |
|
| Insertion Sort | Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| Selection Sort | Ω(n^2) |
Θ(n^2) |
||
| Tree Sort | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(n) |
| Shell Sort | Ω(n log(n)) |
Θ(n(log(n))^2) |
O(n(log(n))^2) |
|
Ω(n+k) |
Θ(n+k) |
O(n) |
||
| Radix Sort | Ω(nk) |
O(nk) |
O(n+k) |
|
| Counting Sort | Ω(n+k) |
Θ(n+k) |
||
| Cubesort | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
Aprenda Mais
- Rasgando a Entrevista de Codificação: 150 Perguntas e Soluções de Programação
- Estruturas de Dados e Algoritmos em Java (2ª Edição)
li>Introdução aos Algoritmos, 3ª Edição
JavaScript de Alto Desempenho (Construir Interfaces de Aplicações Web mais Rápidas)
Ganhe a Grande-O Póster da Folha de Cópias
Contribuidores
- Eric Rowell
- Quentin Pleple
- Michael Abed
- Nick Dizazzo
- Adam Forsyth
- Felix Zhu
- Jay Engineer
- Josh Davis
- Nodir Turakulov
- Jennifer Hamon
- David Dorfman
- Bart Massey
- Ray Pereda
- Si Pham
- Mike Davis
- mcverry
- Max Hoffmann
- Alejandro Ramirez
- Clay Tyler
- Orhan Can Ozalp
- Ayman Singh
- David Morton
- Aurelien Ooms
- Sebastian Paaske Torholm
- Koushik Krishnan
- Drew Bailey
- Robert Burke
li>Bahador Saketli>Damon Davisonli>Alvin Wanli>Alan Briolatli>Drew Hannayli>Andrew Rasmussenli>Dennis Tsangli>Vinnie Magroli>Adam Arold
li>Aneel Nazarethli>Rahul Chowdhuryli>Jonathan McElroyli>steven41292li>Brandon Amosli>Joel Friedlyli>Casper Van Gheluweli>Eric Lefevre-.Ardantli>Olegli>Renfred Harperli>Piper Chesterli>Miguel Amigotli>Apurva Kli>Matthew Daroncoli>Yun-Cheng Lin
Faça esta Página Melhor
Edite estas tabelas!