Como lidar com Eventos Dependentes
A vida está cheia de eventos aleatórios! É preciso obter uma “sensação” para eles serem uma pessoa inteligente e bem sucedida.
Eventos independentes
Os eventos podem ser “Independentes”, significando que cada evento não é afectado por quaisquer outros eventos.
Exemplo: Atirar uma moeda ao ar.
Cada atirada de uma moeda é uma coisa isolada perfeita.
O que fez no passado não afectará o actual arremesso.
A hipótese é simplesmente 1 em 2, ou 50%, tal como QUALQUER arremesso da moeda.
Assim, cada arremesso é um Evento Independente.
Eventos dependentes
Mas os eventos também podem ser “dependentes” … o que significa que podem ser afectados por eventos anteriores …
Exemplo: Mármores num saco
2 mármores azuis e 3 vermelhos estão num saco.
Quais são as probabilidades de obter um mármore azul?
A probabilidade é de 2 em 5
Mas depois de tirar um, as probabilidades mudam!
Assim, da próxima vez:
br> se antes tivéssemos um mármore vermelho, então a hipótese de um mármore azul a seguir é 2 em 4
br> se antes tivéssemos um mármore azul, então a hipótese de um mármore azul a seguir é 1 em 4
Isto é porque estamos a remover os mármores do saco.
Então o próximo evento depende do que aconteceu no evento anterior, e é chamado dependente.
Substituição
Nota: se substituirmos os berlindes no saco de cada vez, então as hipóteses não mudam e os eventos são independentes:
- Com Substituição: os eventos são Independentes (as probabilidades não mudam)
- Sem Substituição: os eventos são Dependentes (as probabilidades mudam)
Eventos Dependentes são o que vemos aqui.
Diagrama da Árvore
Um Diagrama da Árvore:é uma forma maravilhosa de imaginar o que se está a passar, por isso vamos construir um para o nosso exemplo dos mármores.
Existe uma hipótese de 2/5 de arrancar um mármore Azul, e uma hipótese de 3/5 para o Vermelho:
p> Podemos ir um passo mais longe e ver o que acontece quando escolhemos um segundo mármore:
Se um mármore azul foi seleccionado primeiro, há agora uma probabilidade de 1/4 de obter um mármore azul e uma probabilidade de 3/4 de obter um mármore vermelho.
Se um mármore vermelho foi seleccionado primeiro, há agora uma probabilidade de 2/4 de obter um mármore azul e uma probabilidade de 2/4 de obter um mármore vermelho.
Agora podemos responder a perguntas como “Quais são as hipóteses de desenhar 2 mármores azuis?”
Resposta: é uma hipótese 2/5 seguida de uma hipótese 1/4:
P>Viu como multiplicámos as hipóteses? E obtivemos 1/10 como resultado.
As hipóteses de desenhar 2 mármores azuis é 1/10
Notação
Adoramos a notação em matemática! Isto significa que podemos então usar o poder da álgebra para brincar com as ideias. Portanto, aqui está a notação para probabilidade:
P(A) significa “Probabilidade do Evento A”
No nosso exemplo de mármore, o Evento A é “get a Blue Marble first” com uma probabilidade de 2/5:
P(A) = 2/5
E o Evento B é “get a Blue Marble second” … mas para isso temos 2 escolhas:
- Se primeiro obtivermos um Mármore Azul a probabilidade é agora 1/4
- Se primeiro obtivermos um Mármore Vermelho a probabilidade é agora 2/4
Por isso temos de dizer qual deles queremos, e usar o símbolo “|” para significar “dado”:
P(B|A) significa “Evento B dado Evento A”
Por outras palavras, o evento A já aconteceu, agora qual é a hipótese do evento B?
P(B|A) também é chamado “Probabilidade Condicional” de B dado A.
E no nosso caso:
P(B|A) = 1/4
Por isso, a probabilidade de obter 2 berlindes azuis é:
E escrevemos como
“Probabilidade do evento A e evento B é igual a
a probabilidade do evento A vezes a probabilidade do evento B dado evento A”
Vamos fazer o próximo exemplo usando apenas a notação:
Exemplo: Desenhar 2 Reis de um Convés
Evento A está a desenhar um Rei primeiro, e o Evento B está a desenhar um Rei segundo.
Para a primeira carta a probabilidade de desenhar um Rei é de 4 de 52 (há 4 Reis num baralho de 52 cartas):
P(A) = 4/52
Mas depois de retirar um Rei do baralho a probabilidade da segunda carta desenhada é menor (apenas 3 das 51 cartas restantes são Reis):
P(B|A) = 3/51
E assim:
P(A e B) = P(A) x P(B|A) =(4/52)x (3/51) = 12/2652 = 1/221
Assim, a probabilidade de obter 2 Reis é de 1 em 221, ou cerca de 0.5%
Encontrar dados ocultos
Usando Álgebra podemos também “mudar o assunto” da fórmula, assim:
| Iniciar com: | P(A e B) = P(A) x P(B|A) | |
| Swap sides: | P(A) x P(B|A) = P(A e B) | |
| Divide by P(A): | P(B|A) = P(A e B) / P(A) |
E temos outra fórmula útil:
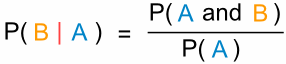
“A probabilidade do evento B dado evento A é igual a
a probabilidade do evento A e do evento B dividida pela probabilidade do evento A
Exemplo: Gelado
70% dos seus amigos gostam de Chocolate, e 35% gostam de Chocolate E gostam de Morango.
Que percentagem dos que gostam de Chocolate também gostam de Morango?
P(Morango|Chocolate) = P(Chocolate e Morango) / P(Chocolate)
50% dos seus amigos que gostam de Chocolate também gostam de Morango
Grande Exemplo: Jogo de futebol
Vocês vão ao futebol, e querem ser o Guarda-redes, mas isso depende de quem é o treinador hoje:
- com o treinador Sam a probabilidade de ser Guarda-redes é 0.5
- com o treinador Alex a probabilidade de ser Guarda-redes é 0.3
Sam é Treinador mais frequentemente … cerca de 6 em cada 10 jogos (uma probabilidade de 0,6).
P>Então, qual é a probabilidade de ser Guarda-redes hoje?
P>Vamos construir um diagrama em árvore. Primeiro mostramos os dois possíveis treinadores: Sam ou Alex:
A probabilidade de obter Sam é 0,6, por isso a probabilidade de Alex deve ser 0,4 (juntos a probabilidade é 1)
Agora, se obtiver Sam, há 0,5 probabilidade de ser Goalie (e 0.5 de não ser Goalie):
se obtiver Alex, há 0,3 probabilidade de ser Goalie (e 0.7 não):
O diagrama de árvore está completo, agora vamos calcular as probabilidades globais. Lembre-se de que:
P(A e B) = P(A) x P(B|A)
P>Aí está como fazê-lo para o ramo “Sam, Yes”:
(Quando tomamos o 0.6 hipóteses de Sam ser treinador vezes a 0,5 hipóteses de Sam lhe deixar ser Goalkeeper acabamos com uma 0,3 hipóteses.)
Mas ainda não terminámos! Ainda não incluímos Alex como Treinador:
Uma 0,4 hipótese de Alex como Treinador, seguido de uma 0,3 hipótese dá 0,12
E os dois ramos “Sim” da árvore juntos fazem:
0,3 + 0,12 = 0.42 probabilidade de ser um Goalkeeper hoje
(É uma probabilidade de 42%)
Check
Um passo final: completar os cálculos e certificar-se de que acrescentam a 1:
0.3 + 0,3 + 0,12 + 0,28 = 1
Sim, eles adicionam a 1, para que pareça correcto.
Amigos e Números Aleatórios
Aqui está outro exemplo bastante diferente de Probabilidade Condicional.
4 amigos (Alex, Blake, Chris e Dusty) escolhem cada um um um número aleatório entre 1 e 5. Qual é a hipótese de qualquer um deles escolher o mesmo número?
p>Soma os nossos amigos um de cada vez …
Primeiro, qual é a hipótese de Alex e Blake terem o mesmo número?
Blake compara o seu número com o número de Alex. Há uma hipótese de 1 em 5 de uma correspondência.
Como um diagrama de árvore:
p>Nota: “Sim” e “Não” juntos faz 1
(1/5 + 4/5 = 5/5 = 1)
Agora, vamos incluir Chris …
Mas agora há dois casos a considerar:
- Se Alex e Blake corresponderam, então Chris tem apenas um número para comparar com.
- Mas se Alex e Blake não corresponderam, então Chris tem dois números para comparar.
E obtemos isto:
eventos dependentes 2
Para a linha superior (Alex e Blake corresponderam) já temos uma correspondência (uma hipótese de 1/5).
Mas para o “Alex e Blake não coincidiram” existe agora uma probabilidade de 2/5 de Chris coincidir (porque Chris consegue igualar o seu número contra ambos Alex e Blake).
E podemos calcular a probabilidade combinada multiplicando as hipóteses de lá chegar:
Seguindo o caminho “Não, Sim” … há uma probabilidade 4/5 de Não, seguida de uma probabilidade 2/5 de Sim:
Seguindo o caminho “Não, Não” …. há uma probabilidade de 4/5 de Não, seguida de 3/5 de Não:
Também notar que quando somamos todas as hipóteses juntas ainda temos 1 (uma boa verificação de que não cometemos um erro):
(5/25) + (8/25) + (12/25) = 25/25 = 1
Agora o que acontece quando incluímos o Dusty?
É a mesma ideia, apenas mais:
OK, isto é, todos os 4 amigos, e as hipóteses de “Sim” juntos fazem 101/125:
Resposta: 101/125
Mas aqui está algo interessante… se seguirmos o caminho do “Não” podemos saltar todos os outros cálculos e tornar a nossa vida mais fácil:
As hipóteses de não corresponder são:
(4/5) × (3/5) × (2/5) = 24/125
Por isso as probabilidades de correspondência são:
1 – (24/125) = 101/125
(E não precisávamos realmente de um diagrama em árvore para isso!)