
/div>
Regressão Logística foi utilizada nas ciências biológicas no início do século XX. Foi então utilizada em muitas aplicações das ciências sociais. A Regressão Logística é utilizada quando a variável dependente (alvo) é categórica.
Por exemplo,
- Para prever se um e-mail é spam (1) ou (0)
- Se o tumor é maligno (1) ou não (0)
Considerar um cenário em que precisamos de classificar se um e-mail é spam ou não. Se utilizarmos a regressão linear para este problema, há necessidade de estabelecer um limiar com base no qual a classificação pode ser feita. Digamos que se a classe real for maligna, valor contínuo previsto 0,4 e o valor limiar é 0,5, o ponto de dados será classificado como não maligno, o que pode levar a consequências graves em tempo real.
Deste exemplo, pode inferir-se que a regressão linear não é adequada para o problema de classificação. A regressão linear não tem limites, e isto traz à luz a regressão logística. O seu valor varia estritamente de 0 a 1.
Regressão logística simples
(Código fonte completo: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Modelo
Eliminar = 0 ou 1
Hipótese => Z = WX + B
hΘ(x) = sigmóide (Z)
Sigmóide Função

Se ‘Z’ for para o infinito, Y(previsto) tornar-se-á 1 e se ‘Z’ for para o infinito negativo, Y(previsto) tornar-se-á 0.
Análise da hipótese
O resultado da hipótese é a probabilidade estimada. Isto é utilizado para inferir quão confiante pode o valor previsto ser o valor real quando se dá um input X. Considere o exemplo abaixo,
X = =
Baseado no valor x1, digamos que obtivemos a probabilidade estimada de ser 0,8. Isto indica que há 80% de probabilidade de um e-mail ser spam.
p> Matematicamente isto pode ser escrito como,

/div>
p> Justifica o nome ‘regressão logística’. Os dados encaixam-se no modelo de regressão linear, que depois são actuados por uma função logística que prevê a variável categórica dependente do alvo.
Tipos de Regressão Logística
1. Regressão Logística Binária
A resposta categórica tem apenas dois resultados possíveis. Exemplo: Spam ou Não
2. Regressão logística multinomial
Três ou mais categorias sem ordenação. Exemplo: Prever quais os alimentos preferidos mais (Veg, Não-Veg, Vegan)
3. Regressão logística ordinal
Três ou mais categorias com ordenação. Exemplo: Classificação do filme de 1 a 5
Limite de decisão
Para prever a que classe pertence um dado, pode ser definido um limite. Com base neste limiar, a probabilidade estimada obtida é classificada em classes.
Diga, se previr_valor ≥ 0,5, então classifique o e-mail como spam, e não como spam.
Limite de decisão pode ser linear ou não-linear. A ordem polinomial pode ser aumentada para obter um limite de decisão complexo.
Função de custo
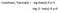
>>div>>>figcaption>Figure 4: Função Custo da Regressão Logística
Porquê a função custo que tem sido usada para linear não pode ser usada para logística?
Regressão linear utiliza erro quadrático médio como função de custo. Se esta for utilizada para regressão logística, então será uma função não convexa de parâmetros (theta). A descida gradual só convergirá para o mínimo global se a função for convexa.

Explicação da função de custo


função de custo simplificada

Porquê esta função de custo?
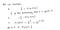
>figcaption>Figure 9: Máxima Verossimilhança Explicação parcial -1
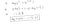
Esta função negativa é porque quando treinamos, precisamos de maximizar a probabilidade minimizando a função de perda. Diminuir o custo aumentará a probabilidade máxima assumindo que as amostras são retiradas de uma distribuição identicamente independente.
Derivando a fórmula para o Algoritmo de Descida Gradiente


Python Implementation
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Custo vs Número_de_Iterações

A precisão do sistema de treino e teste é 100%
Esta implementação é para regressão logística binária. Para dados com mais de 2 classes, a regressão softmax tem de ser utilizada.
Este é um post educacional e inspirado no curso de aprendizagem profunda do Prof. Andrew Ng.
Código completo : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb