Existem diferentes tipos de singularidades, cada uma com características físicas diferentes que têm características relevantes para as teorias das quais emergiram originalmente, tais como as diferentes formas das singularidades, cónicas e curvilíneas. Também foi feita a hipótese de ocorrerem sem Horizontes de Eventos, estruturas que delimitam uma secção de espaço-tempo de outra em que os eventos não podem afectar para além do horizonte; estas são chamadas naked.
ConicalEdit
Uma singularidade cónica ocorre quando existe um ponto em que o limite de cada diffeomorfismo invariante é finito, caso em que o espaço-tempo não é liso no ponto do limite em si. Assim, o espaço-tempo parece um cone em torno deste ponto, onde a singularidade está localizada na ponta do cone. A métrica pode ser finita em todos os lugares onde o sistema de coordenadas é utilizado.
Um exemplo de tal singularidade cónica é uma corda cósmica e um buraco negro Schwarzschild.
CurvatureEdit
Soluções às equações da relatividade geral ou outra teoria da gravidade (como a supergravidade) resultam frequentemente em pontos de encontro onde a métrica explode até ao infinito. Contudo, muitos destes pontos são completamente regulares, e os infinitos são apenas o resultado da utilização de um sistema de coordenadas inadequado neste ponto. A fim de testar se existe uma singularidade num determinado ponto, deve-se verificar se neste ponto as quantidades invariantes de diffeomorfismo (i.e. escalares) se tornam infinitas. Tais quantidades são as mesmas em todos os sistemas de coordenadas, pelo que estes infinitos não “desaparecem” por uma mudança de coordenadas.
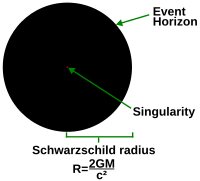
Um exemplo é a solução Schwarzschild que descreve um buraco negro não rotativo e não carregado. Em sistemas de coordenadas convenientes para trabalhar em regiões afastadas do buraco negro, uma parte da métrica torna-se infinita no horizonte do evento. No entanto, o espaço-tempo no horizonte do evento é regular. A regularidade torna-se evidente quando se muda para outro sistema de coordenadas (como as coordenadas Kruskal), onde o sistema métrico é perfeitamente suave. Por outro lado, no centro do buraco negro, onde a métrica também se torna infinita, as soluções sugerem a existência de uma singularidade. A existência da singularidade pode ser verificada observando que o escalar Kretschmann, sendo o quadrado do tensor Riemann i.e. R μ ν ρ σ R μ ν ρ σ R_mu {\displaystyle R_{\mu {\rho {\rho }R^{\mu {\rho {\rho }sigma}

, que é diffeomorphism invariant, é infinito.
Enquanto num buraco negro não rotativo a singularidade ocorre num único ponto nas coordenadas do modelo, chamado “singularidade do ponto”, num buraco negro rotativo, também conhecido como buraco negro de Kerr, a singularidade ocorre num anel (uma linha circular), conhecido como “singularidade do anel”. Tal singularidade pode também teoricamente tornar-se num buraco de verme.
Mais geralmente, um espaço-tempo é considerado singular se estiver geodésicamente incompleto, o que significa que existem partículas em queda livre cujo movimento não pode ser determinado para além de um tempo finito, estando após o ponto de alcançar a singularidade. Por exemplo, qualquer observador dentro do horizonte de eventos de um buraco negro não rotativo cairia no seu centro dentro de um período de tempo finito. A versão clássica do modelo cosmológico do universo do Big Bang contém uma singularidade causal no início do tempo (t=0), onde todas as geodésicas semelhantes ao tempo não têm extensões para o passado. Extrapolando para trás para este hipotético tempo 0 resulta num universo com todas as dimensões espaciais de tamanho zero, densidade infinita, temperatura infinita, e curvatura espaço-tempo infinita.
Singularidade nuaEditar
Até ao início dos anos 90, acreditava-se amplamente que a relatividade geral esconde toda a singularidade por detrás de um horizonte de eventos, tornando as singularidades nuas impossíveis. Isto é referido como a hipótese de censura cósmica. Contudo, em 1991, os físicos Stuart Shapiro e Saul Teukolsky realizaram simulações por computador de um plano rotativo de poeira que indicavam que a relatividade geral poderia permitir singularidades “nuas”. Desconhece-se como seriam realmente estes objectos num tal modelo. Também não se sabe se as singularidades continuariam a surgir se os pressupostos simplificadores utilizados para fazer a simulação fossem removidos. No entanto, é feita a hipótese de que a luz que entra numa singularidade teria igualmente a sua geodésica terminada, fazendo assim com que a singularidade nua parecesse um buraco negro.
Existem horizontes de eventos desaparecidos na métrica Kerr, que é um buraco negro giratório no vácuo, se o momento angular ( J {\displaystyle J}

) for suficientemente alto. Transformando a métrica Kerr em coordenadas Boyer-Lindquist, pode ser mostrado que a coordenada (que não é o raio) do horizonte do evento é, r ± = μ ± ( μ 2 – a 2 ) 1 / 2 {\pm }==mu ^{2}{2}} ^{1/2}}}

, onde μ = G M / c 2 {\i=GM/c^{2}}

, e a = J / M c {\displaystyle a=J/Mc}

. Neste caso, “os horizontes do evento desaparecem” significa quando as soluções são complexas para r ± {\\i1}r_pm {\i}}.

, ou μ 2 < a 2 {\mu ^{2}<a^{2}}

. No entanto, isto corresponde a um caso em que J ^displaystyle J}

excede G M 2 / c {\displaystyle GM^{2}/c}

(ou em unidades Planck, J > M 2 {\displaystyle J>M^{2}}

), ou seja, o spin excede o que é normalmente visto como o limite superior dos seus valores fisicamente possíveis.
Similiarmente, os horizontes de eventos de desaparecimento também podem ser vistos com a geometria Reissner-Nordström de um buraco negro carregado se a carga ( Q {\displaystyle Q}

) for suficientemente alta. Nesta métrica, pode ser demonstrado que as singularidades ocorrem em r ± = μ ± ( μ 2 – q 2 ) 1 / 2 {\i1 {\i1}==mu ^{2}-q^{2})^{1/2}}{1/2}}

, onde μ = G M / c 2 {\displaystyle ^mu =GM/c^{2}}

, e q 2 = G Q 2 / ( 4 π ϵ 0 c 4 ) {\displaystyle q^{2}=GQ^{2}/(4\pi ^epsilon _{0}c^{4})}

. Dos três casos possíveis para os valores relativos de μ {\i} {\i1}displaystyle {\i}

e q {\displaystyle q}

, o caso em que μ 2 < q 2 {\i}<q^{2}}

causa ambos r ± {\i1}displaystyle r_{\i}{\i}

para ser complexo. Isto significa que a métrica é regular para todos os valores positivos de r {\i1}displaystyle r}

, ou por outras palavras, a singularidade não tem horizonte de evento. No entanto, isto corresponde a um caso em que Q / 4 π ϵ 0 {\i}displaystyle Q/{\i}{4\i {\i}epsilon _{0}}}}
 {\i1}displaystyle Q/{\i}{4\i {\i}epsilon _{0}}}}
{\i1}displaystyle Q/{\i}{4\i {\i}epsilon _{0}}}}excede M G {\i}displaystyle M{\i}{\i}
 “>div>>>div> M {\i1c9fbbe”>”8ef1c9fbbbe”>”>div>M”>
“>div>>>div> M {\i1c9fbbe”>”8ef1c9fbbbe”>”>div>M”>
), ou seja, a carga excede o que é normalmente visto como o limite superior dos seus valores fisicamente possíveis. Além disso, não se espera que os buracos negros astrofísicos reais possuam qualquer carga apreciável.
Um buraco negro que possua o menor M {\displaystyle M}

valor consistente com o seu J {\displaystyle J}

e Q {\i1}displaystyle Q

valores e os limites acima referidos, ou seja, um apenas no ponto de perder o seu horizonte de eventos, é denominado de extremo.