Guinguette Marais Poitevin

Sudoku SolverSudoku GeneratorSudoku SolverDaily SudokuKiller Sudoku GeneratorKiller Sudoku SolverSuper Sudoku GeneratorSuper Sudoku SolverSamurai GeneratorSamurai SolverGodoku SolverHomeNewsHow To Play SudokuSign Up!Perfil de MembroCompetiçãoO Programa de SudokuSudoku FAQSudokuNewsletterLivros de SudokuLinksSudokuSudoku SyndicationContacte-nos

Como visto no Times Online em Fevereiro de 2007

Em Novembro de 2006, The Times introduziu um novo nível extremo de Sudoku dando aos jogadores um nível mais difícil de lógica: Super Fiendish. Muitos saudaram o novo desafio, mas alguns pediram ajuda. Assim, à medida que aumentamos a dificuldade Super Fiendish, chegou o momento de apresentar as técnicas essenciais para resolver os puzzles de Sudoku mais difíceis.

Por favor, tenha a certeza de que todos os puzzles de Sudoku publicados no Times são sempre resolvidos por meios lógicos. Aqui apresentamos as técnicas que o ajudarão a resolver os puzzles mais difíceis usando apenas lógica e sem adivinhações.

P>Primeiro alguns pontos preliminares: se alguma vez completou algum Fiendish ou Super Fiendish Sudoku, estará familiarizado em anotar candidatos ou marcas de lápis. As marcas de lápis são pequenos números, geralmente escritos no topo de cada quadrado não resolvido, listando todos os valores possíveis para esse quadrado. Com muitas técnicas avançadas, a chave é identificar padrões dentro das suas marcas de lápis para eliminar possibilidades dentro de outros quadrados. Sempre que resolver um quadrado, deve remover esse número das marcas de lápis em todos os outros quadrados na mesma linha, coluna e bloco.

A técnica da asa x

Essencialmente, este método utiliza o facto de, em certos casos, existirem apenas duas formas possíveis de colocar dois números em quatro quadrados que formam um rectângulo. Existe uma relação entre os quadrados diagonalmente opostos, daí o “x” na asa x. O próprio termo ala x deriva dos combatentes da ala x em Star Wars.

O Sudoku na Fig. 1 é parcialmente resolvido utilizando técnicas de resolução fácil e de dificuldade média: solteiros, solteiros ocultos e intersecções coluna/bloco. Agora, não é possível resolver mais quadrados com estas técnicas; está-se preso. No diagrama há marcas de lápis completas para todos os quadrados nas linhas três e sete, e uma intersecção coluna/bloco necessária para eliminar uma marca de 7 lápis.

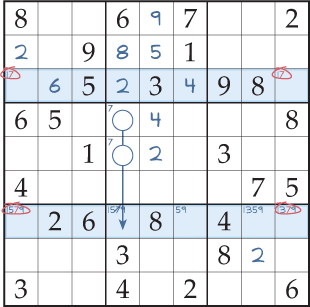Figure 1

Considerando onde pode colocar o 7 na terceira e sétima linhas (destacado). Sabe que deve ser colocado uma vez, e apenas uma vez, em cada uma destas filas. Aqui, os únicos quadrados com o 7 como possibilidade estão na primeira e última colunas. É um facto que não se pode colocar o 7 na primeira coluna quadrada de ambas as linhas em destaque ao mesmo tempo. Também não é possível colocá-los ambos na última coluna. Portanto, devem ser colocados em cantos diagonalmente opostos: um 7 na primeira coluna; um 7 na última.

Então, há duas formas possíveis de colocar o 7; como é que isto o ajuda a resolver alguma coisa? Bem, estabeleceu que os 7 da primeira coluna devem ser colocados numa das duas filas destacadas; não em qualquer outro quadrado desta coluna. Agora pode riscar a marca dos 7 lápis de todos os outros quadrados da primeira coluna. Usando a mesma lógica na última coluna, pode também eliminar o 7 como uma possibilidade de todos os quadrados que não estejam em nenhuma das linhas destacadas (Fig. 2). Isto deixa um quadrado na primeira coluna com apenas uma marca de lápis, pelo que pode agora colocar o 9. Agora este quadrado está resolvido, pode completar o Sudoku usando métodos fáceis.

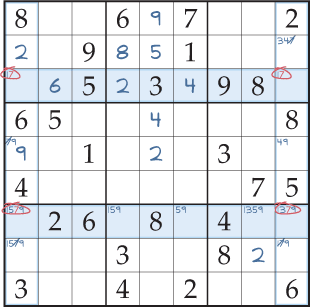Figure 2

Em geral, encontra-se uma asa x quando para duas filas, existem dois, e apenas dois, quadrados possíveis nos quais um determinado número pode ser colocado, e para ambas as filas estes quadrados encontram-se nas mesmas duas colunas. Neste caso, este número particular pode ser eliminado como uma possibilidade para todos os outros quadrados nessas duas colunas. Claro que, nesta definição, é possível trocar linhas e colunas.

A técnica do espadarte

Este é um método mais difícil, um dos mais complicados para qualquer Sudoku que encontrará na impressão. A partir de hoje, a técnica do peixe-espada tornar-se-á uma característica regular no Times2 . O espadarte é semelhante à técnica do asa x, mas numa escala maior, com três filas e colunas em vez de duas. A técnica do espadarte tem o nome de um biplano da Segunda Guerra Mundial chamado “Fairey Swordfish”, um biplano de Reconhecimento de Espadarte de Torpedo utilizado pela Marinha Real de 1936 a 1945. Se forem traçadas linhas ao longo das linhas e colunas, ligando os quadrados envolvidos, estes podem formar dois rectângulos, ligados nos cantos. Isto assemelha-se às asas de um biplano, separadas por escoras.

Encontra-se um espadarte quando para três linhas, há dois ou três quadrados possíveis nos quais um determinado número pode ser colocado, e para as três linhas estes quadrados encontram-se nas mesmas três colunas. Neste caso, este número particular pode ser eliminado como uma possibilidade para todos os outros quadrados nessas três colunas. Naturalmente, é possível trocar linhas e colunas nesta definição.

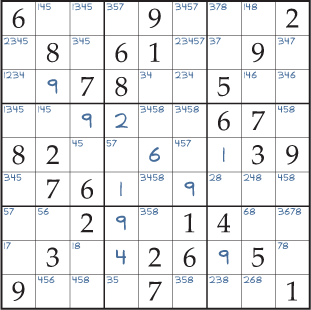Figure 3

Fig. 3 é um Sudoku parcialmente resolvido, usando técnicas de resolução fácil e de dificuldade média; não é possível resolver mais quadrados usando-os. Para lhe dar uma boa oportunidade de detectar o peixe-espada, deve introduzir todas as marcas de lápis na grelha, como aqui mostrado.

Não há vias fáceis para detectar o padrão do peixe-espada. Assim, tente concentrar-se em apenas um número 1-9 à vez, enquanto digitaliza as suas marcas de lápis em filas e colunas. Olhe ao longo de cada uma das filas à vez, notando cada uma que contém apenas dois ou três quadrados com o número actual como uma possibilidade. Depois, procure ver se existem três filas onde os quadrados caem todos em três colunas. Se nada for encontrado, tente novamente com as colunas no lugar das linhas.

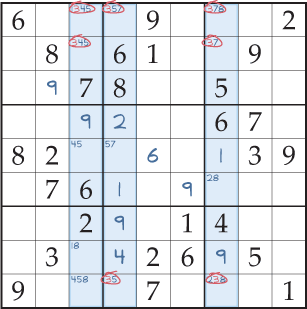Figure 4

Na Fig. 4, as marcas de lápis relevantes são introduzidas para mostrar que existem dois possíveis quadrados nos quais os 3 podem ser colocados na terceira e quarta colunas, e três possíveis quadrados na sétima coluna (destacados). Crucialmente, todos estes quadrados possíveis encontram-se em apenas três filas. Portanto, em cada uma das três linhas de intersecção, os 3 devem ser colocados numa das colunas destacadas. Assim, é possível eliminar a marca dos 3 lápis de todos os outros quadrados não resolvidos nestas linhas de interseção (Fig. 5). Estas eliminações, além disso, com uma intersecção coluna/bloco para remover uma marca de 7 lápis, deixam apenas uma marca de lápis no último quadrado da segunda linha, pelo que pode agora resolvê-lo para ser um 4.

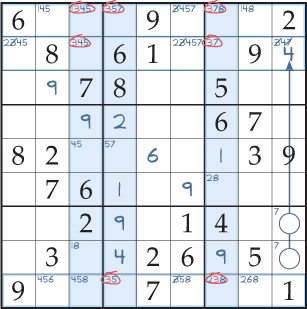Figure 5

Se gostar de jogar um Sudoku seriamente duro, experimente os puzzles no final do livro The Times Sudoku 6 com alguns que requerem a técnica do peixe-espada. Se gostas realmente de Super Fiendish, terás de esperar um pouco mais por The Times Sudoku 7 com 25 Sudoku extremamente duros, muitos dos quais precisam de asa x ou espadarte para completar.

Gerar um novo Sudoku