p>Conteúdo:
- O que é um Teste T?
- O Resultado T
- Valores T e Valores P
- Calculando o Teste T
- O que é um Teste T Parado (Amostras Paradas Teste T)?
O que é um Teste T?
>br>>>/p>
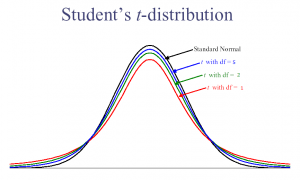p>Vários graus de liberdade para o T. O teste t diz-lhe quão significativas são as diferenças entre grupos; por outras palavras, permite-lhe saber se essas diferenças (medidas em meios) poderiam ter acontecido por acaso.
Um exemplo muito simples: Digamos que está constipado e que experimenta um remédio naturopático. A sua constipação dura alguns dias. Da próxima vez que tiver uma constipação, compra um medicamento de venda livre e a constipação dura uma semana. Faz um inquérito aos seus amigos e todos lhe dizem que as suas constipações tinham uma duração mais curta (uma média de 3 dias) quando tomaram o remédio homeopático. O que realmente quer saber é se estes resultados são repetíveis? Um teste t pode dizer-lhe, comparando os meios dos dois grupos e deixando-o saber a probabilidade de esses resultados acontecerem por acaso.
p>Outro exemplo: Os testes t de estudantes podem ser usados na vida real para comparar médias. Por exemplo, uma empresa farmacêutica pode querer testar um novo medicamento contra o cancro para descobrir se este melhora a esperança de vida. Numa experiência, há sempre um grupo de controlo (um grupo a quem é dado um placebo, ou “comprimido de açúcar”). O grupo de controlo pode mostrar uma esperança de vida média de +5 anos, enquanto que o grupo que toma o novo medicamento pode ter uma esperança de vida de +6 anos. Parece que o fármaco pode funcionar. Mas pode ser devido a uma casualidade. Para testar isto, os investigadores utilizariam um teste t de Estudante para descobrir se os resultados são repetíveis para toda uma população.
P>P>Tem problemas? Chegg.com irá corresponder-lhe com um tutor virtual (e os seus primeiros 30 minutos são grátis!).
A pontuação T.
A pontuação t é uma relação entre a diferença entre dois grupos e a diferença dentro dos grupos. Quanto maior for a pontuação t, mais diferença há entre os grupos. Quanto menor for a pontuação t, mais semelhança há entre os grupos. Uma pontuação t de 3 significa que os grupos são três vezes mais diferentes uns dos outros do que dentro uns dos outros. Quando se executa um teste t, quanto maior o valor t, maior a probabilidade de os resultados serem repetíveis.
- Uma pontuação t grande diz-lhe que os grupos são diferentes.
- Uma pontuação t pequena diz-lhe que os grupos são semelhantes.
Valores T e P
br>Quão grande é “suficientemente grande”? Cada valor t tem um valor p a acompanhar. Um valor p é a probabilidade de que os resultados dos seus dados de amostra ocorreram por acaso. Os valores de p são de 0% a 100%. São geralmente escritos como uma casa decimal. Por exemplo, um valor de p de 5% é 0,05. Os baixos valores de p são bons; indicam que os seus dados não ocorreram por acaso. Por exemplo, um valor p de .01 significa que existe apenas 1% de probabilidade de que os resultados de uma experiência tenham ocorrido por acaso. Na maioria dos casos, um valor p de 0,05 (5%) é aceite para significar que os dados são válidos.
Cálculo da Estatística / Tipos de Teste
br>Existem três tipos principais de teste t:
- Um teste t de amostras independentes compara os meios para dois grupos.
- Um teste t de amostra pareada compara as médias do mesmo grupo em momentos diferentes (digamos, com um ano de intervalo).
- Um teste t de amostra teste t t t t t testa a média de um único grupo contra uma média conhecida.
Provavelmente não quer calcular o teste à mão (a matemática pode ficar muito confusa, mas se insistir pode encontrar aqui os passos para um teste t de amostras independentes.
Utiliza as seguintes ferramentas para calcular o teste t:
Como fazer um teste T em Excel.
T teste em SPSS.
T distribuição na TI 89.
T distribuição na TI 83.
O que é um teste T emparelhado (Amostras emparelhadas Teste T / Amostras dependentes Teste T)?
Um teste t emparelhado (também chamado teste t de pares correlacionados, teste t de amostras emparelhadas ou teste t de amostras dependentes) é onde se executa um teste t em amostras dependentes. As amostras dependentes estão essencialmente ligadas – são testes sobre a mesma pessoa ou coisa. Por exemplo:
- Custos da RM do joelho em dois hospitais diferentes,
- Dois testes na mesma pessoa antes e depois do treino,
- Duas medições de tensão arterial na mesma pessoa utilizando equipamento diferente.
Quando escolher um teste T emparelhado / Amostras emparelhadas Teste T / Amostras dependentes Teste T
Escolha o teste T emparelhado se tiver duas medições sobre o mesmo item, pessoa ou coisa. Deve também escolher este teste se tiver dois itens que estão a ser medidos com uma condição única. Por exemplo, pode estar a medir o desempenho da segurança do automóvel na Pesquisa e Teste de Veículos e submeter os automóveis a uma série de testes de colisão. Embora os fabricantes sejam diferentes, poderá estar a sujeitá-los às mesmas condições.
Com um teste “regular” de duas amostras t, está a comparar os meios para duas amostras diferentes. Por exemplo, pode testar dois grupos diferentes de associados de serviço ao cliente num teste relacionado com negócios ou testar estudantes de duas universidades sobre os seus conhecimentos de inglês. Se tirar uma amostra aleatória de cada grupo separadamente e eles tiverem condições diferentes, as suas amostras são independentes e deve executar um teste t independente de amostras (também chamado entre amostras e amostras não pareadas).
A hipótese nula para o teste t independente de amostras é μ1 = μ2. Por outras palavras, assume que os meios são iguais. Com o teste t emparelhado, a hipótese nula é que a diferença de pares entre os dois testes é igual (H0: µd = 0). A diferença entre os dois testes é muito subtil; qual deles escolhe com base no seu método de recolha de dados.
Amostras emparelhadas Teste T À mão
P>Pergunta de amostra: Calcular um teste t emparelhado à mão para os seguintes dados: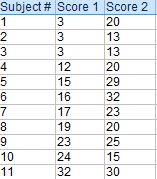
br>>>/p>p>P>Passo 1: Subtrair cada pontuação Y de cada pontuação X.
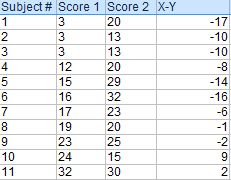br>
p>Passo 2: Somar todos os valores do Passo 1.
deixe este número de lado por um momento.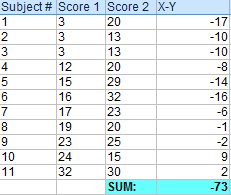
br>
P>Passo 3: Some todas as diferenças do Passo 1.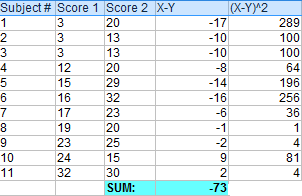
br>>
Passo 4: Some todas as diferenças ao quadrado do Passo 3.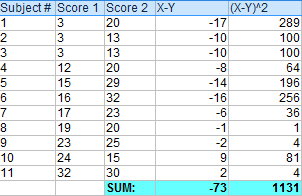
passo 5: Utilizar a seguinte fórmula para calcular o resultado t: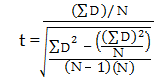
- ΣD: Soma das diferenças (soma de X-Y do Passo 2)
- ΣD2: Soma das diferenças ao quadrado (do Passo 4)
- (ΣD)2: Soma das diferenças (do Passo 2), ao quadrado.
Se não estiver familiarizado com Σ, talvez queira ler primeiro sobre a notação de soma.
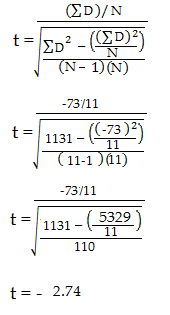
P> Passo 6: Subtrair 1 do tamanho da amostra para obter os graus de liberdade. Temos 11 itens, portanto 11-1 = 10.
passo 7: Encontrar o valor p na tabela t, utilizando os graus de liberdade no passo 6. Se não tiver um nível alfa especificado, use 0,05 (5%). Para este problema de exemplo, com df = 10, o valor t é 2,228.
P>Passo 8: Compare o valor da sua tabela t do Passo 7 (2,228) com o seu valor t calculado (-2,74). O valor t calculado é maior que o valor da tabela a um nível alfa de .05. O valor p é inferior ao nível alfa: p <.05. Podemos rejeitar a hipótese nula de não haver diferença entre médias.
Nota: Pode-se ignorar o sinal menos ao comparar os dois valores t, como ± indica a direcção; o valor p permanece o mesmo para ambas as direcções.
Verifica o nosso canal YouTube para mais ajuda e dicas sobre estatísticas!
Goulden, C. H. Methods of Statistical Analysis, 2ª ed. New York: Wiley, pp. 50-55, 1956.
div> CITE ESTE AS:
Stephanie Glen. “Teste T” (Teste T do Estudante): Definição e Exemplos” de StatisticsHowTo.com: Estatísticas Elementares para o resto de nós! https://www.statisticshowto.com/probability-and-statistics/t-test/ ——————————————————————————
p>Need help with a homework or test question? Com o Chegg Study, pode obter soluções passo a passo para as suas perguntas de um especialista na matéria. Os seus primeiros 30 minutos com um tutor do Chegg são gratuitos!